边分治学习笔记(bzoj2870)
如果点分治的话,那个取最小点权操作很难合并,不过树可以点分治,那自然也可以边分治。我们每次找到一条边,使得删掉这条边后的两个连通块中最大的那个的大小尽可能小,然后处理经过这条边的路径信息……
桥豆麻袋,这个复杂度好像不太对啊。
在菊花图上,好像可以轻易变成 O(n) O ( n ) 的啊!!!
于是我们就要把树做一下转化,如果一个点有太多个儿子,我们就建立若干个虚拟点来管理它的儿子们,这样这棵树就变成了二叉树,可以保证 O(nlogn) O ( n l o g n )
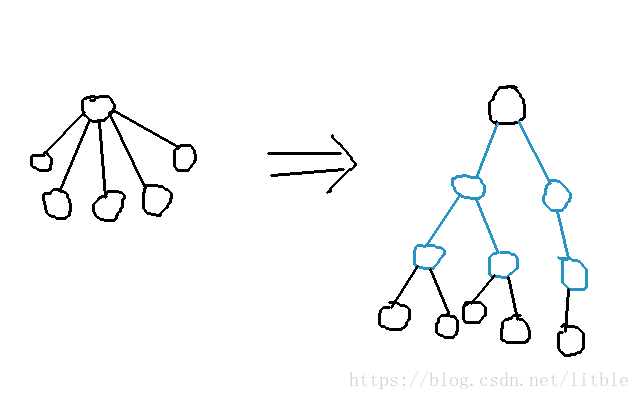
我们发现,只要把虚拟点的点权设为原来那个父亲的点权,就不会影响找点权最小值的操作。但是找链条的长度的话,如果两个点的LCA是一个虚拟点的话,它们真实的父亲的贡献就不会被计算。所以我们令真实边的边权为1,虚拟边边权为0,那么一条链的长度就是这条链边权和+1。
这样就好办多了,每次我们找到一条边,使得删掉这条边后的两个连通块中最大的那个的大小尽可能小,然后把边两端的路径存下来,按照点权最小值排序,然后对于A端的一条路径,我们维护B端点权大于等于该路径的路径中,长度最长的一条,对B端也这么做一边就可以得到答案。复杂度 O(nlog2n) O ( n l o g 2 n )
至于空间,我们知道线段树要开四倍空间,所以对于菊花图,这个重建树就也是四倍空间。
#includeelse {
int o1=++n,o2=++n;v[o1]=v[o2]=v[i];
add(i,o1,0),add(o1,i,0),add(i,o2,0),add(o2,i,0);
for(RI j=0;jif(j&1) a[o2].push_back(a[i][j]);
else a[o1].push_back(a[i][j]);
}
}
}
void getrt(int x,int las,int SZ) {
sz[x]=1;
for(RI i=h[x];i;i=ne[i]) {
if(vis[i>>1]||to[i]==las) continue;
getrt(to[i],x,SZ),sz[x]+=sz[to[i]];
int kl=max(sz[to[i]],SZ-sz[to[i]]);
if(klvoid dfs2(int o,int x,int las,int len,int val) {
val=min(val,v[x]),t[o][++js[o]]=(node){val,len};
for(RI i=h[x];i;i=ne[i]) {
if(vis[i>>1]||to[i]==las) continue;
dfs2(o,to[i],x,len+d[i],val);
}
}
void work(int x,int SZ) {
mxx=inf,getrt(x,0,SZ);
if(mxx==inf) return;
int now=rt;vis[now>>1]=1;
js[0]=js[1]=0,dfs2(0,to[now],0,0,inf),dfs2(1,to[now^1],0,0,inf);
sort(t[0]+1,t[0]+js[0]+1,cmp),sort(t[1]+1,t[1]+js[1]+1,cmp);
for(RI i=1,j=1,mxl=0;i<=js[0];++i) {
while(j<=js[1]&&t[1][j].v>=t[0][i].v) mxl=max(mxl,t[1][j].len),++j;
if(j!=1) ans=max(ans,1LL*t[0][i].v*(mxl+t[0][i].len+d[now]+1));
}
for(RI i=1,j=1,mxl=0;i<=js[1];++i) {
while(j<=js[0]&&t[0][j].v>=t[1][i].v) mxl=max(mxl,t[0][j].len),++j;
if(j!=1) ans=max(ans,1LL*t[1][i].v*(mxl+t[1][i].len+d[now]+1));
}
int ksz=sz[to[now]];work(to[now],ksz),work(to[now^1],SZ-ksz);
}
int main()
{
int x,y;
n=kn=read();
for(RI i=1;i<=n;++i) v[i]=read();
for(RI i=1;i1),add(y,x,1);
dfs1(1,0),rebuild(),work(1,n);
printf("%lld",ans);
return 0;
}