图的邻接矩阵 (图的遍历、Prim算法、Dijkstra算法、Floyd算法)
图的邻接矩阵 (图的遍历、Prim算法、Dijkstra算法、Floyd算法)
一、源代码
1、邻接矩阵的数据结构
#include2、基本操作
创建邻接矩阵、销毁邻接矩阵、返回顶点v的第一个邻接顶点、返回邻接矩阵的下一个邻接顶点
//创建邻接矩阵
void CreatGraph(MGraph* Graph){
printf("输入顶点数:");
scanf("%d",&Graph->vexnum);
printf("输入弧数:");
scanf("%d",&Graph->arcnum);
Graph->arcs=(ArcCell**)malloc((Graph->vexnum+1)*sizeof(ArcCell*)); //动态开辟二维数组,0号单元不用
Graph->info=(int*)malloc((Graph->vexnum+1)*sizeof(int));
for(int i=0;i<=Graph->vexnum;i++)
Graph->arcs[i]=(ArcCell*)malloc((Graph->vexnum+1)*sizeof(ArcCell));
for(int i=0;i<=Graph->vexnum;i++)
for(int j=0;j<=Graph->vexnum;j++)
Graph->arcs[i][j]=0; //邻接矩阵全部置0,初始化
for(int i=1;i<=Graph->vexnum;i++){ //开始输入
int j;
printf("输入顶点信息");
scanf("%d",&Graph->info[i]);
printf("输入与%d顶点邻接的节点",i);
scanf("%d",&j);
while(j!=-1){
printf("输入%d到%d的权重",i,j);
scanf("%d",&Graph->arcs[i][j]);
printf("输入与%d邻接的下一个节点",i);
scanf("%d",&j);
}
}
}
//销毁邻接矩阵
void ClearGraph_M(MGraph *G)
{
(*G).vexnum = 0;
(*G).arcnum = 0;
}
//获得邻接矩阵的某个顶点
int GetVex_M(MGraph G, int order)
{
if(order>=1 && order<=G.vexnum)
return G.info[order];
else
return -1;
}
//返回顶点v的第一个邻接顶点
int FirstAdjVex_M(MGraph G,int v)
{
for(int i=1;i<=G.vexnum;i++)
if(G.arcs[v][i]!=0)
return i;
return -1;
}
//返回邻接矩阵的下一个邻接顶点
int NextAdjVex_M(MGraph G, int v, int w) //v是顶点,w是当前顶点连接的顶点
{
for(int i=w+1;i<=G.vexnum;i++)
if(G.arcs[v][i]!=0)
return i;
return -1;
}
3、图的遍历
//深度优先遍历
int visited[100]; //标志数组,0表示未被访问,1表示已访问
void DFS(MGraph G,int v);
void DFSTraverse(MGraph G){ //对图G做深度优先遍历
int v;
for(v=1;v<=G.vexnum;v++) //标志数组初始化
visited[v]=0;
for(v=1;v<=G.vexnum;v++)
if(!visited[v]) DFS(G,v);
}
void DFS(MGraph G,int v){
//从第v个顶点出发递归地深度优先遍历图G
int w;
visited[v]=1;
printf("%d",G.info[v]); //访问第v个顶点
for(w=FirstAdjVex_M(G,v);w!=-1;w=NextAdjVex_M(G,v,w))
if(!visited[w]) DFS(G,w); //对v的尚未访问的邻接顶点w递归调用DFS
}
//广度优先遍历算法
void BFSTraverse(MGraph G){
//按广度优先非递归遍历图G,使用辅助队列Q和标志访问数组
int v;
for(v=1;v<=G.vexnum;v++) //标志数组初始化
visited[v]=0;
queue<int> Q; //辅助队列
for(v=1;v<=G.vexnum;v++){
if(!visited[v]){
visited[v]=1;
printf("%d",G.info[v]);
Q.push(v);
while(!Q.empty()){
int u=Q.front(); //队头元素出队并置位 Q
Q.pop();
for(int w=FirstAdjVex_M(G,u);w!=-1;w=NextAdjVex_M(G,u,w)){
if(!visited[w]){ //w为u的尚未访问的邻接顶点
visited[w]=1;
printf("%d",G.info[w]);
Q.push(w);
}
}
}
}
}
}
4、生成树(prim算法)
//无向图的连通分量和生成树(深度优先生成树)
typedef struct CS{
int data;
struct CS *firstchild,*nextsibling;
}CSNode,*CSTree;
void DFSTree(MGraph G,int v,CSTree *T);
void DFSForest(MGraph G,CSTree *T,int *c){
//建立无向图G的深度优先生成森林的孩子兄弟链表
*T= nullptr;
CSTree p,q;
q=(CSTree)malloc(sizeof(CSNode));
int v,count=0; //count为连通分量个数
for(v=1;v<=G.vexnum;v++) //标志数组初始化
visited[v]=0;
for(v=1;v<=G.vexnum;v++)
if(!visited[v]){ //第V个顶点为新的生成树的根节点
p=(CSTree)malloc(sizeof(CSNode)); //分配根节点
p->data=GetVex_M(G,v); //给根节点赋值
p->firstchild=nullptr;
p->nextsibling=nullptr;
if(!(*T))
(*T)=p; //是第一棵生成树的根
else q->nextsibling=p; //是其他生成树的根(前一棵根的兄弟)
q=p; //q指示当前生成树的树根
DFSTree(G,v,&p); //建立以p为根的生成树
count++;
}
*c=count;
}
void DFSTree(MGraph G,int v,CSTree *T){
//从第v个顶点出发深度优先遍历图G,建立以T为根的生成树
CSTree p,q;
int first=1;
visited[v]=1;
for(int w=FirstAdjVex_M(G,v);w!=-1;w=NextAdjVex_M(G,v,w)){
if(!visited[w]){
p=(CSTree)malloc(sizeof(CSNode)); //分配孩子节点
p->data=GetVex_M(G,w);
p->nextsibling=nullptr;
p->firstchild=nullptr;
if(first){ //w是v的第一个未被访问的邻接顶点
(*T)->firstchild=p; //是根的左孩子结点
first=0;
}else{ //w是v的其他未被访问过的邻接顶点
q->nextsibling=p; //是上一邻接顶点的右兄弟结点
}
q=p;
DFSTree(G,w,&q); //从第w个顶点出发深度优先遍历图G,建立子生成树
}
}
}
//验证生成树
void LevelTraverse(CSTree T) { //孩子兄弟链表的层次遍历算法
CSTree P = T;
CSTree K ;
queue<CSTree> sqQueue; //声明一个队列
while (P) //这里的 P 是指森林中可能有多棵子树,指向每棵子树的根节点
{
K = P; //利用 K 来遍历以 P 为根节点子树中的节点
sqQueue.push(K); //先将根节点入队
while (!sqQueue.empty()) { //只要队列不为空,则依次出队,直到队空
printf("%d",sqQueue.front()->data); //打印该元素
K=sqQueue.front();
sqQueue.pop(); //出队
if (K->firstchild) { //如果该节点不是森林中的叶节点,则进入下一层
K = K->firstchild; //将 K 指向 K 最左边的孩子
sqQueue.push(K); //入队
while (K->nextsibling) { //判断它是否有兄弟节点
K = K->nextsibling;
sqQueue.push(K);;//入队它的兄弟节点(在同一层上)
}
}
}
P = P->nextsibling; //指向下一棵树的根节点
}
}
//Prim算法
//记录从顶点集U到V-U的代价最小边的辅助数组的定义
typedef struct close{
int adj_vex;
int low_cost;
}close;
int minimum(close closeage[100],int vexnum);
void MiniSpanTree_Prim(MGraph G,int u){
//从第u个顶点出发构造网G的最小生成树T,输出T的各条边
//记录从顶点集U到V-U的代价最小边的辅助数组的定义
close closedge[100];
int k=u;
for(int j=0;j<=G.vexnum;j++) { //辅助数组初始化
if (j != k) {
closedge[j].adj_vex = k; //初始顶点集只有一个
if (G.arcs[k][j] != 0)
closedge[j].low_cost = G.arcs[k][j]; //存放u到各边的权值
else closedge[j].low_cost = -1; //-1表示不可到达
}
}
closedge[k].low_cost=0; //到自身的代价为0
closedge[k].adj_vex=k;
for(int i=2;i<=G.vexnum;i++){ //选择其余的G.vexnum-1个顶点
k=minimum(closedge,G.vexnum); //求出T的下一个节点,第k个节点
printf("%d->%d ",closedge[k].adj_vex,G.info[k]); //输出生成树的边
closedge[k].low_cost=0; //第k顶点并入u集
for(int j=1;j<=G.vexnum;j++){
if((G.arcs[k][j]<closedge[j].low_cost&&closedge[j].low_cost>0&&G.arcs[k][j]>0)||closedge[j].low_cost==-1) { //新顶点并入后重新选择最小边
closedge[j].adj_vex = G.info[k];
closedge[j].low_cost=G.arcs[k][j];
}
}
}
}
int minimum(close closedge[100],int vexnum){
int min=100;
int i,k=1;
for(i=1;i<=vexnum;i++){
if(closedge[i].low_cost<min&&closedge[i].low_cost>0){
min=closedge[i].low_cost;
k=i;
}
}
return k; //返回T的下一个节点,权重最小的那个
}
5、Dijkstra算法(从某个源点到其余各顶点的最短路径)
//Dijkstra算法(从某个源点到其余各顶点的最短路径)
/* 最短路径类型定义 */
#define INF 10000 //定义无穷大
void Dijkstra(MGraph G, int v0)
{
int set[G.vexnum+1];
int min,i,j,v;
int tmp[G.vexnum+1],k;
int path1[G.vexnum+1]; //path[i]表示从源点到顶点i之间最短路径的前驱节点
int dist1[G.vexnum+1]; //记录源点到顶点i之间的最短路径长度,dist的初值为arcs[v0][i]
for(i=1;i<=G.vexnum;i++){//数组初始化
if(G.arcs[v0][i])
dist1[i]=G.arcs[v0][i]; //dist1[i]:v0到i的最短路径长度
else dist1[i]=INF; //dist为无穷大
set[i]=0; //set[i]:标记数组,标记各顶点是否已加入路径
if(G.arcs[v0][i])
path1[i]=v0; //path1[i]:保存从v0到vi路径上vi的前一个顶点
else
path1[i]=-1; //代表v0到vi中间不经过任何顶点(可能不通,也可能是自身)
}
set[v0]=1;
path1[v0]=-1;
for(i=1;i<=G.vexnum;i++){ //初始化结束,关键操作开始(判断其余G1.vexnum-1个顶点)
min=10000;
for(j=1;j<=G.vexnum;j++){ //选出v0到剩余顶点中最短的一条路径
if(!set[j] && dist1[j]<min){
v=j;
min = dist1[j]; //v0到剩余顶点的最短路径6、Floyd算法求各顶点之间最短路径
//Floyd算法求各顶点之间最短路径
void Floyd(MGraph G)
{
int i, j, k;
int path[10][G.vexnum+1];
int dist[10][G.vexnum+1];
int tmp[G.vexnum+1];
for(i=1;i<=G.vexnum;i++){ //赋初值
for(j=1; j<=G.vexnum; j++){
if(G.arcs[i][j])
dist[i][j] = G.arcs[i][j];
else dist[i][j]=INF;
path[i][j] = -1;
}
}
for(k=1;k<=G.vexnum;k++){ //以k为中间点检测各对顶点间距离
for(i=1;i<=G.vexnum;i++){
for(j=1;j<=G.vexnum;j++){
if(i!=j && dist[i][k]!=INF && dist[k][j]<INF && dist[i][k]+dist[k][j]<dist[i][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = k;
}
}
}
}
//输出各对顶点之间路径
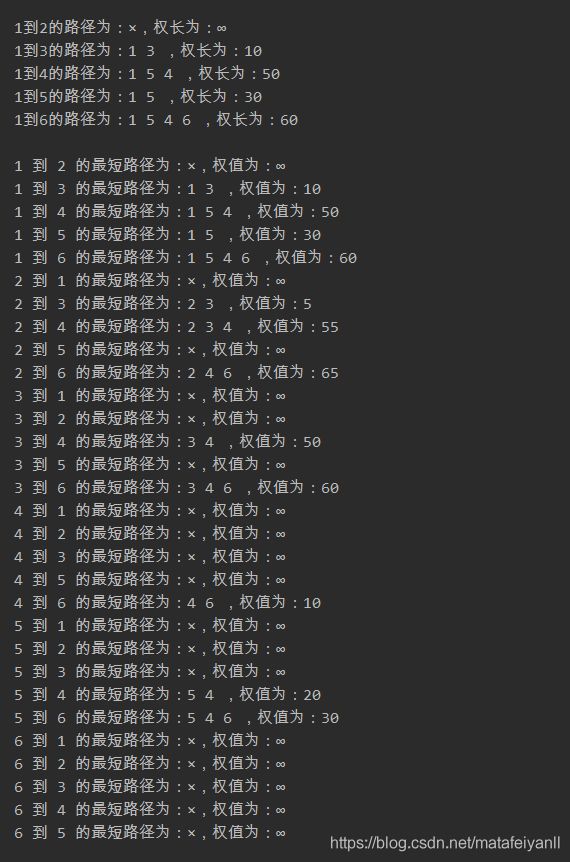
for(i=1;i<=G.vexnum;i++){
for(j=1; j<=G.vexnum; j++){
if(i!=j){
printf("%d 到 %d 的最短路径为:", G.info[i], G.info[j]);
if(dist[i][j]!=INF){
printf("%d ", G.info[i]);
k = i;
while(path[k][j]!=-1){
printf("%d ", G.info[path[k][j]]);
k = path[k][j];
}
printf("%d ", G.info[j]);
}
else
printf("×");
printf(",权值为:");
if(dist[i][j]==INF)
printf("∞\n");
else
printf("%d\n", dist[i][j]);
}
}
}
}
二、图解
三、测试
1、测试函数
//测试函数
int main()
{
MGraph G;
CreatGraph(&G);
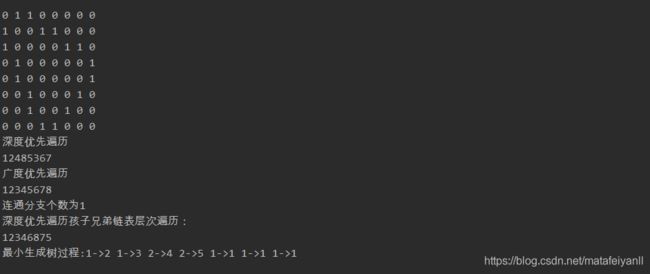
printf("邻接矩阵:\n");
for(int i=1;i<=G.vexnum;i++) {
printf("\n");
for (int j = 1; j <= G.vexnum; j++)
printf("%d ", G.arcs[i][j]);
}
printf("\n");
printf("深度优先遍历\n");
DFSTraverse(G);
printf("\n");
printf("广度优先遍历\n");
BFSTraverse(G);
CSTree T;
int count;
DFSForest(G,&T,&count);
printf("\n");
printf("连通分支个数为%d\n",count);
printf("深度优先遍历孩子兄弟链表层次遍历:\n");
LevelTraverse(T);
printf("\n");
printf("最小生成树过程:");
MiniSpanTree_Prim(G,1);
printf("\n");\
printf("\n");
Dijkstra(G,1);
printf("\n");
Floyd(G);
return 0;
}
//测试数据1 p168 8 9 1 2 1 3 1 -1 2 1 1 4 1 5 1 -1 3 1 1 6 1 7 1 -1 4 2 1 8 1 -1 5 2 1 8 1 -1 6 3 1 7 1 -1 7 3 1 6 1 -1 8 4 1 5 1 -1
//测试数据2 p174 6 10 1 2 6 3 1 4 5 -1 2 1 6 3 5 5 3 -1 3 1 1 2 5 4 5 5 6 6 4 -1 4 1 5 3 5 6 2 -1 5 2 3 3 6 6 6 -1 6 3 4 4 2 5 6 -1
//测试数据3 p188 6 8 1 3 10 5 30 6 100 -1 2 3 5 -1 3 4 50 -1 4 6 10 -1 5 4 20 6 60 -1 6 -1