sklearn库LDA进行图片数据降维

1.简介

     在另一篇文章中讲了利用PCA对图片数据进行降维，这次介绍一下另一种降维方法——LDA(Linear Discriminant Analysis)，即线性判别分析。跟PCA不同，LDA是一种supervised的降维方法。即我们对数据降维时需要数据的label。

    LDA的原理是要找到一个投影面，使得投影后相同类别的数据点尽可能的靠在一起，而不同类别的数据点尽可能的分开。说白了就是同一类别的点方差尽可能大，而各类别数据的平均值相互之间的距离尽可能的大。想要了解具体的计算过程的朋友可以上知乎去看看相关的讲解。了解原理对函数的使用会有很大的帮助。

 

2.数据降维

     同样这次使用的数据集是一些图片像素点数据，每个图片的数字是0,1,2,3或者4。每张图片由28×28=764个像素点组成，每个像素点大小在0-255之间。所以我们的每个数据都是764维的。在这里将其降至2维。

    同样，要对数据进行降维有两种方法，代码如下。其中方法2是用原数据与LDA.scalings_相乘获得。LDA.scalings_即计算后获得的降维方向的向量组成的矩阵。这里跟PCA第二种降维方法类似。

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

#读取数据
df = pd.read_csv('DataB.csv',index_col=0)
output = df['gnd']   #属性'gnd'即数据的label
df = df.drop('gnd',axis=1)


#方法1，调用时直接指定n_components的大小，然后转换。
LDA = LinearDiscriminantAnalysis(n_components=2)
LDA_1_2 = LDA.fit_transform(df,output)



#方法2：调用LDA时不指定n_components的大小。然后利用用原数据与LDA.scalings_相乘获得降维后的数据。
LDA = LinearDiscriminantAnalysis()
LDA.fit(df,output)
LDA_1_2 = pd.DataFrame(np.dot(df,LDA.scalings_[:,0:2]))

3.效果展示

     将原数据降至2维后，利用这两个维度的数据作图，并且根据不同类别进行分类，代码如下:

LDA_1_2 = pd.DataFrame(np.dot(df,LDA.scalings_[:,0:2]))
LDA_1_2['category'] = output.values 
sns.set(rc={'figure.figsize':(11,8)})
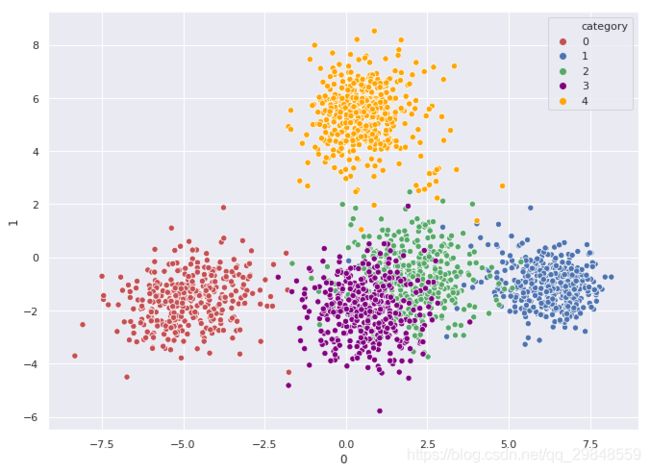
ax = sns.scatterplot(data=LDA_1_2,x=0,y=1,hue='category',s=40,palette={0:'r',1:'b',2:'g',3:'purple',4:'orange'})

     作得的图如下。可以看的出不同数据的数据点互相是分开的。而数字2和数字3的因为本身长得类似，所以数据点有一定重合。这个降维的效果可以说相当出色，保留了原数据的大量信息，便于观察。

 

4.LDA与PCA对比

     分别利用LDA和PCA将数据降至四维，然后将降维后的数据分为训练集和测试集。利用训练集训练贝叶斯分类器，再对测试集的数据进行分类。代码如下:

from sklearn.naive_bayes import GaussianNB

df_bc = pd.read_csv('DataB.csv',index_col=0)
output = df_bc['gnd'].values


lda = LinearDiscriminantAnalysis(n_components=4)
lda_array = pd.DataFrame(lda.fit_transform(df_bc.drop('gnd',axis=1),output))

pca = PCA(n_components=4)
pca_array = pd.DataFrame(pca.fit_transform(df_bc.drop('gnd',axis=1)))


LDA = []
pCA = []
 

for i in range(10):
    LDA_train,LDA_test,PCA_train,PCA_test,y_train,y_test = train_test_split(lda_array,pca_array,df_bc['gnd'],test_size=0.3,random_state=i)
    bc =  GaussianNB()
    bc.fit(LDA_train,y_train)
    LDA.append(bc.score(LDA_test,y_test))
    bc.fit(PCA_train,y_train)
    pCA.append(bc.score(PCA_test,y_test))

print('LDA:',np.mean(LDA))
print('PCA:',np.mean(pCA))

    计算得到准确率为:

LDA: 0.9932258064516128
PCA: 0.8348387096774192

    可以看出LDA的准确率是相当高的，这说明LDA降维后的数据因为有label的存在，因此能够使得不同类别的数据相互分隔开来。说明在有label的情况下使用LDA降维是一个不错的选择。而在这里PCA降维的准确率较低，但是如果我们增加维度数的话，准确率可以增大到95%以上。这是因为每一维都蕴藏着原数据的信息，因此所用的维度多的话更能反应原数据的特性。

    另外的降维数据还有LLE和MDS还有ISOMAP等，它们各有各的特点。以后有空会一一介绍。