【小白学图像】Group Normalization详解+PyTorch代码

文章转自公众号【机器学习炼丹术】，关注回复“炼丹”即可获得海量免费学习资料哦！

---

总的来说，GN是对BN的改进，是IN和LN的均衡。

1 BN的优点

这里简单的介绍一下BN，在之前的文章中已经详细的介绍了BN算法和过程。

BN于2015年由 Google 提出，Google在ICML论文中描述的非常清晰，即在每次SGD时，通过mini-batch来对相应的activation做规范化操作，使得结果（输出信号各个维度）的均值为0，方差为1。最后的“scale and shift”操作则是为了训练所需而“刻意”加入的BN能够有可能还原最初的输入，从而保证数据中有用信息的留存。

【BN的好处】

1. BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度；

2. BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定；

3. BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题；

4. BN具有一定的正则化效果。

2 BN的缺点

2.1 受限于Batch size

BN 沿着 batch 维度进行归一化，其受限于 Batch Size，当 Batch Size 很小时，BN 会得到不准确的统计估计，会导致模型误差明显增加

【一般每块 GPU 上 Batch Size =32 最合适。】

但对于目标检测，语义分割，视频场景等，输入图像尺寸比较大，而限于GPU显卡的显存限制，导致无法设置较大的 Batch Size，如 经典的Faster-RCNN、Mask R-CNN 网络中，由于图像的分辨率较大，Batch Size 只能是 1 或 2.

2.2 训练集与测试集的分布

BN处理训练集的时候，采用的均值和方差是整个训练集的计算出来的均值和方差 （这一部分没有看懂的话，可能需要去看一下BN算法的详解）

所以测试和训练的数据分布如果存在差异，那么就会导致训练和测试之间存在不一致现象（Inconsistency）。

3 Group Normalzation

Group Normalization(GN)是由2018年3月份何恺明团队提出，GN优化了BN在比较小的mini-batch情况下表现不太好的劣势。

Group Normalization(GN) 则是提出的一种 BN 的替代方法，其是首先将 Channels 划分为多个 groups，再计算每个 group 内的均值和方法，以进行归一化。 GB的计算与Batch Size无关，因此对于高精度图片小BatchSize的情况也是非常稳定的，

下图是比较BN和GN在Batch Size越来越小的变化中，模型错误率变化的对比图：

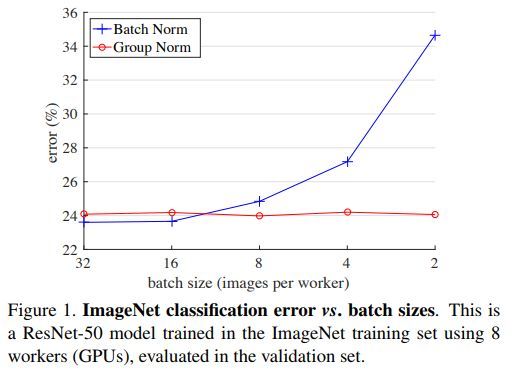
因此在实验的时候，可以在尝试使用GN来代替BN哦~

其实不难发现，GN和LN是存在一定的关系的。

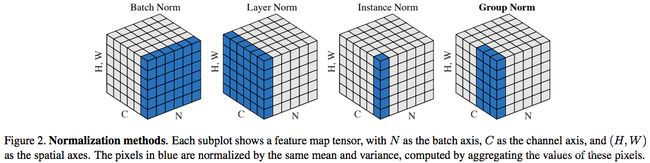
上图中有四种Normalization的方法。就先从最简单的Instance Normalization开始分析：

• IN：仅仅对每一个图片的每一个通道最归一化。也就是说，对【H，W】维度做归一化。假设一个特征图有10个通道，那么就会得到10个均值和10个方差；要是一个batch有5个样本，每个样本有10个通道，那么IN总共会计算出50个均值方差；
• LN：对一个特征图的所有通道做归一化。5个10通道的特征图，LN会给出5个均值方差；
• GN：这个是介于LN和IN之间的一种方法。假设Group分成2个，那么10个通道就会被分成5和5两组。然后5个10通道特征图会计算出10个均值方差。
• BN:这个就是对Batch维度进行计算。所以假设5个100通道的特征图的话，就会计算出100个均值方差。5个batch中每一个通道就会计算出来一个均值方差。

在GN的论文中，给出了GN推荐的group Number：

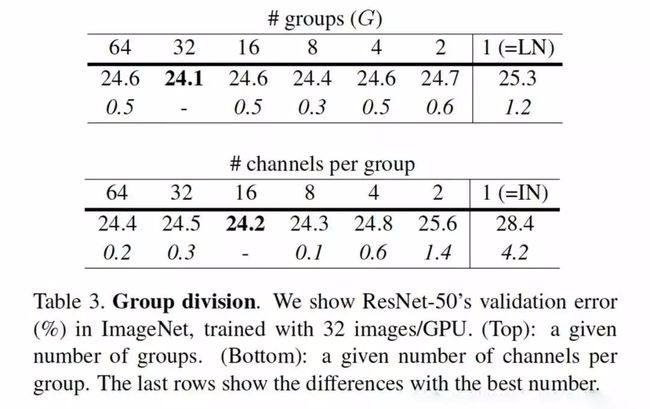
• 第一个表格展示GN的group Number不断减小，退化成LN的过程。其实，分组32个group效果最好；
• 第二个表格展示GN的每一组的channel数目不断减小，退化成IN的过程。每一组16个channel的效果最好 ，我个人在项目中也会有优先尝试16个通道为一组的这种参数设置。

4 PyTorch实现GN

import numpy as np
import torch
import torch.nn as nn


class GroupNorm(nn.Module):
    def __init__(self, num_features, num_groups=32, eps=1e-5):
        super(GroupNorm, self).__init__()
        self.weight = nn.Parameter(torch.ones(1,num_features,1,1))
        self.bias = nn.Parameter(torch.zeros(1,num_features,1,1))
        self.num_groups = num_groups
        self.eps = eps

    def forward(self, x):
        N,C,H,W = x.size()
        G = self.num_groups
        assert C % G == 0

        x = x.view(N,G,-1)
        mean = x.mean(-1, keepdim=True)
        var = x.var(-1, keepdim=True)

        x = (x-mean) / (var+self.eps).sqrt()
        x = x.view(N,C,H,W)

当然，你要是想问PyTorch是否已经集成了GN？那必然的。下面的代码比较了PyTorch集成的GN和我们手算的GN的结果。

import torch
import torch.nn as nn

x=torch.randn([2,10,3,3])+1
# Torch集成的方法
m=torch.nn.GroupNorm(num_channels=10,num_groups=2)

# 先计算前面五个通道的均值
firstDimenMean = torch.Tensor.mean(x[0,0:5])
# 先计算前面五个通道的方差
firstDimenVar= torch.Tensor.var(x[0,0:5],False)
# 减去均值乘方差
y2 = ((x[0][0][0][1] - firstDimenMean)/(torch.pow(firstDimenVar+m.eps,0.5) )) * m.weight[0] + m.bias[0]
print(y2)

y1=m(x)
print(m.weight)
print(m.bias)
print(y1[0,0,0,1])

输出结果：

tensor(0.4595, grad_fn=<AddBackward0>)
Parameter containing:
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.], requires_grad=True)
Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], requires_grad=True)
tensor(0.4595, grad_fn=<SelectBackward>)