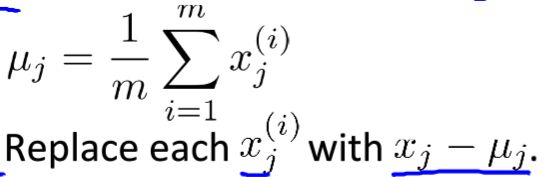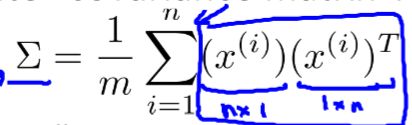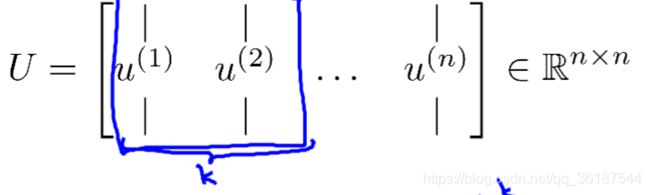机器学习(8)--PCA算法及python中sklearn模块实现
吴恩达ML课程课后总结,以供复习、总结、温故知新,也欢迎诸位评论讨论分享,一起探讨一起进步:
上一篇:机器学习(7)--K均值算法及python实现(附练习数据资源文件百度云)https://blog.csdn.net/qq_36187544/article/details/88381370
下一篇:机器学习(9)--异常检测(多元高斯分布等)https://blog.csdn.net/qq_36187544/article/details/88400810
当特征数量很大时,可能就有特征代表的含义冗杂,如果特征高度相关,就需要进行降维。(不局限于无监督学习,在监督学习中同样可以运用)
降维可以对数据进行压缩,节省内存,也可让数据可视化。(说白了,降维的目的就是为了加快运行速度节省内存,但是会损失一定的数据信息,因为只能可视化展示1,2,3维数据,高维不能展示所以把高维的降成低维的就可以展示了)
降维的最最基本思想就是采用投影的方式。PCA(principal components analysis)主成分分析是降维采用的算法之一。
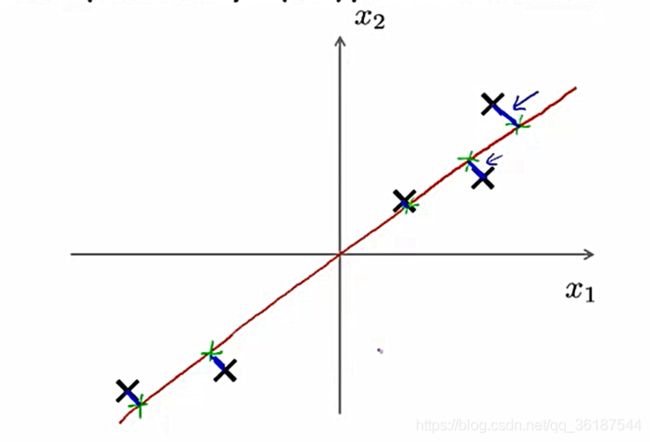
PCA主成分分析算法:找到一个低维平面(二维转一维问题中就是直线)使各数据到低维平面的正交(垂直)距离平方最小,这个距离也称为投影误差。(举例如下图,二维转一维,找到一条直线使点到直线的正交距离蓝色线段最短,投影误差最小)
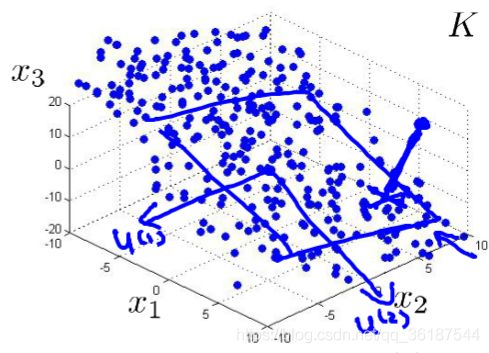
N维转N-1维即找到N-1个向量构成向量子空间,进行降维(如下图,三维转二维,得到两个u(1),u(2)向量构成向量子空间,这里是一个平面作为降维结果)
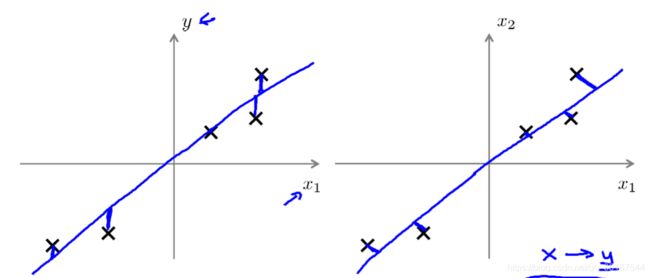
PS:与线性回归的差别,下左图为线性回归,纵坐标为y,计算的是实际的点与计算的点的差值即y坐标差值,下右图为PCA,计算的是点到低维空间(由于2维转一维,所以是直线)正交长度即投影误差的长。
在进行PCA算法时一般先进行特征缩放(下图是一种特征缩放的方式,计算均值再把xj换成xj-均值,当然也可以用统计量x-μ/s进行特征缩放,只是在使用验证集时别忘了同样要缩放哦),进行协方差矩阵计算就能找到对应的N-1个向量子空间向量
协方差矩阵计算,Σ是协方差矩阵,不是求和:
主流编程语言都有库函数来计算矩阵U(矩阵U由u(1),u(2)组成,就是向量子空间的对应向量),若要缩放成K维就取前K列即可。
简单描述其他资料协方差的理解:PCA的目的就是“降噪”(噪声是干扰,比如与真实相差很多的数据,不符合实际情况,方差越小噪声越小)和“去冗余”(某些维度相关性强,冗余)。协方差矩阵度量的是维度与维度之间的关系,以两个特征为例,COV(X,Y),若协方差为正则正相关,为负则负相关,为0则独立,利用这一点性质进行去冗杂。协方差矩阵的主对角线上的元素是各个维度上的方差,让保留下的不同维度间的相关性尽可能小,也就是说让协方差矩阵中非对角线元素都基本为零。
上面提到过k(高维降成k维)主成分数量的选择:看方差保留百分比,方差表示的是相关信息
算法:从k=1开始计算方差保留百分比,达标即可
应用建议:训练集得到Ureduce,在测试集或者验证集时要记得对应变换(等同于特征缩放时训练集缩放,测试集同样的)
PCA不适用于防止过拟合,因为会损失方差信息,尽管很少,但有可能损失有价值的信息,过拟合推荐正则化
做计划时不要把PCA考虑在内,因为PCA的作用是数据压缩和可视化,除非内存不足够支撑或者速度太慢,一般都先采用直接使用原始数据进行算法训练,毕竟PCA会损失方差信息。
因为PCA算法适用于任何算法的前置数据处理,本来是准备放在神经网络或者SVM算法前进行PCA处理后再看一下结果,但合计了一下,PCA算法只提供加速和减少内存的功能并不能对运行结果有所影响(降维降的太狠结果会更差),所以就不采用PCA算法练习了,这里稍微说明下python中使用sklearn模块对PCA算法的运用:
官网实例,将二维数据降为一维数据:
参数n_components表示保留的特征数,默认为1。如果设置成‘mle’,那么会自动确定保留的特征数
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> pca = PCA(n_components=2) # 自动设置参数可这样写:pca=PCA(n_components='mle')
>>> pca.fit(X)
PCA(copy=True, n_components=2, whiten=False)
>>> print(pca.explained_variance_ratio_)
[ 0.99244... 0.00755...]