【LeetCode】99.恢复二叉搜索树
文章目录
- 1.思想
- 2.题目
- 3.代码
- 4.语法知识补充
1.思想
(1)什么是二叉搜索树?
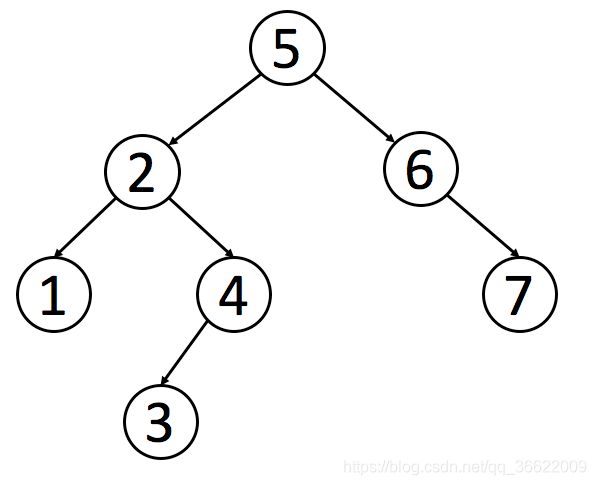
二叉搜索树(Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。如下就是一个符合定义的 BST:
不能单纯地判断根是否比左孩子大,比右孩子小,如果是下面这种情况,就会产生误判:根比右孩子的右孩子大。

正确的做法是,假设根是左子树上的最大值,且是右子树上的最小值,如果左子树或者右子树不满足这个条件,那么就不合法。
boolean isValidBST(TreeNode root) {
//初始条件:min和max都为空,不用判断root的合法性
return isValidBST(root, null, null);
}
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
if (root == null) return true;
//此节点的值应该比min的值大
if (min != null && root.val <= min.val) return false;
//此节点的值应该比max的值小
if (max != null && root.val >= max.val) return false;
//判断左子树合法性:max的值为此节点的值,左子树上每个节点都要小于此节点的值
//判断右子树合法性:min的值为此节点的值,右子树上每个节点都要大于此节点的值
return isValidBST(root.left, min, root) && isValidBST(root.right, root, max);
}
(3)二叉搜索树特性:中序遍历序列为递增序列
根据这个特性,我们可以分析得到的中序遍历序列:
假设有一个递增序列 a=[1,2,3,4,5,6,7]。
如果我们交换两个不相邻的数字,例如 2 和 6,原序列变成了 a=[1,6,3,4,5,2,7],那么显然序列中有两个位置不满足 a i < a i + 1 a_i
如果我们交换两个相邻的数字,例如 2和 3,此时交换后的序列只有一个位置不满足 a i < a i + 1 a_i
因此整个值序列中不满足条件的位置或者有两个,或者有一个。
2.题目
二叉搜索树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
示例 1:
输入: [1,3,null,null,2]
1
/
3
\
2
输出: [3,1,null,null,2]
3
/
1
\
2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/recover-binary-search-tree
3.代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void inorder(TreeNode* root,vector<int> &nums){
if(root==nullptr)return;
inorder(root->left,nums);
nums.push_back(root->val);
inorder(root->right,nums);
}
//找到需要交换的两个val
pair<int,int> findSwapPair(vector<int> &nums){
int x=-1,y=-1;
//此序列是递增序列
//如果只有一处 i>j,i和j就是
//如果有两处 i>j,i和j就是第一处的第一个数和第二处的第二个数
for(int i=0;i<nums.size()-1;i++){
if(nums[i]>nums[i+1]){
y=nums[i+1];//如果有第二处,此时值也被覆盖了
if(x==-1){//第一处
x=nums[i];
}else{
break;
}
}
}
return {x,y};
}
//交换x和y代表的节点
//x=1,y=3
void recover(TreeNode* root,int count,int x,int y){
if(root==nullptr)return;
if(root->val==x||root->val==y){
if(root->val==x)root->val=y;
else root->val=x;
count--;
if(count==0)return;
}
recover(root->left,count,x,y);
recover(root->right,count,x,y);
}
void recoverTree(TreeNode* root) {
vector<int> nums;
inorder(root,nums);
pair<int,int> swapped=findSwapPair(nums);
recover(root,2,swapped.first,swapped.second);
}
};
4.语法知识补充
(1)函数的引用参数:
在定义函数形参的时候加上引用符号&即可,传递实参的时候不需要再加。
(2)数据结构pair用法:
//【定义】
pair<int,int> swapped;
//【作为函数返回值】
pair<int,int> findSwapPair(vector<int> &nums){
return {x,y};
}
//【访问】
swapped.first;
swapped.second;
(3)控制递归的次数:
可以使用一个count变量,作为递归函数的参数,每次减一,到0时就return。
//【定义递归函数】
void recover(TreeNode* root,int count,int x,int y){
if(root==nullptr)return;
if(root->val==x||root->val==y){
count--;
if(count==0)return;
}
recover(root->left,count,x,y);
recover(root->right,count,x,y);
}
//【调用递归函数,传入count】
recover(root,2,swapped.first,swapped.second);