使用Sklearn模块建立聚类、回归、分类模型并评价

数据预处理和降维

首先来学习下加载数据集、划分数据集、数据预处理以及PCA降维

# 加载数据集
from sklearn.datasets import load_boston

boston = load_boston()
boston_data = boston['data']
boston_target = boston['target']
boston_names = boston['feature_names']
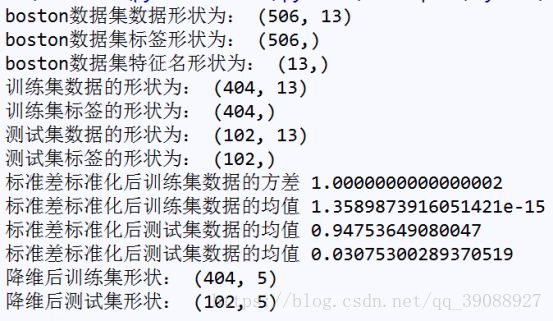
print('boston数据集数据形状为：', boston_data.shape)
print('boston数据集标签形状为：', boston_target.shape)
print('boston数据集特征名形状为：', boston_names.shape)

# 划分数据集
from sklearn.model_selection import train_test_split
import numpy as np

boston_data_train, boston_data_test, \
boston_target_train, boston_target_test = \
    train_test_split(boston_data, boston_target,
                     test_size=0.2, random_state=42)
print('训练集数据的形状为：', boston_data_train.shape)
print('训练集标签的形状为：', boston_target_train.shape)
print('测试集数据的形状为：', boston_data_test.shape)
print('测试集标签的形状为：', boston_target_test.shape)

# 使用sklearn的转换器进行数据预处理
from sklearn.preprocessing import StandardScaler

stdScaler = StandardScaler().fit(boston_data_train)
boston_trainScaler = stdScaler.transform(boston_data_train)
boston_testScaler = stdScaler.transform(boston_data_test)
print('标准差标准化后训练集数据的方差', np.var(boston_trainScaler))
print('标准差标准化后训练集数据的均值', np.mean(boston_trainScaler))
print('标准差标准化后测试集数据的均值', np.var(boston_testScaler))
print('标准差标准化后测试集数据的均值', np.mean(boston_testScaler))

# 使用转换器进行PCA降维
from sklearn.decomposition import PCA

pca = PCA(n_components=5).fit(boston_trainScaler)
boston_trainPca=pca.transform(boston_trainScaler)
boston_testPca=pca.transform(boston_testScaler)
print('降维后训练集形状：',boston_trainPca.shape)
print('降维后测试集形状：',boston_testPca.shape)

运行结果如图

聚类模型的构建与评价

聚类算法中我们以kmeans为例对种子数据进行分析，并创建模型并评价

import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans

seeds = pd.read_csv('f:/data/seeds_dataset.txt', sep='\t')
# 处理数据
seeds_data = seeds.iloc[:, :7].values
seeds_target = seeds.iloc[:, 7].values
seeds_names = seeds.columns[:7]
stdScale = StandardScaler().fit(seeds_data)
seeds_dataScale = stdScale.transform(seeds_data)

# 构建并训练模型
kmeans = KMeans(n_clusters=3, random_state=42).fit(seeds_data)
print('构建的kmeans模型为：', kmeans)

# 评价模型
from sklearn.metrics import calinski_harabaz_score

for i in range(2, 7):
    kmeans = KMeans(n_clusters=i, random_state=123).fit(seeds_data)
    score = calinski_harabaz_score(seeds_data, kmeans.labels_)
    print('seeds数据聚%d类calinski_harabaz指数为：%f' % (i, score))

结果如图

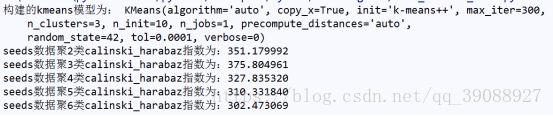
运行结果显示，在聚类数目为3时，calinski_harabaz指数最大，聚类效果最好

分类模型的构建与评价(对鲍鱼年龄特征进行预测)

分类模型中我们以SVM为例对鲍鱼年龄特征进行分析

import pandas as pd
from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

abalone = pd.read_csv('f:/data/abalone.data', sep=',')
abalone_data = abalone.iloc[:, :8]
abalone_target = abalone.iloc[:, 8]

# 连续型特征离散化
sex = pd.get_dummies(abalone_data['sex'])
abalone_data = pd.concat([abalone_data, sex], axis=1)
abalone_data.drop('sex', axis=1, inplace=True)

# 划分训练集、测试集
abalone_data_train, abalone_data_test, \
abalone_target_train, abalone_target_test = \
    train_test_split(abalone_data, abalone_target,
                     train_size=0.2, random_state=42)

# 标准化
abaloneScaler = StandardScaler().fit(abalone_data_train)
abalone_data_train_std = abaloneScaler.transform(abalone_data_train)
abalone_data_test_std = abaloneScaler.transform(abalone_data_test)

# 降维
pca = PCA(n_components=6).fit(abalone_data_train_std)
abalone_data_train_pca = pca.transform(abalone_data_train_std)
abalone_data_test_pca = pca.transform(abalone_data_test_std)

# 建模
svm_abalone = SVC().fit(abalone_data_train_pca, abalone_target_train)

# 评价
abalone_target_pre = svm_abalone.predict(abalone_data_test_pca)
print('svm的分类报告为：\n',
      classification_report(abalone_target_test, abalone_target_pre))

结果如图

结果表明对9的预测效果较好，其他较为欠缺

构建线性回归模型并评价

线性回归模型中我们以梯度提升回归树模型为例对房价数据进行分析建模并评价

import pandas as pd
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split

house = pd.read_csv('f:/data/cal_housing.data', sep=',')
house_data = house.iloc[:, :-1]
house_target = house.iloc[:, -1]
house_train,house_test,\
house_target_train,house_target_test=\
    train_test_split(house_data,house_target,
                     test_size=0.2,random_state=42)
GBR_house=GradientBoostingRegressor().fit(house_train,house_target_train)
print(GBR_house)

#评价
house_target_pre=GBR_house.predict(house_test)
from sklearn.metrics import explained_variance_score,\
    mean_absolute_error,mean_squared_error,\
    median_absolute_error,r2_score
print('梯度提升回归树模型的平均绝对误差为：',mean_absolute_error(house_target_test,house_target_pre))
print('梯度提升回归树模型的均方误差为：',mean_squared_error(house_target_test,house_target_pre))
print('梯度提升回归树模型的中值绝对误差为：',median_absolute_error(house_target_test,house_target_pre))
print('梯度提升回归树模型的可解释方差值为：',explained_variance_score(house_target_test,house_target_pre))
print('梯度提升回归树模型的R^2值为：',r2_score(house_target_test,house_target_pre))

结果如下

结果表明本次构建的梯度提升回归树模型的平均绝对误差和均方误差相对合理，且可解释方差值和R^2值较接近1，故本次构建的模型是一个较为有效的模型。