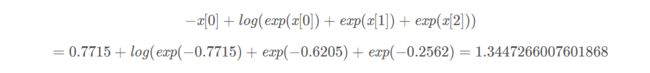pytorch学习笔记三：torch.nn下常见的几个损失函数详解

       在盘点常见损失函数之前，有必要先说一下在很多的损失函数中都出现的三个参数，也即size_average,reduce以及reduction，并且它们三个之间还存在一定的关系。

• size_average：bool类型；默认情况下，如果只有一个batch，每个batch有多个元素，那么误差计算结果是这个batch中多个元素的平均值；如果是有多个batch，然后每个batch有多个元素，那么误差计算的结果是将每个batch的平均值放到一块再求多个batch的平均值；如果把这个参数设置为False,那么只需要将计算平均值换成计算和即可，其他完全一样；默认该参数值为True；但是如果 reduce参数被指定为False，那么这个参数将被忽略，也即不起作用。

• reduce：bool类型；默认情况下，计算结果的形式会由size_average来决定，要么是求平均值，要么是求和，也即返回的是标量；但是如果 reduce参数被设置成False，那么既不求平均，也不求和，而是把每个batch，batch的每个元素的计算结果直接列出来，也即返回的是个向量，这个向量的形状和batch的个数以及每个batch里元素的个数是有关系的。默认该值是True。

• reduction：可以有三种取值，"none","mean","sum"，默认值是"mean"。如果你理解了对前面两个参数的解释，那么这里就很容易理解。如果是"none"，则既求平均，也不求和，返回的是向量；如果是"mean"，则计算的是平均值；如果是"sum"，则计算的是和；并且后两者返回的是标量。这里所说的求平均和求和与上面两个参数中所说的一模一样。

       下面以L1Loss损失函数(计算误差绝对值)来举例，来实际感受下上面三个参数的意义，重要的不是三者之间的关系，而是看一下上面提到的返回向量，求平均以及求和的具体结果是什么样的。所以，我们只需设置reduction这个参数即可以观察到三种计算结果。

import torch
from torch import nn

loss = nn.L1Loss(reduction="none")
input = torch.tensor(([1.,2.,3.],[4.,5.,6.]))
target = torch.tensor(([3.,2.,1.],[8.,5.,2.]))
output = loss(input, target)
print(output)

'''
输出：tensor([[2., 0., 2.],
              [4., 0., 4.]])
'''

import torch
from torch import nn

loss = nn.L1Loss(reduction="mean")
input = torch.tensor(([1.,2.,3.],[4.,5.,6.]))
target = torch.tensor(([3.,2.,1.],[8.,5.,2.]))
output = loss(input, target)
print(output)

'''
输出：tensor(2.)
'''

import torch
from torch import nn

loss = nn.L1Loss(reduction="sum")
input = torch.tensor(([1.,2.,3.],[4.,5.,6.]))
target = torch.tensor(([3.,2.,1.],[8.,5.,2.]))
output = loss(input, target)
print(output)

'''
输出：tensor(12.)
'''

好了，理解了上面三个参数的含义之后，开始盘点几个常见的损失函数。它们的参数里也会出现这几个参数，到时候就不再解释了。

torch.nn下的损失函数，准确来说它们不是函数，而是类，我们需要先实例化对象然后再使用。如下所示：

#实例化对象的时候可以指定参数
criterion = LossCriterion() 
loss = criterion(input, target) 

一、L1范数损失 L1Loss

• 计算的是input, target两者之差的绝对值,两者要具有相同的形状。input的形状是(N, * ),target的形状是(N, * ),如果reduction="none",那么输出的形状是(N, *)；这里的" * "指的是额外的任意维度。

torch.nn.L1Loss(size_average=None, 
                reduce=None, 
                reduction='mean')

二、均方误差损失 MSELoss

• 计算的是input, target两者的均方差,两者要具有相同的形状。input的形状是(N, *),target的形状是(N, *),如果reduction="none",那么输出的形状是(N, *)；这里的" * "指的是额外的任意维度。

torch.nn.MSELoss(size_average=None, 
                 reduce=None, 
                 reduction='mean')

三、交叉熵损失 MSELoss

• input的形状是(N,C),target的形状是(N,),如果reduction="none",那么输出的形状是(N,)

'''
weight:给每一个类别设置的权重，是一个一维向量，长度是C(C就是类别数)
ignore_index：一个int型整数，它作为索引值来指定target中的哪些值不需
要参与计算，也不用于梯度更新；当计算误差平均值的时候，只计算那些没有被
忽略的值
'''
torch.nn.CrossEntropyLoss(weight=None, 
                          size_average=None, 
                          ignore_index=-100, 
                          reduce=None, 
                          reduction='mean')

当训练有 C 个类别的分类问题时很有效. 可选参数 weight必须是一个1维 Tensor, 权重将被分配给各个类别. 对于不平衡的训练集非常有效。在多分类任务中，经常采用 softmax激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要 softmax激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算 loss。

假设我们的类别数为3，批量大小为2，那么input的形状是(2,3)，具体值设为torch.Tensor([[-0.7715, -0.6205,-0.2562],[-0.7715, -0.6205,-0.2562]])。标签值为target = torch.tensor([0,1]):

import torch
from torch import nn

entroy=nn.CrossEntropyLoss(reduction="none")
input=torch.Tensor([[-0.7715, -0.6205,-0.2562],
                    [-0.7715, -0.6205,-0.2562]])
target = torch.tensor([0,1])
output = entroy(input, target)
print(output)

'''
tensor([1.3447, 1.1937])
'''

我们来验证一下计算结果，这里以第一部分为例：

四、二进制交叉熵损失 BCELoss

• input的形状是(N, *),target的形状是(N, *),如果reduction="none",那么输出的形状是(N, *)；这里的" * "指的是额外的任意维度。

'''
weight:为每一个batch设置的权重，是一个长度等于batch的个数一维向量
'''
torch.nn.BCELoss(weight=None, 
                 size_average=None, 
                 reduce=None, 
                 reduction='mean')

import torch
from torch import nn

entroy=nn.BCELoss(reduction="mean")
input=torch.Tensor([[0., 1., 0.],[1., 0., 1.]])
target = torch.tensor([[1., 0., 1.],[0., 1., 0.]])
output = entroy(input, target)
print(output)

'''
输出：tensor(27.6310)
'''

五、BCEWithLogitsLoss

• BCEWithLogitsLoss损失函数把 Sigmoid层集成到了 BCELoss 类中. 这样比用一个简单的 Sigmoid 层和 BCELoss 在数值上更稳定, 因为把这两个操作合并为一个层之后, 可以利用 log-sum-exp的技巧来实现数值稳定。
• input的形状是(N, *),target的形状是(N, *),如果reduction="none",那么输出的形状是(N, *)；这里的" * "指的是额外的任意维度。

'''
weight:为每一个batch设置的权重，是一个长度等于batch的个数一维向量
pos_weight：是为batch中的每个元素设置的权重，应用到所有batch，是一个
长度等于类别个数，也就是每个batch中的元素的个数的一维向量
'''
torch.nn.BCEWithLogitsLoss(weight=None, 
                           size_average=None, 
                           reduce=None, 
                           reduction='mean', 
                           pos_weight=None)

下面我们用一个例子来验证一下，看看BCEWithLogitsLoss的计算结果是不是和sigmoid+BCELoss的计算结果是一样的。

sigmoid+BCELoss

entroy=nn.BCELoss(reduction="mean")
input=torch.Tensor([[0.9, 1., 0.9],[0.1, 0., 0.1]])
input=nn.Sigmoid()(input)
target = torch.tensor([[1, 0., 1.],[0., 1., 0.]])
output = entroy(input, target)
print(output)

'''
输出：tensor(0.6963)
'''

BCEWithLogitsLoss

entroy=nn.BCEWithLogitsLoss(reduction="mean")
input=torch.Tensor([[0.9, 1., 0.9],[0.1, 0., 0.1]])
target = torch.tensor([[1, 0., 1.],[0., 1., 0.]])
output = entroy(input, target)
print(output)

'''
输出：tensor(0.6963)
'''

可以看到，两者的计算结果是一样的。