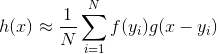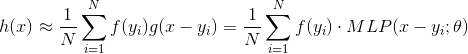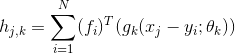小白科研笔记：深度连续卷积和它在深度补全中应用

1. 前言

由于LiDAR点云稀疏的特性，根据它得到的LiDAR深度图也是稀疏的。然而相机采集到的信息却是稠密的。这样一种反差对LiDAR-Camera多传感器信息融合造成挑战。Continuous Convolution是近年处理LiDAR-Camera信息融合的方法之一。这篇博客尝试探究Continuous Convolution在深度补全的应用。我将主要参考下面两篇文章：

（1）Shenlong Wang, Simon Suo, Wei-Chiu Ma, Andrei Pokrovsky, and Raquel Urtasun. Deep parametric continuous convolutional neural networks. In CVPR, 2018；
（2）Yun Chen, Bin Yang, Ming Liang, and Raquel Urtasun. Learning joint 2d-3d representations for depth completion. In ICCV 2019；

注：有趣的是这些文章都是Uber Advanced Technologies Group和University of Toronto合作成果。Continuous Convolution的发源地也在这里。

2. 深度连续卷积网络

第二章的讨论是循序渐进的。先从理论层面讲解参数化连续卷积，以及参数化连续卷积层，和它的计算细节；再从应用角度讲解参数化连续卷积层的搭建，以及深度连续卷积网络的实现。这归功于文献（1）的行文严谨。

2.1 参数化连续卷积

为了讨论起见，我把Parametric Continuous Convolutions直译为参数化连续卷积。先介绍连续卷积（Continuous Convolutions）。设连续信号是（即输入特征图），核函数是，那么核函数卷积在连续信号上将得到连续卷积结果（即输出特征图）。该过程如下所示：

作者认为获取连续信号非常困难，因为实际应用中的物理模型非常复杂，并且观测者只能观察到曲线上数个采样点。因此实际计算中，不能按照上式计算理想的，但是可以根据观测到的采样点按照下面的公式近似计算：

机器学习通过让接近于预设值的方式（即训练过程），来学习核函数的构造。考虑到实际应用的复杂性，核函数也可能是极其复杂的。为了便于学习和训练，依据万能近似定理（Universal approximation theorem），可以把核函数近似看作是多层感知机（multi-layer perceptron，简称MLP）的输出。因此可以写成下面所示。是感知机的超参数，需要训练。

最终就能得到参数化连续卷积（参数化这个词就起源于超参数）：

2.2 参数化连续卷积层

参数化连续卷积层是Parametric Continuous Convolution Layer的直译，它是参数化连续卷积概念的延伸（概念摘出，hhh）。原文这里有些抽象，不便于说明。为了方便讨论，就举个跟深度补全（depth completion）相关的栗子（我这个例子中使用的符号跟原论文是有出入的）。设想一个的深度图，里面有一部分像素是有深度值的，另一部分像素是没有深度值的。这就是个残缺的深度图。深度补全就希望把那些没有深度值的像素补上深度值。可以说深度补全也是矩阵补全（matrix completion）的特殊情况。设那些有深度值的像素集合记为。假设咱提取了集合S的特征，这些特征集合记为，这些特征都是的向量。现在咱想利用已知信息S和F来补全一个像素的深度值，这个像素标记为。从参数化连续卷积考虑，的计算方式如下所示：

其中是MLP层，输出的向量。可以看作是已知特征向量的加权和，只不过权值函数由MLP表示，其参数需要学习训练。此外，的计算可以用一个稠密图表示。这是参数化卷积跟图卷积有着密切联系的原因。

跳出这个例子，给出参数化连续卷积层的一般表示。作为概念上的Layer，它的输入是已知元素集合，该集合对应的特征向量集合和目标元素，输出是一个的隐含层特征向量。输出是K维的，那么它的核函数也有K个。因此参数化连续卷积层可以写成：

具有几何意义。相当于在建立了一个局部坐标系，把集合的坐标转换到该局部坐标系下。在诸多点云算法中，这种局部坐标系是常用的工具，它能建立目标点和周围点的拓扑联系。

说点题外话。从上式可以发现：的计算离不开和它对应的。这种计算形式跟K近邻算法以及支撑向量机（Support Vector Machine，简称SVM）是非常相似的。在SVM中，一个区域预测值的计算时根据Support Vectors对应特征加权和得到的。所以集合S也带有Support的味道。因此在原文中，集合S叫做support domain，译为支撑区域。此外这种“近邻计算”方式跟PointNet也有相似的地方。PointNet的support domain可以看做它均匀采样后的点。总而言之，这种直观的几何式的思想在2017年之后就影响着稀疏点云深度学习的方向。英雄所见略同啊。

2.3 计算细节

计算量是，计算开销过大，并且实际应用中两个距离相隔很远的像素点之间的关联很小。为了节省计算开销，的计算只需要使用目标像素附近的那些支撑像素点和对应特征就行了。寻找附近的支撑像素点有两个办法：（1）KNN；（2）以画半径为r的圆。考虑到点云的无序性，KNN的实现需要借助于KD树加速。

注：KD树在CPU上运行很简单，但是处理上万个点云，速度达不到实时要求。KD树在GPU上运行需要Flann的CudaAPI，但是Flann库不太好和python合起来。pyflann貌似不支持GPU下调用。基于Pytorch实现的PointNet++提供了一些近邻搜索的功能函数，也许可以试试吧。

2.4 特殊情况

在一些特殊情况下，参数化连续卷积会向一些常见情形转化。如果集合是完全稠密的（e.g. 没有空洞的深度图），那么参数化连续卷积就会变成普通卷积。如果核函数是Guassian形式的核函数，那么参数化连续卷积就是一个滤波算法（Filter）或者变成一个条件随机场（CRF）。如果仅仅包括目标元素周围的区域，那么参数化连续卷积对应为一阶空域图卷积（First-order spatial graph convolution）。

注：在论文中，参数化连续卷积的实现依赖于KNN，其实它性质上就等同于一阶空域图卷积了。关于图卷积的知识，后续有空也会做探究。

2.5 参数化连续卷积层的搭建

一个参数化连续卷积层的搭建如下图所示。输入是点云的xyz坐标和它的特征。输出是点云卷积后的特征（维度为O）。

                                                                    图1：参数化连续卷积层的示意图

在这个示意图中，使用KNN方法获取目标点周围的邻近点，作为支撑点（Supporting Points）。图1明确指出需要用KD树来实现KNN。Supporting Points Indices是一个N*K的张量。N是输入点的数量。K指的是某一点周围最近的K个点的索引（Indices）。Suppor Point Coordinates是一个N*K*3的张量，表示某一点周围最近的K个点的相对坐标，即。Support Point Feature是一个N*K*I的张量I，表示某一点周围最近的K个点的输入特征，对应。把Support Point Coordinates输入到两层全连接（FC）层，得到Support Point Weights，它是一个N*K*I*O的张量，对应。Weighted Sum就是的计算过程。最后得到输出点云特征，它是N*O的张量。理解的话，倒并不难编程。

2.6 深度连续卷积网络的搭建

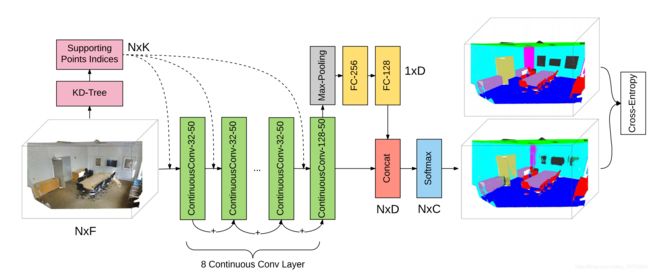
在2.5节讨论了参数化连续卷积层的搭建，这里将进一步研究深度连续卷积网络（Deep Parametric Continuous CNNs）的搭建。作者给出的点云语义分割示例网络如下图所示：

                                                                     图2：深度连续卷积网络示意图

Supporting Points Indices的概念在图1已经说明了。支撑点集是连续卷积必要输入之一。支撑点集就是目标点的近邻点，通过KD树调用KNN的方式实现。ContConv-x-y就是连续卷积层。xy分别表示其内两层FC层的神经元个数，这个在图1有体现。因此ContConv-x-y输出是N*y的张量。Concat处对应的残差连接（Residue connections）。PointNet系列也有池化和残差连接的网络方式。网络也会考虑batch normalization。语义分割旨在确定每一点的分类，多分类问题需要用到softmax。分类问题常用的损失函数就是交叉熵（Cross-Entropy）。

2.7 总结

稀疏点云是无序并且稀疏的。从稀疏点云上学习特征，会考虑到目标点的特征和它周围点特征的关联。具体实现的办法会有很多。其中，参数化连续卷积和PointNet系列就是近几年较为成功的方法之一。

3. 连续卷积在深度补全上的应用

主要讨论文献（2）。这篇文献的核心创新点有两个：（1）提出2D-3D fuse block；（2）提出带2D-3D fuse block的深度补全网络。网络效果当时排KITTI深度补全榜首，现在排前五。现有的top深度补全网络大多都是细节复杂的，要么网络设计有很多技巧设计复杂损失函数训练过程，要么需要额外数据集等各种数据增强方法。这篇文章的简洁和直观的几何含义吸引了我（笑哭笑哭）。在这一章，我会按照创新点的顺序逐次讲解。

3.1 2D-3D融合模块

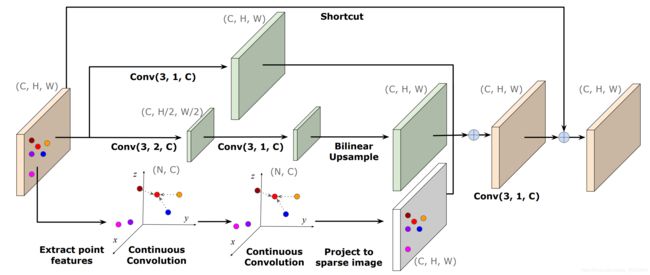
2D-3D融合模块是2D-3D fuse block的直译。该模块使用了连续卷积的概念。深度补全的概念在第2.2节的例子中讲解了，这里就不再重复。深度补全旨在利用稠密RGB信息去引导LiDAR深度图的补全。回到这篇论文，在2D-3D fuse block这个词中，2D指RGB特征，3D指的是点云特征（深度图反投影而成）。fuse值RGB特征和点云特征的融合。所以作者设计2D-3D融合模块是期望有效处理RGB-D信息。2D-3D融合模块如下图所示：

                                                                      图3：2D-3D fuse block示意图

2D-3D融合模块输入是一个张量为的2D输入特征图，以及一个张量为的点云。它的输出是同尺寸的的2D特征图。LiDAR-camera的外参数是已知量，这样可以把点云投影在成像平面上，进而通过缩放，确定点云在2D输入特征图上的位置。2D-3D融合模块由两个部分组成，分别是multi-scale 2D convolution network和3D continuous convolution network。

首先介绍多尺度2D卷积网络（multi-scale 2D convolution network）。作者把2D卷积标记为，其中k是核函数的尺寸，s是卷积stride参数，c是输出通道数。多尺度2D卷积网络由两个分支组成，分别是conv(3,1,C)分支和conv(3,2,C)分支。每次卷积之后使用Batch normalization和ReLU激活函数。原理比较简单。

其次介绍3D连续卷积网络（3D continuous convolution network）。考虑到雷达点云是稀疏的，对稀疏点云做卷积，就会需要参数化连续卷积。这已经在第二章做了详细讲解。具体实现过程是这样的：（0）前提条件，获取点云的KNN近邻点索引；（1）获取的点云的特征。把点云投影在2D输入特征图上，投影点的特征就是对应点云的特征。（2）的点云做连续卷积。对于目标点，它的连续卷积特征可以计算方式如下所示。（3）把点投在一张空白2D特征图上，投影点在空白2D特征图上的特征是连续卷积的结果。

其中是的近邻点。是点对应特征。MLP是两层全连接层，第一层包含C/2个神经元，而第二层包含C个神经元。W是一个C*C的权值矩阵。MLP的计算同样包含Batch normalization和ReLU激活函数。

最后把多尺度2D卷积网络和3D连续卷积网络的结果拼接起来得到，做些卷积处理，得到2D-3D fuse block的输出。

3.2 深度补全网络

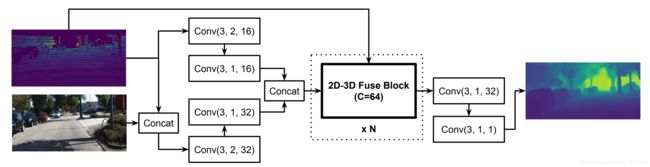
理解了2D-3D fuse block，再看深度补全网络就会非常简单。网络原理图如下图所示。 把2D-3D fuse bloc叠起来即可，因为它的输入输出的2D特征图尺寸一样。损失函数设计比较简单，这里就不讨论了。

                                                                                 图4：深度补全网络

3.3 总结

2D-3D fuse block思想很直观，结构有很好的扩展性。也许有更为广泛的用途。2D-3D fuse block核心是连续卷积，它在3d目标识别也能发挥巨大的作用，可以参考我的另外一篇博客。