二维差分数组和二维前缀和的个人看法

一维差分数组和前缀和都挺熟悉的，做题在打cf的时候做到了一个看别人用二维差分数组求前缀和的题，惊呆了，于是来补了下这方面的知识。

在学习和理解二维的时候，我们拿一维来对比就行了，思想是类似的但是略有所不同。

设一个二维数组a[i][j] 那么它的二维前缀和即为从(i,j) 到原点(0,0) 所有数之和，或者说这个矩形的大小。前缀和不是单用来求和的，而是在查询某一段区间的值时，能有O(1) 的高效。那么，怎么用前缀和求某个区间的值呢，画个图你就知道了。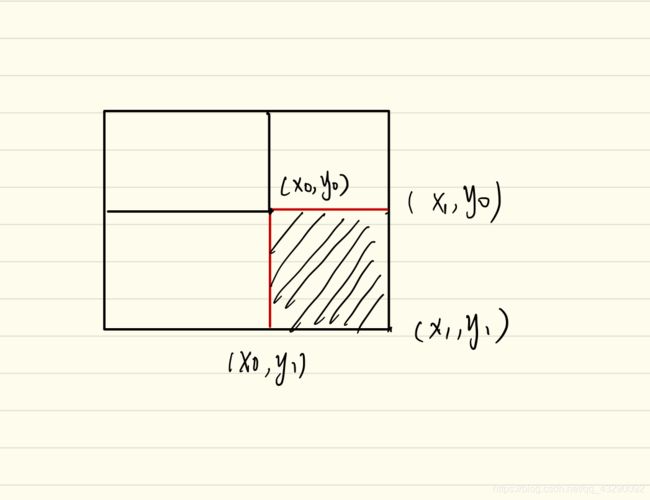
那么它的区间大小为ans=sum(x1,y1)-sum(x0,y1)-sum(x1,y0)+sum(x0,y0)

可是光求前缀和是不够的，当你需要对数组进行操作修改时，遍历每一个元素复杂度很高，这个时候可以维护一个差分数组，对比一维的差分数组，当对区间进行+x时，只需要在区间首位进行操作即可。

这里需要重点注意的是，浏览了不少关于差分数组的博客，都明确表示了，差分数组并不是真正的差分，不代表原数组中哪两个值的差分，只是用来记录原数组的变化，利用的是差分的思想，仔细想想确实如此。但是我个人认为，差分数组其实可以看成a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1] 的值，这样理解起来就会容易许多。
首先从一维差分数组的角度来说，差分就是与前一个做差，对比到二维，我们也与前一个做差，只不过重复了，所以我们再加上a[i-1][j-1]
其次，从数据上来看，差分数组的值确实也符合这一规律
而且，差分和求前缀和本身就是一个紧密联系的过程，对差分求前缀和和对前缀和做差分都是原数组，而且这一看法能很好的解释与理解对差分数组的操作。

	sum[a][b]++;      //a,b 为左上角坐标
    sum[a][y + 1]--;   // x,y 为右下角坐标
    sum[x + 1][b]--;
    sum[x + 1][y + 1]++;

最后，放上昨天的cf d题 是我看到某个红名大佬的代码花了不少时间理解的，我认为就是二维差分前缀和的思想，如果有不对的地方，还希望各位大佬指正。
Codeforces Round #578 (Div. 2) D White Lines

#include 
using namespace std;
 
char arr[2010][2010];
int sum[2010][2010];
 
void add(int a, int b, int x, int y)
{
 
    sum[a][b]++;
    sum[a][y + 1]--;
    sum[x + 1][b]--;
    sum[x + 1][y + 1]++;
}
 
int main()
{
    //freopen("in", "r", stdin);
    //freopen("out", "w", stdout);
 
    int n, k, i, j;
    scanf("%d%d", &n, &k);
    for(i = 1; i <= n; i++)
        scanf("%s", arr[i] + 1);
 
    for(i = 1; i <= n; i++)
    {
        int a = -1, b = -1;
        for(j = 1; j <= n; j++)
        {
            if(arr[i][j] == 'B')
            {
                if(a == -1)
                    a = j;
                b = j;
            }
        }
 
        if(a == -1)
            add(1, 1, n, n);
        else if(b - a + 1 <= k)
            add(max(1, i - k + 1), max(1, b - k + 1), i, a);
    }
 
    for(j = 1; j <= n; j++)
    {
        int a = -1, b = -1;
        for(i = 1; i <= n; i++)
        {
            if(arr[i][j] == 'B')
            {
                if(a == -1)
                    a = i;
                b = i;
            }
        }
 
        if(a == -1)
            add(1, 1, n, n);
        else if(b - a + 1 <= k)
            add(max(1, b - k + 1), max(1, j - k + 1), a, j);
    }
 
    int r = 0;
    for(i = 1; i <= n; i++)
    {
        for(j = 1; j <= n; j++)
        {
            sum[i][j] += sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1];
            r = max(r, sum[i][j]);
        }
    }
 
    printf("%d\n", r);
    return 0;
}

这里凭个人的理解稍作解释。先找到最上下左右的黑色，然后扫描每一行和列，第一个if判断为如果这一行全为白色，没有黑色，那么就对整个矩阵进行add操作。怎么理解这里的add操作呢，代码中的sum数组存的就是上文中的差分数组，是 若在当前位置(i,j)以k长度刷白，则能有多少行列为全白 的差分。 试想，若一行全为白色，则对整个数组中任意一个点进行操作，那么均可加1(这一行或者列）
第二个判断同理，以当前位置为右下角，那么左上角的矩阵中任意一点刷白都能覆盖到当前行或者列，所以都可以add