代码随想录算法训练day65---图论系列9《dijkstra(堆优化版)&Bellman_ford 算法》

代码随想录算法训练

—day64

---

前言

今天是算法营的第65天，希望自己能够坚持下来！
今天继续图论part！今日任务：
● dijkstra(堆优化版)
●Bellman_ford 算法

---

一、47. 参加科学大会-----dijkstra(堆优化版)

卡码网题目链接
文章讲解

朴素版的dijkstra因为用的是邻接矩阵（二维数组）来存储图，有n个节点就要开辟n*n的二维数组。

在最小生成树的时候，有两个算法，prim算法（从点的角度来求最小生成树）、Kruskal算法（从边的角度来求最小生成树）

那么当n很大的时候，也有另一个思考维度，即：从边的数量出发。

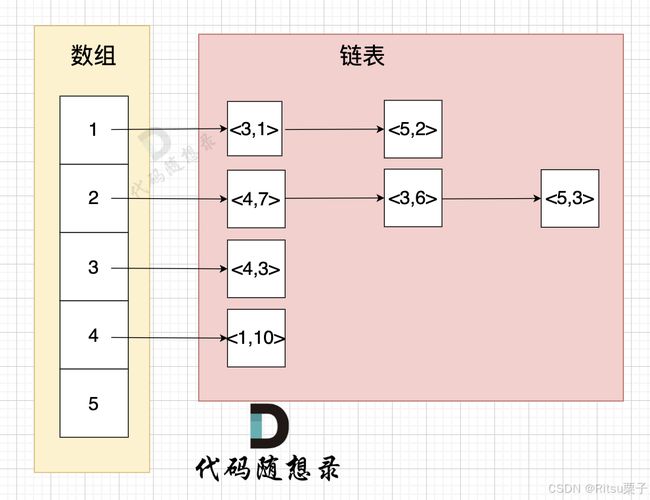
那么我们就考虑用邻接表来存储图，vector grid(n + 1);。但是因为题目是由权值的，所以这里我们用vector>> grid(n + 1);

但是在代码中 使用 pair 很容易让我们搞混了，第一个int 表示什么，第二个int表示什么，导致代码可读性很差，或者说别人看你的代码看不懂。

所以可以定义一个结构体

struct Edge {
    int to;  // 邻接顶点
    int val; // 边的权重

    Edge(int t, int w): to(t), val(w) {}  // 构造函数
};

优化思路：
1.用邻接表来代替邻接矩阵存储图
2.因为有权值，定义一个结构体作为邻接表的类型vector grid(n + 1);
3.定义一个小顶堆，用优先队列来排序所有边的权值，按小到大排序。
4.循环弹出优先队列中的边，接着依然是标记访问过的节点，并且更新minDist。

更新minDist：
朴素dijkstra是for循环遍历所有节点，然后更新当前节点cur指向的节点对应的minDist。那么使用邻接表存储图之后，就不需要遍历所有节点了，直接遍历cur节点的那一个表就是所有“cur指向的节点”了，所以

// 3. 第三步，更新非访问节点到源点的距离（即更新minDist数组）
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点，cur指向的节点为 edge
    // cur指向的节点edge.to，这条边的权值为 edge.val
    if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
        minDist[edge.to] = minDist[cur.first] + edge.val;
        pq.push(pair<int, int>(edge.to, minDist[edge.to]));
    }
}

这里需要注意更新完minDist后要把新的minDist作为边最新的权值添加到优先队列中。

代码如下：

#include
#include
#include
#include
#include
using namespace std;
 
//小顶堆
class mycomparison {
    public:
        bool operator()(const pair<int,int>& lhs, const pair<int,int>& rhs){
            return lhs.second > rhs.second;
        }
};
 
//定义一个结构体来表示带权值的边
struct Edge {
    int to; //边
    int val; //权值
     
    Edge(int t, int w):to(t),val(w){} //构造函数
};
 
int main() {
    int n, m, p1, p2, val;
    cin >> n >> m;
     
    vector<list<Edge>> grid(n + 1);
     
    for (int i = 0; i < m; i++) {
        cin >> p1 >> p2 >> val;
        //p1指向p2，权值为val
        grid[p1].push_back(Edge(p2, val));
    }
     
    int start = 1;
    int end = n;
     
    vector<bool> visited(n + 1, false);
    vector<int> minDist(n + 1, INT_MAX);
     
    //优先队列，存放pair<节点，源点到该节点的距离>，vector是指定优先队列的存放容器
    priority_queue<pair<int,int>, vector<pair<int,int>>, mycomparison> pq;
     
    //初始化队列，源点到源点的距离为0，所以初始化为0
    pq.push(pair<int,int>(start, 0));
     
    minDist[start] = 0; //起始点到自身的距离为0
     
    while (!pq.empty()) {
        //1.第一步，找到离源点最近的节点且该节点未被访问过（通过优先队列实现了）
        //<节点，源点到该节点的距离>
        pair<int, int> cur = pq.top(); pq.pop();
         
        if (visited[cur.first]) continue;
         
        //2.第二步，标记该节点被访问过
        visited[cur.first] = true;
         
        //3.第三步，更新minDist数组
        for (Edge edge: grid[cur.first]) { //遍历cur指向的节点，cur指向的节点为edge
            //cur指向的节点edge.to, 这条边的权值为edge.val
            if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) {
                minDist[edge.to] = minDist[cur.first] + edge.val;
                pq.push(pair<int,int>(edge.to, minDist[edge.to]));
            }
        }
    }
     
    if (minDist[end] == INT_MAX) cout << -1 << endl;
    else cout << minDist[end] << endl;
}

---

二、94. 城市间货物运输 I—Bellman_ford 算法

卡码网题目链接
文章讲解

本题依然是单源最短路问题，求 从 节点1 到节点n 的最小费用。 但本题不同之处在于 边的权值是有负数了。所以不能用dijkstra算法。

Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作（n为节点数量），从而求得目标最短路。

对所有边进行1次松弛操作，就是获得 与起点 一条边相连的节点最短距离。
对所有边进行2次松弛操作， 就是获得 与起点 两条边相连的节点的最短距离。
以此类推，最后进行n-1次松弛操作就会或的 起点与n-1条边相连的节点的最短距离。

代码如下：

#include
#include
#include
#include
using namespace std;
 
int main() {
    int n, m, p1, p2, val;
    cin >> n >> m;
     
    vector<vector<int>> grid;
     
    //将所有边保存起来
    for (int i = 0; i < m; i++) {
        cin >> p1 >> p2 >> val;
        grid.push_back({p1, p2, val});
    }
     
    int start = 1;
    int end = n;
     
    vector<int> minDist(n + 1, INT_MAX);
    minDist[start] = 0;
     
    //对所有边 松弛 n-1次
    for (int i = 1; i < n; i++) {
        for (vector<int> &side: grid) { //遍历每一条边，进行松弛
            int from = side[0];
            int to = side[1];
            int price = side[2];
             
            //松弛操作 minDist[from] != INT_MAX 防止从未计算过的节点出发
            if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
                minDist[to] = minDist[from] + price;
            }
        }
    }
     
    if (minDist[end] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[end] << endl;
}

---

总结

• dijkstra算法堆优化：
  1.用邻接表来代替邻接矩阵存储图
  2.因为有权值，定义一个结构体作为邻接表的类型vector grid(n + 1);
  3.定义一个小顶堆，用优先队列来排序所有边的权值，按小到大排序。
  4.循环弹出优先队列中的边，接着依然是标记访问过的节点，并且更新minDist。

• Bellman_ford 算法：
  1.适合权值有负数的求起点到终点的最短距离问题
  2.对所有边进行n-1次的松弛操作
  3.什么是松弛？

if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
    minDist[to] = minDist[from] + price;
}

明天继续加油！