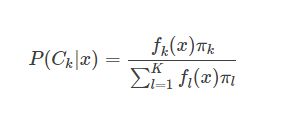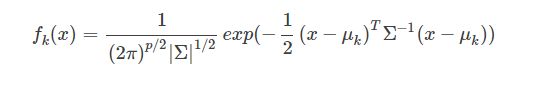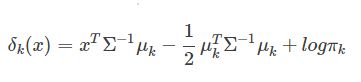人工智障学习笔记——机器学习(12)LDA降维

一.概念

LDA：Linear Discriminant Analysis (也有叫做Fisher Linear Discriminant)。与PCA一样，是一种线性降维算法。不同于PCA只会选择数据变化最大的方向，由于LDA是有监督的（分类标签），所以LDA会主要以类别为思考因素，使得投影后的样本尽可能可分。它通过在k维空间选择一个投影超平面，使得不同类别在该超平面上的投影之间的距离尽可能近，同时不同类别的投影之间的距离尽可能远。从而试图明确地模拟数据类之间的差异。

二.算法

在LDA中，我们假设每一个类别的数据服从高斯分布，且具有相同协方差矩阵Σ。 为了得到最优的分类器，我们需要知道类别的后验概率P(Ck|x)。根据贝叶斯定理：

其中，πk 是类别Ck的先验概率，是已知的，那么主要就是求出类条件概率密度函数fk(x)。不同的算法，对这个类条件概率密度函数的假设都不同。

例如：

线性判别分析（LDA）假设fk(x)是均值不同，方差相同的高斯分布
二次判别分析（QDA）假设fk(x)是均值不同，方差也不同的高斯分布
高斯混合模型（GMM）假设fk(x)是不同的高斯分布的组合
很多非参数方法假设fk(x)是参数的密度函数，比如直方图
朴素贝叶斯假设fk(x)是Ck边缘密度函数，即类别之间是独立同分布的

那么LDA的类条件概率密度函数可以写为

一个线性分类器，在判别式函数δk(x)或者后验概率函数P(Ck|x)上加上一个单调函数f(⋅)后，可以得变换后的函数是x的线性函数，而得到的线性函数就是决策面。LDA所采用的单调变换函数f(⋅)和前面提到的Logistics Regression采用的单调变换函数一样，都是logit 函数：log[p/(1−p)]，对于二分类问题有：

可以看出，其决策面是一个平面。根据上面的式子，也可以很容易得到LDA的决策函数是：

三.sklearn提供的API

sklearn的discriminant_analysis提供了LDA方法（LinearDiscriminantAnalysis）

def __init__(self, solver='svd', shrinkage=None, priors=None,
                 n_components=None, store_covariance=False, tol=1e-4):
        self.solver = solver
        self.shrinkage = shrinkage
        self.priors = priors
        self.n_components = n_components
        self.store_covariance = store_covariance  # used only in svd solver
        self.tol = tol  # used only in svd solver

solver : 即求LDA超平面特征矩阵使用的方法。可以选择的方法有奇异值分解"svd"，最小二乘"lsqr"和特征分解"eigen"。一般来说特征数非常多的时候推荐使用svd，而特征数不多的时候推荐使用eigen。主要注意的是，如果使用svd，则不能指定正则化参数shrinkage进行正则化。默认值是svd
shrinkage：正则化参数，可以增强LDA分类的泛化能力。如果仅仅只是为了降维，则一般可以忽略这个参数。默认是None，即不进行正则化。可以选择"auto",让算法自己决定是否正则化。当然我们也可以选择不同的[0,1]之间的值进行交叉验证调参。注意shrinkage只在solver为最小二乘"lsqr"和特征分解"eigen"时有效。
priors ：类别权重，可以在做分类模型时指定不同类别的权重，进而影响分类模型建立。降维时一般不需要关注这个参数。
n_components：即我们进行LDA降维时降到的维数。在降维时需要输入这个参数。注意只能为[1,类别数-1)范围之间的整数。如果我们不是用于降维，则这个值可以用默认的None。

实例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from mpl_toolkits.mplot3d import Axes3D

X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2,
                           n_clusters_per_class=1,class_sep =0.5, random_state =10)

fig = plt.figure('data')
ax = Axes3D(fig)
plt.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o',c=y)

print (y)
print (X)
fig = plt.figure('PCA')
pca = PCA(n_components=2)
pca.fit(X)
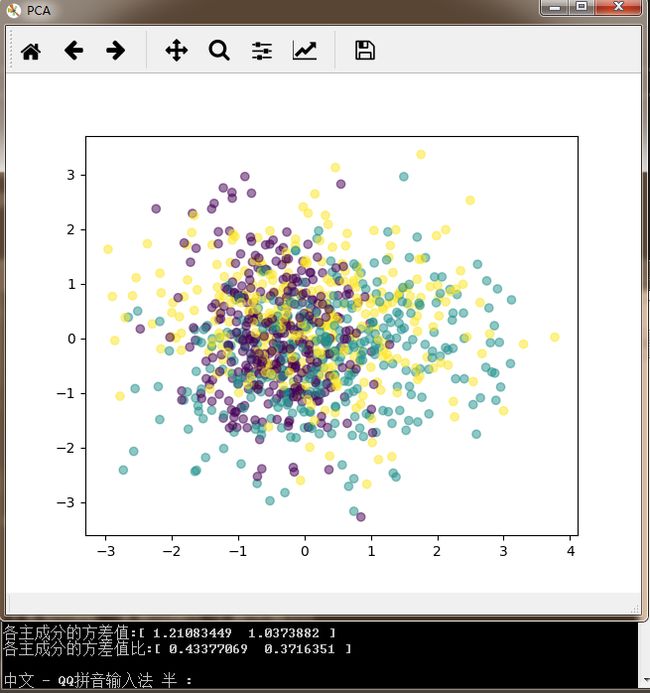
print("各主成分的方差值:"+str(pca.explained_variance_))
print("各主成分的方差值比:"+str(pca.explained_variance_ratio_))
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y,alpha=0.5)
fig = plt.figure('LDA')
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X,y)
X_new = lda.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o',c=y,alpha=0.5)

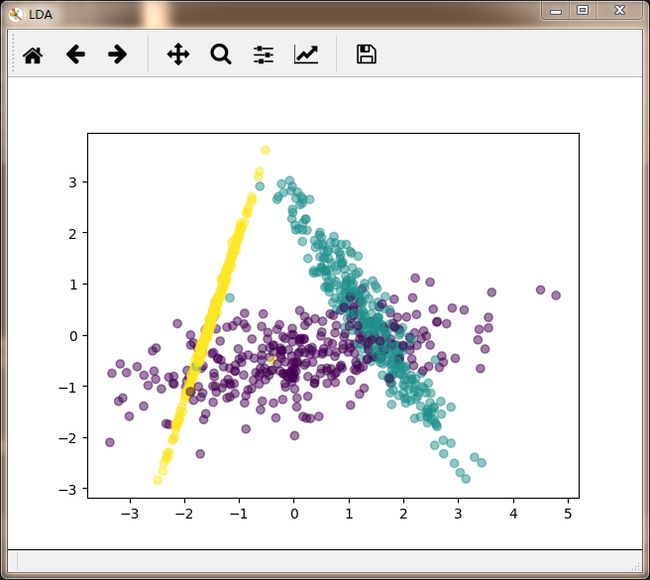
plt.show()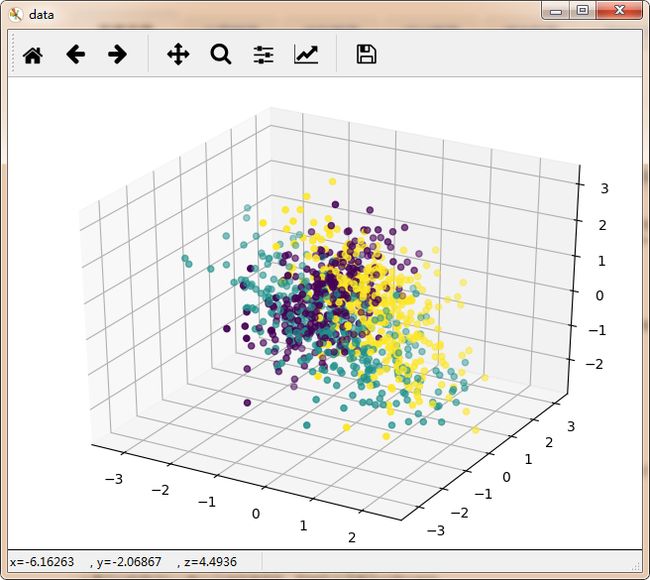

可以看到，没有利用类别信息的PCA降维后螺旋爆炸升天，样本特征和类别的信息关联几乎完全丢失，简直石乐志。而LDA样本特征和类别信息之间还是可以保留的。

四.总结

LDA与PCA的最大的不同点在于，LDA是有监督的算法，而PCA是无监督的，因为PCA算法没有考虑数据的标签(类别)，只是把原数据映射到一些方差比较大的方向(基)上去而已。而LDA算法则考虑了数据的标签。所以一般来说，如果我们的数据是有类别标签的，那么优先选择LDA去尝试降维；当然也可以使用PCA做很小幅度的降维去消去噪声，然后再使用LDA降维。如果没有类别标签，那么肯定PCA是最先考虑的一个选择了。

五.相关学习资源

https://www.cnblogs.com/pinard/p/6249328.html

http://blog.csdn.net/daunxx/article/details/51881956

https://en.wikipedia.org/wiki/Linear_discriminant_analysis