自组织一致性哈希算法
自组织一致性哈希算法
1、一致性哈希算法及其用途
假设现在有一批数据需要均匀地分布在若干台服务器上,这批数据满足以下假定:
- 所有数据的访问频率一致。
- 数据的访问都是随机的。
- 不管数据规模多大,都希望数据的分布是均匀的
- 不断有新数据需要进入
- 不考虑单点失效的问题
假设1表明,程序访问每个数据的概率均等P(A) = P(B)。
假设2表明,数据与数据之间没有必然的依赖关系。也就是访问了A数据之后,再访问B数据的概率,与访问除B之外的任一数据的概率相等。也就是P(A|B) = P(A|C)。
假设4可以通过高可用方案来解决。
普通的哈希算法(如取模),透过主键取哈希值,可以使这些数据均匀分布在多个服务器中。但当服务器结点数目发生改变时,无法避免数据的迁移。
下面的定理说明了取模运算所导致的数据变动
定理1:n是正整数,a≠b,b>a>0, 若n≡r1(mod a) ,n≡r1(mod b),r1是n模a,b的最小正剩余,那么
- 若a与b互素,则n = r1 + a * b * t, t ∈Z+
- 若(a,b)=c,则n = r1 + (a * b / c) * t
证明:由同余式可导出不定方程 a * x - b * y = 0。
1)若a与b互素,则必定有x = b + b * t, y = a + a * t
由n = a * x + r1,代入即得 n = r1 + a * b * t’,t’= t + 1。
2)若(a,b)=c,不定方程两边除c得 a’* x – b’* y = 0 ,a’= a / c,b’=b / c。
方程有解x = b’ + b’ * t, y = a’ + a’ * t
把x代入n = a * x + r1,即得结论。
从上面的定理可以清楚看到,当模数发生变化时,余数不会发生变化最好的情况是b=2a,这时,大概只有1/2的数据不需要进行移动。
于是,出现了一致性哈希算法。一致性哈希算法可保证只有相对少量数据需要移动。其原理简单来说,就是把哈希值取值范围划分成若干个均等的区间。每台服务器负责存储某一个区间的值。
举例说明,假设有一批数据的哈希值被均分到0-q的值域,哈希函数可以继续沿用取模函数,假设key≡r1(mod q),若初始时集群中有n台机,每台机负责区域[t * q / n, ((t + 1) * q / n) - 1],若 t * q / n <= r1 < (t + 1) * q / n时,第t台机器就被命中。
假设现在要增加一台机,则只需要在现有的某个划分好的区域内,再分出两个子区间。例如把 [t * q / n, ((t + 1) * q / n) - 1]再划出[t * q / n, t * q / 2 - 1], [t * q / 2n , t * q / n - 1],这样只有第t台机需要把自身的1/2数据复制到新加入的节点中。这样,对整个数据集来说,实际上只有 1 / 2 * t的数据需要迁移,比定理1的最好情况还要少 1 / t 。
一致性哈希算法广泛应用于Memcached, redis等高速缓存组件中。
2、一致性哈希算法的问题
一致性哈希算法会造成“数据倾斜”。如上面的例子中,相对于其它n台机器,第t台机器和新加入的n+1 台机器,只承担了其它机器的 1 / 2 的负担。就算以后不断有新的数据加入,从命中概率而言,其数据量的数学期望也只有其它机器的1/2。
从目前已有的资料来看,还没有一个很好的办法来解决数据倾斜问题。
3、自组织一致性算法
下面介绍一个可以解决一致性哈希算法数据倾斜的办法。它是一种基于同余和历史记录的哈希算法,不仅所有数据不需要进行任何迁移,而且在假设5成立的前提下,可以准确算出当达到多大数据规模时,所有机器的负载将达到最终一致。
首先,前面知道当同余运算的模数发生变化时,余数也必定发生变化。如果以余数作为服务器号,当服务器数量发生改变时,那么数据必然发生迁移。所以需要为每条数据建立一个版本号,假设由1开始递增。当服务器数量发生变化后,记录当前服务器的数量,和每台服务器对应的余数。然后,将这些信息作为元数据写入分布式配置服务中心(例如zookeeper)中,并令当前的算法版本号+1。
做了上述记录后,服务器就可以添加(或减少)了。对于新加入的数据,就按新的服务器数量来进行取模求余,获得服务器号。对于已有的旧数据,就按配置中心记录的元数据,按旧有的规则来进行访问,这样,就可以在不迁移数据的情况下,兼容新旧两套不同的运算规则。
但与一致性哈希算法类似,这样的算法也会出现数据倾斜的问题,而且比原来的算法严重得多。这是因为没有做任何的数据迁移,新加入的机器一条数据都没有。
因此,希望新加入的结点主动承担更多的数据任务。(这也是为什么称之为自组织算法的原因)。这里引入虚拟结点的概念。虚拟结点,并不是真的物理结点,而只是相当于一种角色,一个身份的确认。假设原来有s台物理机,现在增加了Δs个节点,这Δs个节点中可能并不真的有Δs台物理机,其中可能只增加了一台物理机,但它却分担了Δs个物理机的角色。换过话说,它的负载增大了。为什么要增大它的负载,因为它刚加入,什么数据都没有,相对于来说,访问压力最轻。
在数据还在源源不断的地加入的前提下,不妨让这个结点承担更多的读写操作(主要还是写)。现在假设只增加一台物理机(实际应用中,特别是中小型项目,机器很多情况下都是一台台的加进去),那么在已有s台机器的情况(假设这s台机器的负载也是平均),Δs该如何选值,才能较快地使负载达到一致?
要讨论这个问题,必须要找一个参照物,比较好的参照物就是当前的数据规模n。从数据量的角度出发,我们希望在经过了n’个数据插入后,有以下等式:
N / s + n’ * Po = n’ * Pn
其中Po,Pn为新,旧服务器在新的规则下插入新数据的概率。令s’ = s + Δs,那么
Po = 1 / s +Δs , Pn =Δs / s + Δs。
代入原式并整理得
N’ = n * (s + Δs) / s * (Δs - 1) (1)
我们希望N’尽可能小,起码要比n小,那么会有
S + Δs – s * (Δs - 1) < 0
移项得: Δs > 2s / (s – 1)
也就是说当Δs > 2s / (s - 1), n’ 会比n 小。
因为Δs是一个整数,s – 1 与 s互素,所以不妨令Δs = (s - 1) * 2s / (s - 1) = 2s。
也就是说,令新加入的服务器承担2s个服务器的角色。那么整个集群就有3s个虚拟结点,除了新加入的服务器外,其余的服务器只承担了 1 / 3s的写任务。
而且把Δs = 2s,代入(1)式可得:n’ = (3 / (2s – 1)) * n。当s >1时,新加入的数据最多只需要3 / 4 的原来数据量,就可以使所有的机器保持负载一致。而且随着服务器的增加,所需要的新数据量呈线性下降。
当s=1时,为了更快地让两台服务器达到均衡,在两台服务器的数据量没有达到一致的情况下,可以让新加入的机器完全承担所有新数据的读写任务,只到两台机负载一致,才重新让两台一起负担。在这个转换的过程中,虚拟结点的概念就发挥作用,如前文所述,它只是一种身份的确认,所以虚拟结点是可以转移的。例如,在2#机还比较空闲的时候,2#机上有两个虚拟结点。等到负载一致了,2#通知配置中心,进行负载转移。因为n’是可以准确算出来的,所以2#机不去访问1#机,就知道何时应该触发身份转移。这个做法对于s > 1的情况也是适用的。
现在解决了在不进行数据迁移的情况下,如何让负载达到最终一致。但事实上,还有一个问题没有解决,就是负载一致后,新增加的虚拟结点如何均分。因为不可能让新加入的结点一直保持高负荷的状态,等它的数据量跟别人一样的时候,就要给它减负。
前面我们推导出Δs = 2s ,所以新的总结点数(含虚拟结点)总共是s’ = s + Δs = 3s,因为s 与s – 1是互素的,所以除非s=4,否则s- 1不整除s’。因此取Δs = 2s似乎不是好方案。可以继续尝试增大Δs,如令Δs= (s - 2) * s 。 其中Ф = Δs - 2s / (s – 1) = s^2 * (s - 3) / (s – 1) ,也就是当s >= 3时,Ф >= 0。而且从Ф的表达式可以知,当 s足够大时,Ф≈s^2。这样当s>=3时,总结点数就是s’= s + (s - 2) * s = s * (s - 1)。
显然可以被s-1整除,问题得到了解决。
S=1的时候,介绍过解决办法。剩下就只剩s=2时的情况,由于判别式Ф = 2s / (s – 1) = 4,所以Δs >= 4。又因为 3 | 2 + Δs,所以Δs = 1 + 3t,所以t 可取1或2,取2时有Δs = 7。
至此,所有的情况都讨论完毕。而且理论研究表明,不管s取何值,只要有充足的数据源,所有的服务器都将最终达到负载均衡的状态。
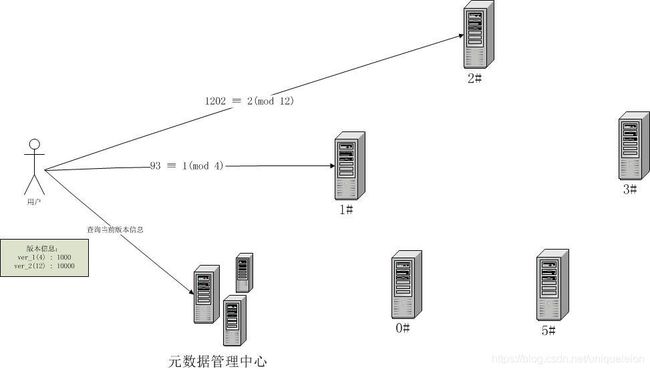
为了更好的描述算法,下面的图给出了算法运算过程。
现在已经解决了数据均匀分布的问题,下面的问题就是如何进行数据访问,如前文所述,数据缓存在服务器中,是有版本之分。怎么知道某个哈希值对应的是哪一个版本?
这时候元数据信息里面就需要有这样记录。对于数据是按序添加(如数据库中的自增主键)的情况,只需要记录当前版本号中当前的最大(或最小)的键值就够了。实际上绝大部分时候,缓存里面的数据缓存的就是数据库里获取到的数据。
每个版本号都对应着一个阀值,所有哈希值小于该阀值而大于上个版本的的阀值的数据都以这个版本的取模规则来进行访问。
下图给出了不同版本信息下,不同版本数据的访问情况:
对于无序数据,例如使用字符串摘要作为哈希,目前还未找到很高效的办法来进行处理。只能通过元数据中心去记录这些值与版本号之间的对应关系。但这势必造成元数据中心的访问压力和性能消耗。更理想的办法,是通过改造散列函数的办法,把版本号混合到哈希值中。例如令 n≡r1(mod s),n≡r2 (mod s’) , n + version * c ≡r3 (mod s) 和 n + version * c ≡r4(mod s’)从这两个同余式组中解出version的值(其中c是一个精心挑选的常数,例如是一个很大的质数)。这是因为这两组同余式组必定能导出一个形如 c * x + s * s’ * y = T的不定方程,解此不等方程即可以得版本号。若此方程无解,则缓存未击中。
4、两种一致性哈希算法比较
自组织一致性哈希算法(下简称自组织算法)比普通的一致性哈希算法(下简称原算法)有以下优点:
- 加入新结点不需要数据迁移
- 在新数量充足的情况下,不存在数据倾斜现象
但同时也有以下缺点:
- 算法较复杂,需要增加额外的配套服务(元数据管理)
- 在数据量不足的情况下,还是存在数据倾斜现象
缺点1相当于其优点而言,个人觉得可以忽略不计的。任何算法改进后,必定需要引入新的更复杂的机制。
缺点2在大数据环境下,几乎是不会出现。而且当需要增加服务器的时候,必然是到了现有服务器已经撑不住的体量了,所以数据量不足,导致负载不均这种情况,应该不会存在。
就算新增的数据量真达不到最终均衡的目标阀值时,其实也是可以通过在旧有服务器中淘汰掉一部分长时间不访问的冷数据,让这些冷数据落入新服务器中,从而达到最终一致。
至于怎么挑选冷数据,就需要用到一点数学上的知识。假设当前服务器的编号为k,在其之上的t1版本的数据中都有n≡k(mod s),假设新加入的机器承担了s+1#,s+2#........ s * (s - 1)#号机的虚拟结点角色。那么,要求哪些冷数据可以被分配到新服务器上,只需要求原来的同余式与n≡s+1(mod s * (s - 1)), n≡s+2(mod s * (s - 1)),……n≡s * (s - 1)-1(mod s * (s - 1))组成的s * (s - 1)个同余式组,再结合中国剩余定理就会得到s * (s - 1)个形如n = p + s * (s + q) * t的通式。再从这些通项式中找冷数据就容易得多。
5、算法延伸及应用
自组织一致性算法除了在快速缓存有广阔的应用场景外,在其它领域,例如在数据库领域,也会有广阔的应用场景。而且通过这种自组织的机制,服务器其实可以实现自己管理自己,而不需要人为干预。这也是自组织的一种重要体现。要是能实现自组织,配置运维人员就可以减少大量工作量。
目前,本人也正在研发一个应用自组织一致性算法来实现一个机制灵活简单,水平扩容的分布式关系型数据库DRDB(项目暂时命名为deadsea,原意为死海,引申为即便你对DRDB全无认知,也可以像操作普通RDB,一样操纵DRDB)
github地址:https://github.com/uniqueleon/DeadSea