2017 SEERC Divide and Conquer 树上差分

题目

题目大意：给出两颗树的复合图(即这张图是由两颗树拼起来的)，询问最小割掉多少条边，可以使得图不联通，并输出方案数。

分析

我觉得这是一道很难的题目，因为比较难想，前提结论比较多。

首先我们需要得到一个结论：就是割掉的边数不可能超过3。
证明：如果割掉的边数超过3，那么意味着每个点的度数都要 ≥4 ≥ 4 ，这也就是说，图中至少需要 2n 2 n 条边，而图是由两个树拼成的，边数只有 2n−2 2 n − 2 条边，显然不可能。

既然割掉的边数 2≤e≤3 2 ≤ e ≤ 3 ，那么我们可以得到结论：割掉的边既有属于A树的，也有属于B树的，如果割掉的边数为2，那么说明A树一条割边，B树一条割边。
如果割掉的边数为3，那么必有一棵树只包含一条割边。

因此，我们可以发现，如果我们以其中的一棵树(举例A树，这棵树只包含一条割边)作为主树的话，相当于将这颗树切成两边，并且求交叉于这棵树两边的B树树边的数量。
如图所示：

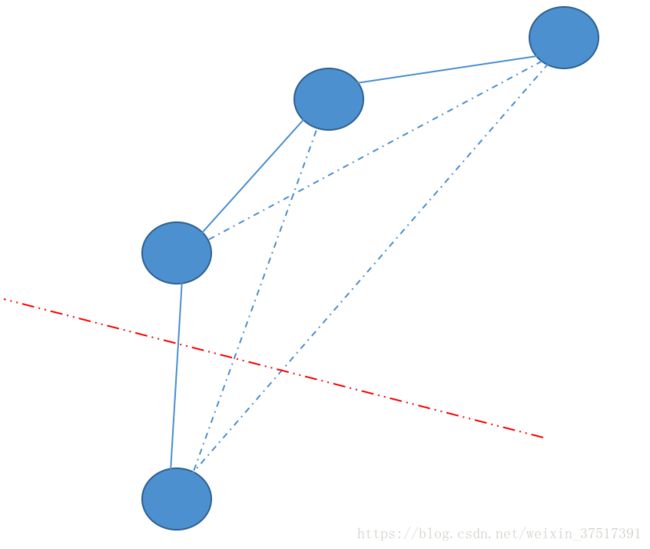
其中红线表示切割的位置，其中割掉的边数为 A A 树 1 1 条+ B B 树 2 2 条 = 3 3 条。

最后一个问题，怎么求A树的两个部分中B树横跨了多少边呢？
这就要用到树上差分了，由于A树的两个部分中必有一个是A树的子树，这意味着我们可以使用dfs来遍历，其次，B树的边如果链接的两个点是属于A树一个部分的时候，那么对结果没有影响。
因此，我们给B树的边 (u,v) ( u , v ) 做如下操作 mk[u]++,mk[v]++,mk[lca(u,v)]−=2; m k [ u ] + + , m k [ v ] + + , m k [ l c a ( u , v ) ] − = 2 ;
这样的话，我们只需要统计A的子树有 mk m k 的和，就可以知道链接A树的两个部分有多少条B树的边了。

注意

当答案是2的时候，我们直接输出方案数即可，而当答案是3的时候，我们需要交换A、B，并再次计算方案数，因为答案是3的情况方案数可能增加。

代码

#include 
#include 
#include 
using namespace std;
const int maxn = 1e5+7;
vector<int> A[maxn],B[maxn],V[maxn];
int n,dep[maxn],pa[maxn][22],mk[maxn];
inline int getint(){int tmp;cin>>tmp;return tmp;}
int mi = 1e9,ans = 0;
void dfs(int u,int fa){
    pa[u][0] = fa;
    dep[u] = dep[fa] + 1;
    for(auto v : V[u]){
        if(v == fa) continue;
        dfs(v,u);
    }
}
#define pr(x) cout<<#x<<":"<
int lca(int u,int v){
    if(dep[u] < dep[v]) swap(u,v);
    int d = dep[u] - dep[v];
    for(int i = 0;d;i++,d >>= 1) 
        if(d & 1) u = pa[u][i];
    for(int i = 20;~i;i--) 
        if(pa[u][i] != pa[v][i]) 
            u = pa[u][i],v = pa[v][i];
    if(u != v) u = pa[u][0],v = pa[v][0];
    return u;
}

void dfs2(int u,int fa){
    for(int v : V[u]){
        if(v == fa) continue;
        dfs2(v,u);
        mk[u] += mk[v];
    }
    if(u == 1) return ;
    if(mk[u] + 1 < mi){
        mi = mk[u] + 1;
        ans = 1;
    }
    else if(mk[u] + 1 == mi) 
        ++ans;
}

void solve(vector<int> A[maxn],vector<int> B[maxn]){
    for(int i = 1;i <= n;++i) V[i].clear();
    for(int u = 1;u <= n;++u) for(int v : A[u]){
        V[u].push_back(v);V[v].push_back(u);
    }
    memset(dep,0,sizeof(dep));
    memset(pa,0,sizeof(pa));
    memset(mk,0,sizeof(mk));
    dfs(1,0);
    for(int t = 1;t <= 20;++t){
        for(int i = 1;i <= n;++i){
            pa[i][t] = pa[pa[i][t-1]][t-1];
        }
    }
    for(int u = 1;u <= n;++u) for(int v : B[u]){
        mk[v] ++,mk[u] ++,mk[lca(u,v)] -= 2;
    }

    dfs2(1,0);

}
signed main()
{
    ios::sync_with_stdio(false);
    n = getint();
    int u,v;
    for(int i = 0;i < n-1;++i) {
        u = getint();v = getint();
        A[u].push_back(v);
    }
    for(int i = 0;i < n-1;++i) {
        u = getint(),v = getint();
        B[u].push_back(v);
    }

    solve(A,B);


    if(mi == 2) return 0*printf("%d %d\n",mi,ans);

    solve(B,A);

    cout<' '<return 0;
}