【文章阅读】SA-SSD
Brief
来自CVPR2020的研究工作,也是仅仅使用Lidar数据进行3D检测的文章,CVPR2020接收的几篇文章中,采用LiDar作为网络结构输入的已经已经多于采用图像和lidar的结合,从一方面讲,lidar数据由于包含了现实场景中的几何结构而比双目信息包含更加精确的信息。同时受到的外界条件的影响也相应的越小。
这是一篇来自 港理工和阿里达摩院的合作文章。
这里是 paper
这里是 code
核心创新和主要内容
本文核心创新是想要将二阶段方法独有精细回归运用在一阶段的的检测方法上,为此作者采用了SECOND作为backbone,添加了两项附加任务,使得backbone具有structure aware的能力,定位更加准确;此外在一阶段中存在预测框和cls maps之间不匹配的问题,本文也设计了一种策略解决这个问题。
Abstract
- 3D检测中的one stage的检测方法都是通过卷积逐步缩小fea-map,没有上采样过程,这样会导致空间信息的丢失,无法用几何结构,对定位精度降低比较明显.
20年前的one-stage的方法都是voxel-based的方法,主要思想都是场景体素化、3D卷积(稀疏卷积)降低到二维,再采用二维 RPN head,拿SECOND1.5举例,整个过程是从1280108040到1601321的逐步向下卷积的过程。
20年的另外一片CVPR 3D-SSD则是第一个point-based 的一阶段的检测方法,同时是anchor-free的。
- 本文中心在通过深度挖掘三维物体的几何信息来提高定位精度。
以前的研究工作都是point to tensor的,而这里作者为了将卷积得到的信息用点结构表达,设计了一个auxiliary network,用于将Tensor信息转化到point上,因为piont实际上是还保留着原始的几何结构,这里作者可能是想将语义信息和细节信息融合。
- 这个辅助网络和backbone是一同训练的,引导backbone感知object structure
这一点和pointnet的两个辅助网络也挺像的,pointnet中的作用是使得网络可以感知问题的刚体变换。
- 辅助网络在推理阶段不参与运算,可以和主干网络分离,因此不会增加额外运算量
- 作者提出第二个问题是:一阶段的方法会在cls 置信度和对应的预测框之间存在不一致的问题,所以本文提出了一个方法将置信度和bbox对齐。
1. Introduction
auxiliary network
这是作者提出的解决的第一个问题,如下图的对比中,(a)图是SECOND检测出的bbox,可以看出在object 点比较少的时候虽然也可以检出,但是对应的框的定位效果就不如本文提出的(b)的实验效果。
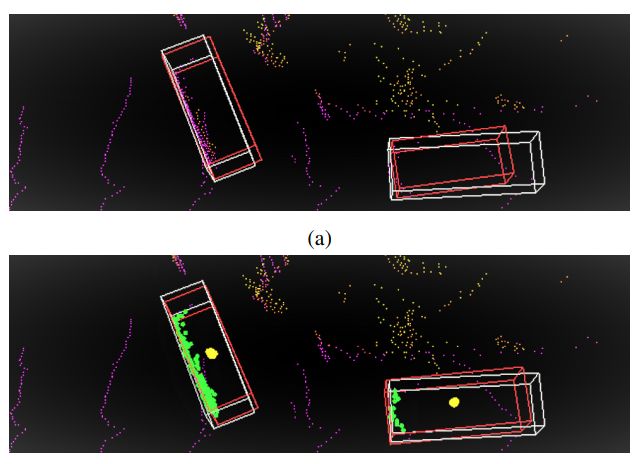
这一问题仅仅在One-stage的检测方法中会出现,因为two-stage第一步提出proposals后,在第二步会精细的在fea map上进行精细的回归,所以在19年ICCV的文章主要的研究点则是 onestage的方法转two-stage,精度也是有很大的提升。但是不可避免的在时间消耗上增大,这也从侧面验证了利用细粒度信息对精细回归的重要性。
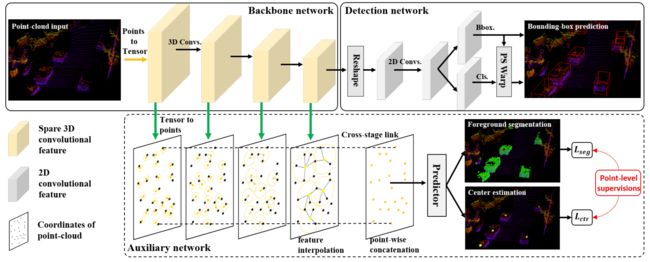
所以本文作者的核心第一个问题是将二阶段使用的精细回归的细粒度信息如何附加到一阶段信息中,也就是作者提出的如下的网络结构,可以看的出来作者的核心创新点在下面的auxiliary的网络结构中。该结构可以监督上层的tensor表达的学习到点云中的几何结构信息。
该附加网络结构做了如下几个操作:
- 将feature 转化到point的上,得到point-wise的特征信息
- 前景分割,目的是使得该网络结构对边界敏感,同时point-wise的特征估计object 中心加大内点感知能力。
feature map warping method
这就是作者提出的第二个问题,在one-stage的方法中,由于没有精细的回归会导致最后分类时得到的分数不太好,这会影响后续的NMS工作,因此作者设计了一个Align的方法,使得输出的分类置信度更具有可信度。
前人研究
One -tage approaches
一阶段的方法从Voxelnet开始后续很多工作都是一阶段的,SECOND ,PointPillars都是经典的一阶段方法。
Two-stage approaches
两阶段的方法可以从point-based和voxel-based的方法上进行分说。
除去CVPR20的3D-SSD这篇文章,之前的基本所有的Pointbased的方法都是多阶段的,其中比较出名的工作有CVPR18的F-pointnet,这篇工作是先通过二维检测得到检出的目标,再通过视锥投影到三维点云中,最后采用pointnet的变体结构进行定位和分类,实际上算作是三阶段的方法;后续的IROS19的F-ConvNet在F-pointnet的基础上将投影出来的视锥中的点云根据距离划分为多个序列。在同年的CVPR19上Point-Rcnn 也是point-based的目标检测方法,不过是Lidar-only的方法,以每一个点为anchor预测和回归目标框,计算消耗比较大。
针对Voxel-based的方法,在19年上后半段有挺多著名的工作,Fast-Point-RCNN,STD,PartA^2等等工作,也就是在前人的单阶段的基础上加入了refine的网络模块,进一步优化了定位。
除此之外,融合图像信息和Lidar信息在19年及之前是很流行的,不过最新的方法几乎都是LIDAR-only的方法了,比较近的有AAAI20的PIRCNN,这一篇也是一个两阶段的方法,通过lidar预测出的框和图像特征融合做二阶段的回归。
Auxiliary task learning
- 这个子话题的主要思想是:
通过附加任务使得backbone具有某种特征倾向的能力。作者在本文中添加了两个point-wise prediction tasks目的是提高3D检测的结果,如上图展示的那样,增加了前景分割和中心预测两个任务;但是本文的附加任务在推理阶段是可以被舍弃的,不增加额外的计算量。 - Point-wise feature representation
如上图所示的那样,本文中需要把Backbone的tensor特征转化到point为载体上, { ( f j , p j ) : j = 1 , … , M } \left\{\left(f_{j}, p_{j}\right): j=1, \ldots, M\right\} {(fj,pj):j=1,…,M}表示坐标为 p j p_j pj的点的特征为 f j f_j fj,由于在最开始原始点云转化为tensor输入时会丢失一些局部点(后文讲到),所以从tensor-到point时是一对多的特征,如果采用retrail的方式,那么相邻点的特征都是一样的,作者这里采用的是FP层,即是插值的方式, { ( f ^ i , p i ) : i = 1 , … , N } \left\{\left(\hat{f}_{i}, p_{i}\right): i=1, \ldots, N\right\} {(f^i,pi):i=1,…,N}表示为经过FP层的特征信息,采用以下公式得到插值后的特征:
f ^ i = ∑ j = 1 M w j ( p i ) f j ∑ j = 1 M w j ( p i ) \hat{f}_{i}=\frac{\sum_{j=1}^{M} w_{j}\left(p_{i}\right) f_{j}}{\sum_{j=1}^{M} w_{j}\left(p_{i}\right)} f^i=∑j=1Mwj(pi)∑j=1Mwj(pi)fj
其中:
w j ( p i ) = { 1 ∥ p i − p j ∥ 2 if p j ∈ N ( p i ) 0 otherwise w_{j}\left(p_{i}\right)=\left\{\begin{array}{ll} \frac{1}{\left\|p_{i}-p_{j}\right\|_{2}} & \text { if } p_{j} \in \mathcal{N}\left(p_{i}\right) \\ 0 & \text { otherwise } \end{array}\right. wj(pi)={∥pi−pj∥210 if pj∈N(pi) otherwise
从上式插值的方式可以看出,采用距离作为权重进行加权。这里的 N ( p i ) \mathcal{N}\left(p_{i}\right) N(pi)设置为0.05的球体,这也和后面的point 到tensor的设置对应,采用的是(0.05,0.05,0.1)的尺度划分voxel。
最后再将多层voxel到point的特征concat一起。 - Auxiliary tasks
前景分割任务监督loss:
L s e g = 1 N p o s ∑ i N − α ( 1 − s ^ i ) γ log ( s ^ i ) \mathcal{L}_{\mathrm{seg}}=\frac{1}{N_{p o s}} \sum_{i}^{N}-\alpha\left(1-\hat{s}_{i}\right)^{\gamma} \log \left(\hat{s}_{i}\right) Lseg=Npos1i∑N−α(1−s^i)γlog(s^i)
where
s ^ i = { s ~ i if s i = 1 1 − s ~ i otherwise \hat{s}_{i}=\left\{\begin{array}{ll} \tilde{s}_{i} & \text { if } s_{i}=1 \\ 1-\tilde{s}_{i} & \text { otherwise } \end{array}\right. s^i={s~i1−s~i if si=1 otherwise
如上式的表达式,采用的为focal loss.
object 中心预测loss:
L c t r = 1 N p o s ∑ i N Smooth − l 1 ( Δ p ~ − Δ p ) ⋅ 1 [ s i = 1 ] \mathcal{L}_{\mathrm{ctr}}=\frac{1}{N_{p o s}} \sum_{i}^{N} \operatorname{Smooth}-l_{1}(\Delta \tilde{\mathbf{p}}-\Delta \mathbf{p}) \cdot \mathbb{1}\left[s_{i}=1\right] Lctr=Npos1i∑NSmooth−l1(Δp~−Δp)⋅1[si=1]
如上式采用的是smooth-l1损失函数,对残差进行回归。
网络结构
Backbone
- input representation
以前的onestage的方法采用对整个场景进行volize化,但是这个过程是一个很消耗时间的,作者为了简化这个过程,采用了如下的方法:
输入的点云可以表示为 { p i = ( x i , y i , z i ) : i = 1 , … N } \left\{p_{i}=\left(x_{i}, y_{i}, z_{i}\right): i=1, \ldots N\right\} {pi=(xi,yi,zi):i=1,…N},为了量化点云,作者假设点云场景的单位长度为 d = [ d x , d y , d z ] d=\left[d_{x}, d_{y}, d_{z}\right] d=[dx,dy,dz],所以量化后的点云输入为: { p ˉ i = ( ⌊ x i d x ⌋ , ⌊ y i d y ⌋ , ⌊ z i d z ⌋ ) \left\{\bar{p}_{i}=\left(\left\lfloor\frac{x_{i}}{d_{x}}\right\rfloor,\left\lfloor\frac{y_{i}}{d_{y}}\right\rfloor,\left\lfloor\frac{z_{i}}{d_{z}}\right\rfloor\right)\right. {pˉi=(⌊dxxi⌋,⌊dyyi⌋,⌊dzzi⌋)这里表示的是向下取整。并且如果遇到不同的点采用了同样的索引,那么更新为最新的输入就可以了,在实验中作者设置的尺度大小为 d = [ 0.05 m , 0.05 m , 0.1 m ] d=[0.05 \mathrm{m}, 0.05 \mathrm{m}, 0.1 \mathrm{m}] d=[0.05m,0.05m,0.1m]
和SECOND1.5后我们知道,SECOND1.5是采用的尺度信息也是这么大,不过SECOND架构为了实现更多的框架,设置的在每一个voxel中最大的点个数只有5,就类似本文中作者设置的1一个意思。在SECOND1.5中对每一个voxel实际上也没有沿用VoxelNet中的那样采用MLP进行特征提取,而是直接取平均值;所以本文作者这样做实际上效果是一样的,只是预处理会更快。
- Network architecture
本文作者的backobne实际上和SECONDE的一脉相承,不过本文作者在to point的表示上的时候采用的multi-level特征连接,采用稀疏卷积到BEV feamap,最后也采用标准的二维卷积预测最后的anchor,本文采用的是ancor_based head。
- Auxiliary
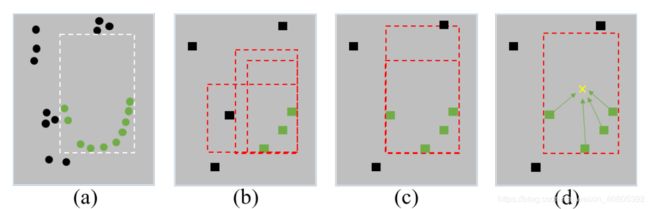
也就是在前文中笔者提到的两个问题,第一点,目前的onestage的方法一直下采样会导致空间信息的模糊和丢失,会导致后面的detection过程的定位不准,这里如下图中的含义,其中a表示最原始的bbox,背景点和前景点;通过多次卷积stride过程会导致如图(b)所示的问题,有些比较偏远的前景点特征融合为了背景信息。
作者针对第一个问题提出了辅助网络,将从Muti-level的voxel特征融合在监督训练,使得backbaone的网络结构具有structure aware的能力。
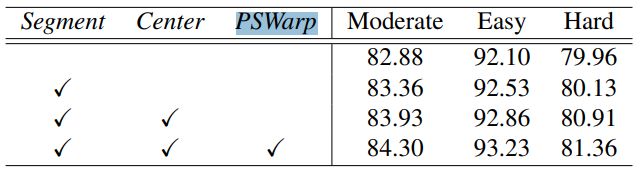
下图中的图©表示的是在添加了前景分割的附加任务,但是不添加中心点预测的检测结果,进一步的图(d)表示添加上述两项附加任务后的检测结果。
- Part-sensitive warping
这里是为了解决作者所提出的第二个问题,the misalignment between the predicted bounding boxes and corresponding confidence maps。这也是one stage 都会存在的一个问题。
具体操作如下:
(1)首先修改分类的最后一层用于生成K个 part-sensitive 的 cls maps,记做 { X k : k = 1 , 2 , … , K } \left\{\mathcal{X}^{k}: k=1,2, \ldots, K\right\} {Xk:k=1,2,…,K},这里边的每一块包含着object的部分信息,例如K=4时的信息可以理解为{upper-left, upper-right, bottom-left, bottom-right},同时对Bbox的每一个fea map 都划分为K个子窗口,并且选择每个窗口的中心为采样点。这样作者就得到了K个采样的格点记做 { S k : k = 1 , 2 , … , K } \left\{\mathcal{S}^{k}: k=1,2, \ldots, K\right\} {Sk:k=1,2,…,K},分别对用这上述的cls map。
(2)步骤(1)中的得到的cls map和格点一同送入PSWarp结构,如下图,该sampler的输出是格点对应的cls map的特征
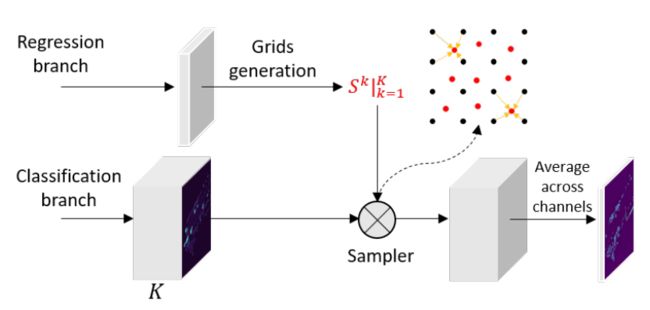
(3)最终的输出是多个采样后的cls maps的平均值
损失函数
本文采用的是anchor -based的方法,其损失函数和以往的voxel-based的方法一致,只是多了上述提到的附加任务的两项损失。如下:
L = L c l s + ω L b o x + μ L s e g + λ L c t r \mathcal{L}=\mathcal{L}_{\mathrm{cls}}+\omega \mathcal{L}_{\mathrm{box}}+\mu \mathcal{L}_{\mathrm{seg}}+\lambda \mathcal{L}_{\mathrm{ctr}} L=Lcls+ωLbox+μLseg+λLctr
实验
实现细节
笔者只提一下本文使用的数据增广方案,也是采用的先将所有object收集起来再随机变换后放置在训练集中,都是源自SECOND的方法。
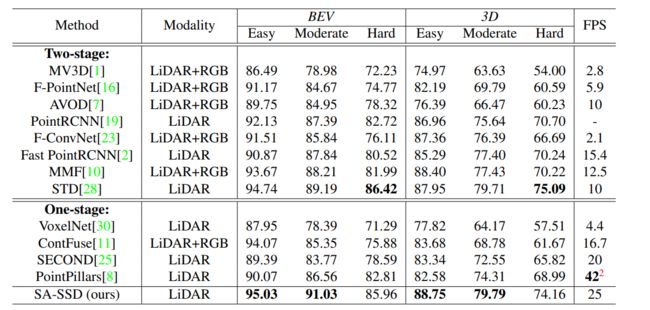
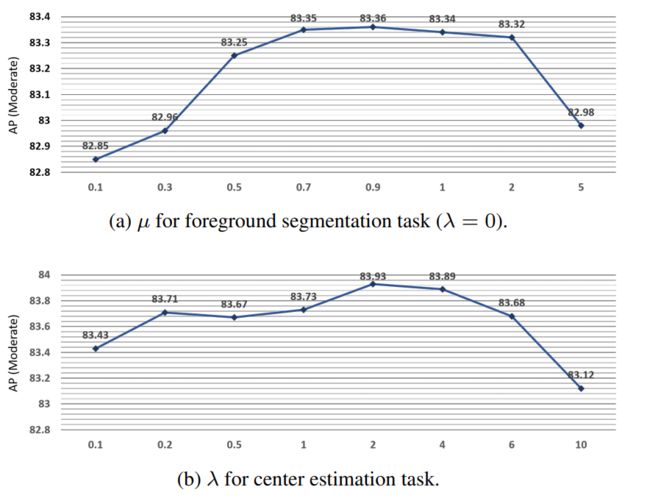
附加任务参数影响
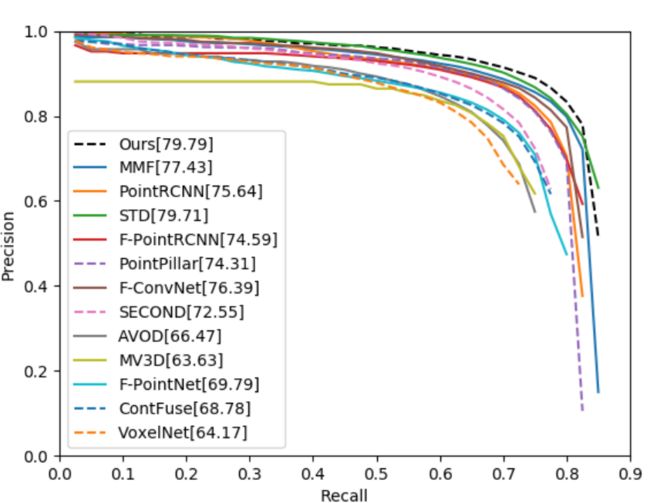
precision-recall
在KIITI的test数据集上,作者画出了对应的精度-召回率曲线(在KITTI官网上有)