优化器(Optimization)
优化器(Optimization)
- SGD(Stochastic Gradient Descent)
- SGD +Momentum
- Nesterov Momentum
- AdaGrad
- RMSProp
- Adam
SGD(Stochastic Gradient Descent)
x t + 1 = x t − α ∇ f ( x t ) x_{t+1}=x_t-\alpha\nabla f(x_t) xt+1=xt−α∇f(xt)
While True:
Weights_grads = evaluate_gradient(loss_fun,data,weights)
Weights += -step_size*weights_grad

目标找到最深的红色区域
在这种情况下,首先评估一些小批数据中的损失的梯度,更进一步,向梯度为负的方向更新参数向量,因为他给出了损失函数下降最快的方向,然后重复这个过程,最后在红色部分收敛
存在问题:
如果损失在一个方向上变化很快而在另一个方向变化缓慢呢?
梯度下降有什么作用?
当在水平方向改变值,损失函数变化非常慢,在等高线图上下运动时,损失值则对竖直方向的变化非常敏感。
这一点是海森矩阵中最大与最小奇异值之比
沿低维进展非常缓慢,沿高维方向抖动
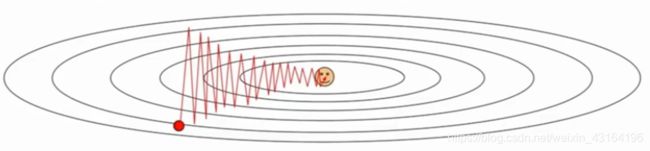
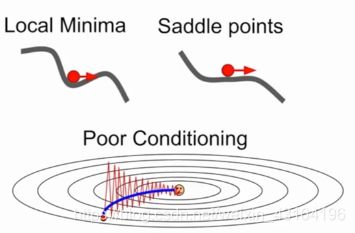
损失函数具有高条件数:比率Hessian矩阵的最大到最小奇异值很大。
问题2:局部极小值或鞍点

问题3:随机性 存在噪声
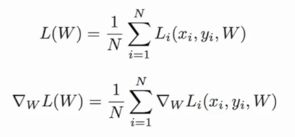
N是训练数据集
SGD +Momentum
v t + 1 = ρ v t + ∇ f ( x t ) v_{t+1}=ρv_t+ \nabla f(x_t) vt+1=ρvt+∇f(xt)
x t + 1 = x t − α v t + 1 x_{t+1}=x_t-\alpha v_{t+1} xt+1=xt−αvt+1
vx = 0
while True:
dx = compute_gradient(x)
vx = rho*vx+dx
x += learning_rate * vx
思想:保持一个不随时间变化的速度,并且将速度估计添加到这个速度上,然后在这个速度的方向上步进,而不是在梯度的方向上步进。
含有和摩擦(rho)有关的超参数ρ,在每一步,采用当前的速度,然后用摩擦系数ρ来对其衰减,之后加到梯度上,现在我们在速度向量的方向上步进,而不是在原始梯度的方向上步进。摩擦系数有时取值比较大,例如0.9,0.99
解决了SGD存在的问题:
Nesterov Momentum
v t + 1 = ρ v t − α ∇ f ( x t + ρ v t ) v_{t+1}=ρv_t- \alpha \nabla f( \bf{x_t+ρv_t} ) vt+1=ρvt−α∇f(xt+ρvt)
x t + 1 = x t + v t + 1 x_{t+1}=x_t+v_{t+1} xt+1=xt+vt+1
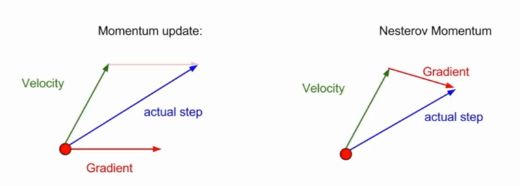
前者:估算当前位置的梯度,然后取速度和梯度的混合
Nesterov Momentum:从红色点开始,然后取得的速度的方向上进行步进,之后,评估这个位置的梯度,随后回到初始位置,将这两者混合起来
改进公式:
x ~ t = x t + ρ v t \tilde{x}_{t} =x_t+ρv_t x~t=xt+ρvt
v t + 1 = ρ v t − α ∇ f ( x ~ t ) v_{t+1}=ρv_t-\alpha\nabla f( \tilde{x}_{t} ) vt+1=ρvt−α∇f(x~t)
x t + 1 = x ~ t − ρ v t + ( 1 + ρ ) v t + 1 = x ~ t + v t + 1 + ρ ( v t + 1 − v t ) x_{t+1}=\tilde{x}_{t}-ρv_t+(1+ρ)v_{t+1} =\tilde{x}_{t}+v_{t+1}+ρ(v_{t+1}-v_{t}) xt+1=x~t−ρvt+(1+ρ)vt+1=x~t+vt+1+ρ(vt+1−vt)
dx = compute_gradient(x)
old_v = v
v = rho * v - learning_rate * dx
x += -rho * old_v + (1+rho) * v
Nesterov梯度下降会预知你的下一步将会时到坡的对面去,所以会提示你提前刹车,避免过度冲到坡的对面去
含有矫正因子,不会剧烈的越过局部极小值点。
AdaGrad
思想 : 在优化过程中,需要保持一个在训练过程中的每一步的梯度的平方和的持续估计。与速度项不同的是,我们有了一个梯度平方项。在训练过程中我们会一直累加当前梯度的平方到这个梯度平方项,当更新参数向量时,会除以这个梯度平方项
grad_squared = 0
while True:
dx = compute_gradient(x)
grad_squared += dx * dx
x -= leraning_rate * dx / (np.sqrt(grad_squared) + 1e-7)
这样的放缩对于矩阵中条件数很大的情形的改进:
如果我们有两个坐标轴,沿其中一个轴有很高的梯度,而另一个轴方向却有很小的梯度,那么随着累加小梯度的平方,会在最后更新参数向量时除以一个很小的值,从而加速了在小梯度维度上的学习速度;在另一个维度方向上,由于梯度变得特别大,会除以一个非常大的数,会降低这个维度方向上的训练进度。
存在问题:
当时间t越来越大时,在训练过程中使用AdaGrad步长会变得越来越小,因为一直在随时间更新梯度平方的估计值,所以这个估计值在训练过程中一直随时间单调递增,这会导致步长随着时间越来越小。在学习目标是一个凸函数的情况下有理论证明这个特征效果很好。因为当接近极值点时,会逐渐的慢下来最后到达收敛。在非凸函数的情况下,会变得复杂,因为当到达一个局部的极值点时,使用AdaGrad会被困住,从而使得训练过程无法在进行下去
RMSProp
grad_squared = 0
while True:
dx = compute_gradient(x)
grad_squared = decay_rate *grad_squared + (1 - decay_rate) * dx * dx #decay_rate为0.9或0.99
x -= leraning_rate * dx / (np.sqrt(grad_squared) + 1e-7)
是AdaGrad的一个变体,依然计算梯度的平方,但是并不是仅仅简单的在训练中累加梯度平方,而是会让平方梯度按照一定比率下降。在计算完梯度以后,取出当前梯度的平方,将其乘以一个衰减率,通常为0.9或0.99,然后用1减去衰减率乘以梯度平方,加上之前的结果,随着训练的进行,步长和AdaGrad一样,步长在被除了平方梯度之后,会有一个良好的性质,在一个维度上(梯度下降很慢的)训练会加快,而在另一个维度方向上训练减慢。由于梯度平方估计被衰减了,有可能会造成训练总是一直在变慢
Adam
first_moment = 0
second_moment = 0
while True:
dx = compute_gradient(x)
first_moment = beta1 * first_moment + (1 - beta1) * dx #Momentum
second_moment = beta2 * second_moment + (1-beta2) * dx * dx #AdaGrad/RMSProp
x -= learning_rate * first_moment / (np.sqrt(second_moment) + 1e-7)) #AdaGrad/RMSProp
更新第一动量和第二动量的估计值,让第一动量的估计值等于梯度加权和,
有一个第二动量的动态估计值,是梯度平方的动态近似值
存在问题:
在最初的第一步,将第二动量初始值设为0,经过一步更新后,由于beta2第二动量衰减率接近于1,经过一次更新,第二动量仍然非常接近于0,在作出更新步骤,除以第二动量,也就是一个非常小的数,那么在一开始就会得到一个很大的步长,这并不是因为这一步的梯度太大,而是因为人为的将第二动量初始化成了0。
增加了偏置校正项来避免出现开始时得到很大的步长问题的出现
#full form
first_moment = 0
second_moment = 0
for t in range(num_iterations):
dx = compute_gradient(x)
first_moment = beta1 * first_moment + (1 - beta1) * dx #Momentum
second_moment = beta2 * second_moment + (1-beta2) * dx * dx #AdaGrad/RMSProp
first_unbias = first_moment / (1 - bata1 ** t) #Bias correction
second_unbias = second_moment / (1 - bata2 ** t) #Bias correction
x -= learning_rate * first_moment / (np.sqrt(second_moment) + 1e-7)) #AdaGrad/RMSProp
Adam参数初始值:beta1=0.9 beta2=0.999 learning_rate=1e-3 or 5e-4