【机器学习算法】【三】贝叶斯模型
一. 离散型随机变量和连续型随机变量
首先需要先了解基本的概率论知识,由于自己太长时间没有接触概率知识,所以忘记的差不多了,现在需要回忆一下。
- 概率相关知识
-
离散型随机变量:如果随机变量X只可能取有限个或可列个值x1,x2,…,,则称X为离散型随机变量。
离散变量是指其数值只能用自然数或整数单位计算的则为离散变量.例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用 计数方法取得. -
连续型随机变量:这种变量的取值充满一个区间,无法一一排出。
连续随机变量,在一定区间内可以任意取值的变量,其数值是连续不断的.,相邻两个数值可作无限分割,即可取无限个数值.例如, 生产零件 的 规格尺寸 , 人体测量 的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得.
在数学中,连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。概率密度函数一般以小写标记。
参考:常见的连续性随机变量的常见分布
二. 贝叶斯理论的思想
掷硬币的例子说明了古典统计学的思想,就是概率是基于大量实验的,也就是 大数定理。那么现在再问你,有些事件,例如:明天下雨的概率是30%;A地会发生地震的概率是5%;一个人得心脏病的概率是40%…… 这些概率怎么解释呢?难道是A地真的100次的机会里,地震了5次吗?肯定不是这样,所以古典统计学就无法解释了。再回到掷硬币的例子中,如果你没有机会掷1000次这么多次,而是只掷了3次,可这3次又都是正面,那该怎么办?难道这个正面的概率就是100%了吗?这也是古典统计学的弊端。
举一个具体的例子:
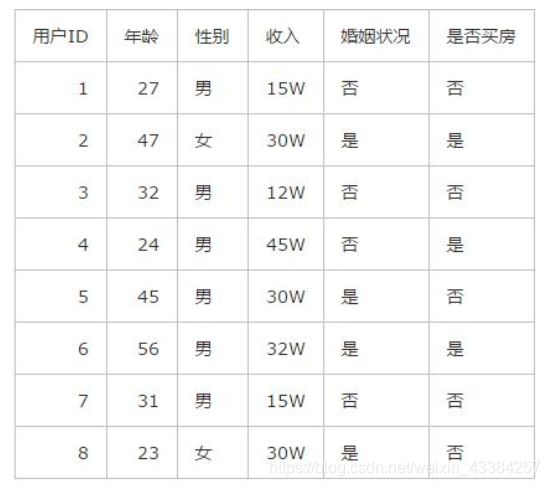
如果你在一家购房机构上班,今天有8个客户来跟你进行了购房沟通,最终你将这8个客户的信息录入了系统之中:
此时又有一个客户走了进来,经过交流你得到了这个客户的信息:
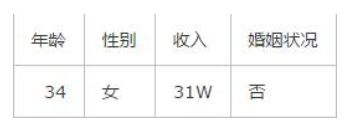
那么你是否能够判断出这位客户会不会买你的房子呢?
如果你没有接触过贝叶斯理论,你就会想,原来的8个客户只有3个买房了,5个没有买房,那么新来的这个客户买房的意愿应该也只有3/8 。
这代表了传统的频率主义理论,就跟抛硬币一样,抛了100次,50次都是正面,那么就可以得出硬币正面朝上的概率永远是50%,这个数值是固定不会改变的。例子里的8个客户就相当于8次重复试验,其结果基本上代表了之后所有重复试验的结果,也就是之后所有客户买房的几率基本都是3/8 。
但此时你又觉得似乎有些不对,不同的客户有着不同的条件,其买房概率是不相同的,怎么能用一个趋向结果代表所有的客户呢?
对了!这就是贝叶斯理论的思想,简单点讲就是要在已知条件的前提下,先设定一个假设(买或者不买),然后通过先验实验(前提条件)来更新这个概率,每个不同的实验都会带来不同的概率。
参考:数据分析经典模型——贝叶斯理论
三. 概率基础知识
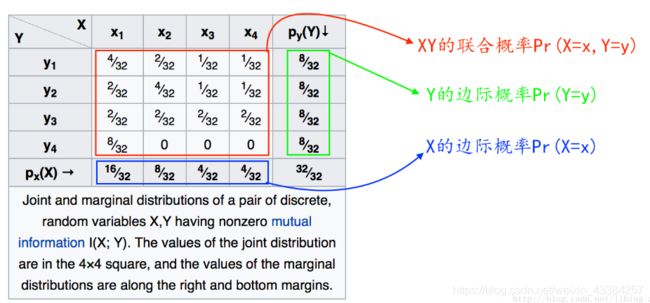
联合概率、边际概率、条件概率
- P r ( X = x , Y = y ) Pr(X=x, Y=y) Pr(X=x,Y=y) 为“XY的联合概率”,表示两个事件同时发生的概率。
- P r ( X = x ) Pr(X=x) Pr(X=x) 为“X的边际概率”,可以看出某一个边际概率等于这一列所有联合概率的发生的概率和
- P r ( X = x ∣ Y = y ) Pr(X=x | Y=y) Pr(X=x∣Y=y) 为“X基于Y的条件概率”
- P r ( Y = y ) Pr(Y=y) Pr(Y=y) 为“Y的边际概率”
从上式子中可以看到:
P r ( X = x , Y = y ) = P r ( X = x ∣ Y = y ) ∗ P r ( Y = y ) Pr(X=x, Y=y) = Pr(X=x | Y=y) * Pr(Y=y) Pr(X=x,Y=y)=Pr(X=x∣Y=y)∗Pr(Y=y)
P r ( X = x 1 ) = P r ( X = x 1 , Y = y 1 ) + P r ( X = x 1 , Y = y 2 ) + P r ( X = x 1 , Y = y 3 ) + P r ( X = x 1 , Y = y 4 ) Pr(X=x_1)=Pr(X=x_1,Y=y_1)+Pr(X=x_1,Y=y_2)+Pr(X=x_1,Y=y_3)+Pr(X=x_1,Y=y_4) Pr(X=x1)=Pr(X=x1,Y=y1)+Pr(X=x1,Y=y2)+Pr(X=x1,Y=y3)+Pr(X=x1,Y=y4)
即: X Y 的 联 合 概 率 = X 基 于 Y 的 条 件 概 率 ∗ Y 的 边 际 概 率 XY的联合概率=X基于Y的条件概率*Y的边际概率 XY的联合概率=X基于Y的条件概率∗Y的边际概率
x 1 边 际 概 率 = x 1 这 一 列 所 有 联 合 概 率 之 和 , 把 所 有 y 的 取 值 取 尽 x_1边际概率 = x_1这一列所有联合概率之和,把所有y的取值取尽 x1边际概率=x1这一列所有联合概率之和,把所有y的取值取尽
这个就是联合概率、边际概率、条件概率之间的转换计算公式。
前面表述的是离散分布,对于连续分布,也差不多。 只需要将“累加”换成“积分”。

参考:贝叶斯及其相关基础知识
1. 条件概率
最基本的高中(初中)的知识,我们用 P ( A ∣ B ) P(A|B) P(A∣B)来表示,在事件B已经发生的前提下,事件A发生的概率。
若AB之间存在一定的关联性,则我们可以知道:
P ( A ∣ B ) = P ( A , B ) P ( B ) P(A|B) = \frac{P(A,B)}{P(B)} P(A∣B)=P(B)P(A,B)
若事件AB为独立事件,则我们可以知道:
P ( A ∣ B ) = P ( A ) P(A|B) = P(A) P(A∣B)=P(A)
- 也可以看出: 联 合 概 率 = 条 件 概 率 ∗ 边 际 概 率 联合概率=条件概率*边际概率 联合概率=条件概率∗边际概率
P ( A , B ) = P ( A ∣ B ) ∗ P ( B ) = P ( B ∣ A ) ∗ P ( A ) P(A,B)=P(A|B)*P(B)=P(B|A)*P(A) P(A,B)=P(A∣B)∗P(B)=P(B∣A)∗P(A) - 某 一 个 边 际 概 率 = 这 个 边 际 概 率 所 在 列 的 所 有 联 合 概 率 的 和 某一个边际概率 = 这个边际概率所在列的所有 联合概率的和 某一个边际概率=这个边际概率所在列的所有联合概率的和
P ( A = a ) = P ( A = a , B = b 1 ) + P ( A = a , B = b 2 ) + . . . . . . . P ( A = a , B = b j ) P(A=a)=P(A=a,B=b_1)+P(A=a,B=b_2)+.......P(A=a,B=b_j) P(A=a)=P(A=a,B=b1)+P(A=a,B=b2)+.......P(A=a,B=bj)
2. 贝叶斯定理
贝叶斯公式:
P ( A i ∣ B ) = P ( A i , B ) P ( B ) = P ( A i ) P ( B ∣ A i ) ∑ j = 1 n P ( A j ) P ( B ∣ A j ) P(A_i|B) =\frac{P(A_i,B)}{P(B)}= \frac{P(A_i)P(B|A_i)} {\sum_{j=1}^{n}P(A_j)P(B|A_j)} P(Ai∣B)=P(B)P(Ai,B)=∑j=1nP(Aj)P(B∣Aj)P(Ai)P(B∣Ai)
P ( A i , B ) P(A_i,B) P(Ai,B)为联合概率,可以交换顺序求得
P ( B ) P(B) P(B)为边际概率,可以将所有A的取值取尽,联合概率之和,然后联合概率还是等于交换顺序。
3. 条件独立
条件独立的性质能用于简化模型的参数,其最基本的形式可以表达为:
P ( B C ∣ A ) = P ( B ∣ A ) ∗ P ( C ∣ A ) P(BC|A) = P(B|A)*P(C|A) P(BC∣A)=P(B∣A)∗P(C∣A)
ABC都相互独立。
四. 贝叶斯模型原理流程理解
朴素贝叶斯的分类方法其实就是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练集合,首先基于特征条件独立(朴素由此而来)学习输入,输出的联合概率分布,然后基于学到的,对给定的输入,利用贝叶斯定理求出后验概率最大的输出。把上面的贝叶斯定理,运用在分类问题上,我们可以得到一个浅显易懂的式子:
P ( 类 别 ∣ 特 征 ) = P ( 特 征 ∣ 类 别 ) P ( 类 别 ) P ( 特 征 ) P(类别|特征) = \frac{P(特征|类别)P(类别)} {P(特征)} P(类别∣特征)=P(特征)P(特征∣类别)P(类别)
至此,大家应该对该模型有了一个初步的理解印象。
假设我们的训练集合为,
D a t a = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . . . ( x i , y i ) Data = {(x_1,y_1),(x_2,y_2),.....(x_i,y_i)} Data=(x1,y1),(x2,y2),.....(xi,yi)
其中x为 N N N维的向量(即每个输入,都有N维特征),且输入样本之间无干扰,独立分布;输出样本 Y = c 1 , c 2 , . . . , c k Y = {c_1, c_2, ..., c_k} Y=c1,c2,...,ck。
则根据上述的贝叶斯公式,我们可以计算得出:
P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( X = x ∣ Y = c k ) P ( Y = c k ) P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)} {\sum_k P(X=x|Y=c_k)P(Y=c_k)} P(Y=ck∣X=x)=∑kP(X=x∣Y=ck)P(Y=ck)P(X=x∣Y=ck)P(Y=ck)
当输入的特征是 X = x X = x X=x的时候求输出结果是 Y = c k 的 概 率 Y=c_k的概率 Y=ck的概率
- P ( Y = c k , X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) = P ( Y = c k ∣ X = x ) P ( X = x ) P(Y=c_k,X=x)=P(X=x|Y=c_k)P(Y=c_k)=P(Y=c_k|X=x)P(X=x) P(Y=ck,X=x)=P(X=x∣Y=ck)P(Y=ck)=P(Y=ck∣X=x)P(X=x)
因为你我们要求 P ( Y = c k ∣ X = x ) P(Y=c_k|X=x) P(Y=ck∣X=x)所以用第一个公式。- P ( X = x ) = P ( X = x , Y = c 1 ) + P ( X = x , Y = c 2 ) + . . . . . + P ( X = x , Y = c k ) P(X=x)=P(X=x,Y=c_1)+P(X=x,Y=c_2)+.....+P(X=x,Y=c_k) P(X=x)=P(X=x,Y=c1)+P(X=x,Y=c2)+.....+P(X=x,Y=ck)
因此,我们的预测分类即为:
y = a r g m a x c k P ( Y = c k ∣ X = x ) y = argmax _{c_k}P(Y=c_k|X=x) y=argmaxckP(Y=ck∣X=x)
而对于所有的分类概率来说,其分母都是一致的,所以简写为:
y = a r g m a x c k P ( X = x ∣ Y = c k ) P ( Y = c k ) y = argmax _{c_k}P(X=x|Y=c_k)P(Y=c_k) y=argmaxckP(X=x∣Y=ck)P(Y=ck)
各个特征之间满足条件独立的假设 X = x 1 , x 2 . . . . . x n X={x_1,x_2.....x_n} X=x1,x2.....xn,因此,上式又可以简化为:
y = a r g m a x c k P ( Y = c k ) ∏ N P ( x j ∣ Y = c k ) y = argmax _{c_k}P(Y=c_k)\prod_N P(x^j|Y=c_k) y=argmaxckP(Y=ck)N∏P(xj∣Y=ck)
至此,整套朴素贝叶斯模型就结束了。
总结:
最重要的就是两个公式:
一个是求联合概率的:
P ( A , B ) = P ( A ∣ B ) ∗ P ( B ) = P ( B ∣ A ) ∗ P ( A ) P(A,B)=P(A|B)*P(B)=P(B|A)*P(A) P(A,B)=P(A∣B)∗P(B)=P(B∣A)∗P(A)
一个是求边际概率的:
P ( A = a ) = P ( A = a , B = b 1 ) + P ( A = a , B = b 2 ) + . . . . . . . P ( A = a , B = b j ) P(A=a)=P(A=a,B=b_1)+P(A=a,B=b_2)+.......P(A=a,B=b_j) P(A=a)=P(A=a,B=b1)+P(A=a,B=b2)+.......P(A=a,B=bj)
参考:
贝叶斯及其相关基础知识
朴素贝叶斯分类模型
数据分析经典模型——贝叶斯理论