Pytorch中的优化器optimizer
文章目录
- 一、Pytorch中常见的optimizer
- 1、torch.optim.SGD
- SGD+Momentum
- Nesterov Momentum
- 2、 torch.optim.ASGD
- 3、 torch.optim.Rprop
- 4、 torch.optim.Adagrad
- 5 、torch.optim.Adadelta
- 6、 torch.optim.RMSprop
- 7 、torch.optim.Adam(AMSGrad)
- 8 、torch.optim.Adamax
- 9、 torch.optim.SparseAdam
- 10、 torch.optim.LBFGS
- 二、不同优化器的比较
- 三、直观看不同优化方法的动态学习过程
- 参考博客:
结合PyTorch中的optimizer谈几种优化方法。方法分为2大类:一大类方法是SGD及其改进(加Momentum);另外一大类是Per-parameter adaptive learning rate methods(逐参数适应学习率方法),包括AdaGrad、RMSProp、Adam等。
一、Pytorch中常见的optimizer
1、torch.optim.SGD
当训练数据N很大时,计算总的cost function来求梯度代价很大,所以一个常用的方法是计算训练集中的小批量(minibatches),这就是SGD。
minibatch的大小是一个超参数,通常使用2的指数,是因为在实际中许多向量化操作实现的时候,如果输入数据量是2的倍数,那么运算更快。
SGD的缺点:
(1)Very slow progress along shallow dimension, jitter along steep direction
(2)到local minima 局部极小值或者saddle point鞍点会导致gradient为0,无法移动。而事实上,saddle point问题在高维问题中会更加常见。
class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
功能:
可实现SGD优化算法,带动量SGD优化算法,带NAG(Nesterov accelerated gradient)动量SGD优化算法,并且均可拥有weight_decay项。
参数:
params(iterable)- 参数组(参数组的概念请查看优化器基类:Optimizer),优化器要管理的那部分参数。lr(float)- 初始学习率,可按需随着训练过程不断调整学习率。momentum(float)- 动量,通常设置为0.9,0.8dampening(float)-dampening for momentum,暂时不了解其功能,在源码中是这样用的:buf.mul_(momentum).add_(1 - dampening, d_p),值得注意的是,若采用nesterov,dampening必须为 0.weight_decay(float)- 权值衰减系数,也就是L2正则项的系数。选择一个合适的权重衰减系数λ非常重要,这个需要根据具体的情况去尝试,初步尝试可以使用1e-4或者1e-3nesterov(bool)-bool选项,是否使用NAG(Nesterov accelerated gradient)
SGD+Momentum
在SGD中,gradient类比成速度(矢量),learning rate类比成时间。Momentum update(动量更新)就是我不仅要看当前时所在位置的速度向量,还要看上一步的速度(梯度),两个向量相加才是我想要的速度矢量:
# Momentum update
v = mu * v - learning_rate * dx # integrate velocity积分速度
x += v # integrate position积分位置
在这里引入了一个初始化为0的变量v和一个超参数mu。说得不恰当一点,这个变量(mu)在最优化的过程中被看做动量(一般值设为0.9),
但其物理意义与摩擦系数ρ更一致。这个变量有效地抑制了速度,降低了系统的动能,不然质点在山底永远不会停下来。通过交叉验证,这个参数通常设为[0.5,0.9,0.95,0.99]中的一个。
和学习率随着时间退火类似,Momentum随时间变化的设置有时能略微改善最优化的效果,其中动量在学习过程的后阶段会上升。一个典型的设置是刚开始将动量设为0.5而在后面的多个周期(epoch)中慢慢提升到0.99。
PyTorch中的 SGD with momentum已经在optim.SGD中的参数momentum中实现,顺便提醒一下PyTorch中的momentum实现机制和其他框架略有不同:SGD with Momentum/Nesterov
pytorch中是这样的:
v = ρ ∗ v + g v=ρ∗v+g v=ρ∗v+g
p = p − l r ∗ v = p − l r ∗ ρ ∗ v − l r ∗ g p=p−lr∗v = p - lr∗ρ∗v - lr∗g p=p−lr∗v=p−lr∗ρ∗v−lr∗g
其他框架:
v = ρ ∗ v + l r ∗ g v=ρ∗v+lr∗g v=ρ∗v+lr∗g
p = p − v = p − ρ ∗ v − l r ∗ g p=p−v = p - ρ∗v - lr∗g p=p−v=p−ρ∗v−lr∗g
ρ ρ ρ是动量, v v v是速率, g g g是梯度, p p p是参数,其实差别就是在 ρ ∗ v ρ∗v ρ∗v这一项。
Nesterov Momentum
Nesterov Momentum实际上是拿着上一步的速度先走一小步,再看当前的梯度然后再走一步。
Nesterov Momentum 与 普通Momentum 的区别:
x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v
既然我们知道动量将会把我们带到绿色箭头指向的点(x + mu * v),我们就不要在原点(红色点)那里计算梯度了。使用Nesterov动量,我们计算x + mu * v的梯度而不是“旧”位置x的梯度。
在PyTorch中,通过参数nesterov=True来实现Nesterov Momentum。
2、 torch.optim.ASGD
class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)
功能:
ASGD也称为SAG,均表示随机平均梯度下降(Averaged Stochastic Gradient Descent),简单地说ASGD就是用空间换时间的一种SGD,详细可参看论文
参数:
params(iterable)- 参数组,优化器要优化的那些参数。lr(float)- 初始学习率,可按需随着训练过程不断调整学习率。lambd(float)- 衰减项,默认值1e-4。alpha(float)- power for eta update,默认值0.75。t0(float)- point at which to start averaging,默认值1e6。weight_decay(float)- 权值衰减系数,也就是L2正则项的系数。
3、 torch.optim.Rprop
class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
功能:
实现Rprop优化方法(弹性反向传播),优化方法原文《Martin Riedmiller und Heinrich Braun: Rprop - A Fast Adaptive Learning Algorithm. Proceedings of the International Symposium on Computer and Information Science VII, 1992》
该优化方法适用于full-batch,不适用于mini-batch,因而在mini-batch大行其道的时代里,很少见到。
4、 torch.optim.Adagrad
AdaGrad、RMSProp、Adam都属于Per-parameter adaptive learning rate methods(逐参数适应学习率方法):之前的方法是对所有的参数都是一个学习率,现在对不同的参数有不同的学习率。
# Assume the gradient dx and parameter vector x
cache += dx**2
x += ‐ learning_rate * dx / (np.sqrt(cache) + eps)
注意,变量cache的尺寸和梯度矩阵的尺寸是一样的,还保持记录每个参数的梯度的平方和。
cache将用来归一化参数更新步长,归一化是逐元素进行的。注意,接收到较大梯度值的权重更新的学习率将减小,而接收到较小梯度值的权重的学习率将会变大。
有趣的是平方根的操作非常重要,如果去掉,算法的表现将会糟糕很多。用于平滑的式子eps(一般设为1e-4到1e-8之间)是防止出现除以0的情况。
Adagrad的一个缺点是:在深度学习中单调的学习率被证明通常过于激进且过早停止学习。
class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)
功能:
实现Adagrad优化方法(Adaptive Gradient),Adagrad是一种自适应优化方法,是自适应的为各个参数分配不同的学习率。这个学习率的变化,会受到梯度的大小和迭代次数的影响。梯度越大,学习率越小;梯度越小,学习率越大。缺点是训练后期,学习率过小,因为Adagrad累加之前所有的梯度平方作为分母。
详细公式请阅读:Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
John Duchi, Elad Hazan, Yoram Singer; 12(Jul):2121−2159, 2011.
5 、torch.optim.Adadelta
class torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
功能:
实现Adadelta优化方法。Adadelta是Adagrad的改进。Adadelta分母中采用距离当前时间点比较近的累计项,这可以避免在训练后期,学习率过小。
详细公式请阅读
6、 torch.optim.RMSprop
cache = decay_rate * cache + (1 ‐ decay_rate) * dx**2
x += ‐ learning_rate * dx / (np.sqrt(cache) + eps)
RMSProp简单修改了Adagrad方法,它做了一个梯度平方的滑动平均(it uses a moving average of squared gradients instead).
在上面的代码中,decay_rate是一个超参数,常用的值是[0.9,0.99,0.999]。
x+=和Adagrad中是一样的,但是cache变量是不同的。因此,RMSProp仍然是基于梯度的大小来对每个权重的学习率进行修改,这同样效果不错。但是和Adagrad不同,其更新不会让学习率单调变小。
个人觉得,RMSProp相较于Adagrad的优点是在鞍点等地方,它在鞍点呆的越久,学习率会越大。
class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
功能:
实现RMSprop优化方法(Hinton提出),RMS是均方根(root meam square)的意思。RMSprop和Adadelta一样,也是对Adagrad的一种改进。RMSprop采用均方根作为分母,可缓解Adagrad学习率下降较快的问题。并且引入均方根,可以减少摆动,详细了解可读
7 、torch.optim.Adam(AMSGrad)
Adam看起来像是RMSProp的Momentum版,简化代码如下:
m = beta1*m + (1‐beta1)*dx
v = beta2*v + (1‐beta2)*(dx**2)
x += ‐ learning_rate * m / (np.sqrt(v) + eps)
Adam看起来真的和RMSProp很像,除了使用的是平滑版的梯度m,而不是用的原始梯度向量dx。
论文中推荐的参数值eps=1e-8, beta1=0.9, beta2=0.999。
在实际操作中,我们推荐Adam作为默认的算法,一般而言跑起来比RMSProp要好一点。但是也可以试试SGD+Nesterov动量。
完整的Adam更新算法也包含了一个偏置(bias)矫正机制,因为m,v两个矩阵初始为0,在没有完全热身之前存在偏差,需要采取一些补偿措施。
class torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
功能:
实现Adam(Adaptive Moment Estimation))优化方法。Adam是一种自适应学习率的优化方法,Adam利用梯度的一阶矩估计和二阶矩估计动态的调整学习率。吴老师课上说过,Adam是结合了Momentum和RMSprop,并进行了偏差修正。
参数:
amsgrad- 是否采用AMSGrad优化方法,asmgrad优化方法是针对Adam的改进,通过添加额外的约束,使学习率始终为正值。(AMSGrad,ICLR-2018 Best-Pper之一,《On the convergence of Adam and Beyond》)。
详细了解Adam可阅读Adam: A Method for Stochastic Optimization
8 、torch.optim.Adamax
class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
功能:
实现Adamax优化方法。Adamax是对Adam增加了一个学习率上限的概念,所以也称之为Adamax。
详细了解可阅读Adam: A Method for Stochastic Optimization
9、 torch.optim.SparseAdam
class torch.optim.SparseAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08)
功能:
针对稀疏张量的一种“阉割版”Adam优化方法。
only moments that show up in the gradient get updated, and only those portions of the gradient get applied to the parameters
10、 torch.optim.LBFGS
class torch.optim.LBFGS(params, lr=1, max_iter=20, max_eval=None, tolerance_grad=1e-05, tolerance_change=1e-09, history_size=100, line_search_fn=None)
功能:
实现L-BFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化方法。L-BFGS属于拟牛顿算法。L-BFGS是对BFGS的改进,特点就是节省内存。
使用注意事项:
This optimizer doesn’t support per-parameter options and parameter groups (there can be only one).
Right now all parameters have to be on a single device. This will be improved in the future.(2018-10-07)
二、不同优化器的比较
import torch
import torch.nn.functional as F
import torch.utils.data as Data
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(1)
#hyper parameter
Learning_rate = 0.01
Batch_size = 32
Epoch =16
# fake dataset
x = torch.unsqueeze(torch.linspace(-1,1,1000),dim=1)
y = x.pow(2)+0.1*torch.normal(torch.zeros(x.size()[0], 1), torch.ones(x.size()[0], 1))
# plot dataset
plt.scatter(x.numpy(),y.numpy())
plt.show()
# 加载数据
torch_dataset = Data.TensorDataset(x,y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=Batch_size, shuffle=True)
# 为每一种优化器创建一个神经网络
class Net(torch.nn.Module):
def __init__(self):
super().__init__()
self.hidden = torch.nn.Linear(1,20)
self.predict = torch.nn.Linear(20,1)
def forward(self,x):
x = F.relu(self.hidden(x))
x = self.predict(x)
return x
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
net_Adagrad = Net()
nets = [net_SGD,net_Momentum,net_RMSprop,net_Adam,net_Adagrad]
# 创建不同的优化器用来训练不同的网络
opt_SGD = torch.optim.SGD(net_SGD.parameters(),lr=Learning_rate)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(),lr=Learning_rate,momentum=0.8,nesterov=True)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(),lr=Learning_rate,alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(),lr=Learning_rate,betas=(0.9,0.99))
opt_Adagrad = torch.optim.Adagrad(net_Adagrad.parameters(),lr=Learning_rate)
optimizers = [opt_SGD,opt_Momentum,opt_RMSprop,opt_Adam,opt_Adagrad]
criterion = torch.nn.MSELoss()
losses_his = [[],[],[],[],[]] # 记录 training 时不同神经网络的 loss
# training and plot
for epoch in range(Epoch):
for step, (b_x, b_y) in enumerate(loader):
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x)
loss = criterion(output, b_y)
opt.zero_grad()
loss.backward()
opt.step()
l_his.append(loss.data.numpy())
if step%25 == 1 and epoch%7==0:
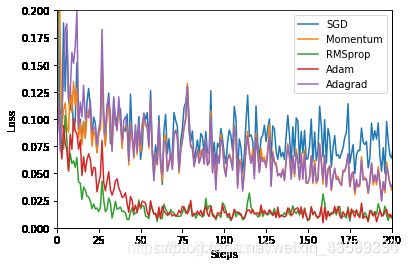
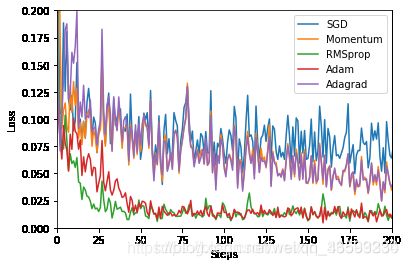
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam','Adagrad']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.xlim((0, 200))
print('epoch: {}/{},steps:{}/{}'.format(epoch+1, Epoch, step*Batch_size, len(loader.dataset)))
plt.show()
epoch: 1/16,steps:32/1000
epoch: 1/16,steps:832/1000
epoch: 8/16,steps:32/1000
epoch: 8/16,steps:832/1000
epoch: 15/16,steps:32/1000
epoch: 15/16,steps:832/1000
一个有趣的现象是Adagrad和Momentum走势非常相似,有空可以思考一下。
三、直观看不同优化方法的动态学习过程
图片版权: Alec Radford
第一张图是损失函数的等高线:
第二张图是在鞍点处的学习情况,注意SGD很难突破对称性,一直卡在顶部。而RMSProp之类的方法能够看到马鞍方向有很低的梯度。因为在RMSProp更新方法中的分母项,算法提高了在该方向的有效学习率,使得RMSProp能够继续前进:
参考博客:
https://blog.csdn.net/qq_36589234/article/details/89330342?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param
https://blog.csdn.net/u011995719/article/details/88988420