PTA|浙大版《C语言程序设计实验与习题指导（第3版）》实验3-1 求一元二次方程的根 (20分)

题目

本题目要求一元二次方程的根，结果保留2位小数。

输入格式:
输入在一行中给出3个浮点系数a、b、c，中间用空格分开。

输出格式:
根据系数情况，输出不同结果：

1)如果方程有两个不相等的实数根，则每行输出一个根，先大后小；

2)如果方程有两个不相等复数根，则每行按照格式“实部+虚部i”输出一个根，先输出虚部为正的，后输出虚部为负的；

3)如果方程只有一个根，则直接输出此根；

4)如果系数都为0，则输出"Zero Equation"；

5)如果a和b为0，c不为0，则输出"Not An Equation"。

输入样例1:

2.1 8.9 3.5

输出样例1:

-0.44
-3.80

输入样例2:

1 2 3

输出样例2:

-1.00+1.41i
-1.00-1.41i

输入样例3:

0 2 4

输出样例3:

-2.00

输入样例4:

0 0 0

输出样例4:

Zero Equation

输入样例5:

0 0 1

输出样例5:

Not An Equation

参考解答（AC代码）

#include
#include
int main(){
    double a,b,c,delta,real1,real2,imag1=0,imag2=0;
    scanf("%lf %lf %lf",&a,&b,&c);
    delta=b*b-4*a*c;
    //判断方程是否可解
    if(a==0&&b==0&&c==0){
    	printf("Zero Equation");
	}
	else if(a==0&&b==0&&c!=0){
		printf("Not An Equation");
	}
    else{
    	//对可解方程运算
	    if(a!=0){
	    	 if(delta>=0){
	    		real1=(-b+sqrt(delta))/(2*a);
	    		real2=(-b-sqrt(delta))/(2*a);
			}
			else{
				real1=real2=(b==0)?0:(-b)/(2*a);
				imag1=sqrt(-delta)/(2*a);
				imag2=-imag1;
			}
		}
		else{
			real1=real2=-c/b;			
		}
		//输出
		if(imag1==0){
			printf("%.2lf",real1);
			if(real1!=real2)printf("\n%.2lf",real2);
		}
		else{
//			if(real1==0){
//				printf("%.2lfi\n%.2lfi",imag1,imag2);
//			}
//			else{
				printf("%.2lf%+.2lfi\n",real1,imag1);
				printf("%.2lf%+.2lfi",real2,imag2);				
//			}
		}
	}	
    return 0;
}

测试点细节

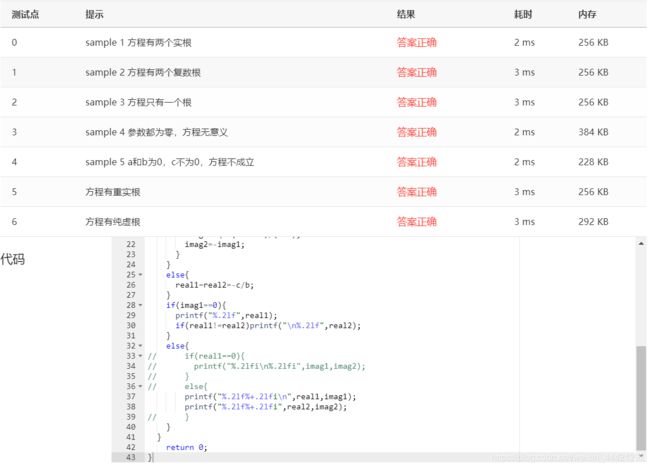
第一次提交，根据一元二次方程的判别式和a，b，c的零值情况，用平级的if-else结构来输出不同情况的解。结果是，不同的情况太多了！还出现了 x+0i 的情况。索性放弃了分情况输出，改成先分情况对有效方程进行运算，用real1，real2，imag1，imag2来分别存x1的实部、x2的实部，x1的虚部，x2的虚部，最后按四个变量的值来分情况输出。

值得注意的是：

1、即使实部为零，依然需要输出“实部+虚部i”的格式，即“0.00+bi”。因为统一输出结果，我先是判断了实部、虚部是否为零，如果为零则放弃输出。提交后纯虚数总是过不了，后来重新审题，发现条件二中说明当解为复数时，必须按“实部+虚部i”的格式输出。果然将判断实部是否为零的语句注释掉，就通过了。
2、在求根的实部时，公式(-b)/(2a)最好写成(b==0)?0:(-b)/(2a)。因为当b=0时，结果会是-0。
3、在输出“实部+虚部i”格式时，可以利用格式控制符%+在虚部为正时输出“+”号。