R语言学习记录:主成分分析的R实现
时间: 2018-08-09
教程:知乎:Learn R | 数据降维之主成分分析(上)、Learn R | 数据降维之主成分分析(下) 作者:Jason
数据来源:《应用多元统计分析》 王学民 编著 P228-P230 习题7.6、7.7
主成分分析
1.主成分分析
使用psych包对数据进行主成分分析。
其中,principal函数进行主成分分析,fa.parallel函数生成碎石图。
principal(r, nfactors = 1, residuals = FALSE, rotate = “varimax”,
n.obs = NA, covar = FALSE, scores = TRUE,missing = FALSE, impute =
“median”, oblique.scores=TRUE, method = “regression”,…)
r:指定输入的数据,如果输入的是原始数据,R将自动计算其相关系数矩阵 nfactors:指定主成分个数
residuals:是否显示主成分模型的残差,默认不显示 rotate:指定模型旋转的方法,默认为最大方差法
n.obs:如果输入的数据是相关系数矩阵,则必须指定观测样本量
covar:逻辑参数,如果输入数据为原始数据或方阵(如协方差阵),R将其转为相关系数矩阵 scores:是否计算主成分得分
missing:缺失值处理方式,如果scores为TRUE,且missing也为TRUE,缺失值将被中位数或均值替代
impute:指定缺失值的替代方式,默认为中位数替代; method:指定主成分得分的计算方法,默认使用回归方法计算。
(摘自教程)
如:
导入数据:
> library(openxlsx)
> data1 <- read.xlsx("E:\\Learning_R\\主成分分析\\exec7.6.xlsx", rowNames = TRUE, rows = 1:51, cols = 1:8)
> head(data1)
杀人罪 强奸罪 抢劫罪 伤害罪 夜盗罪 盗窃罪 汽车犯罪
Alabama 14.2 25 97 278 1136 1882 281
Alaska 10.8 52 97 284 1332 3370 753
Arizona 9.5 34 138 312 2346 4467 440
Arkansas 8.8 28 83 203 973 1862 183
California 11.5 49 287 358 2139 3500 664
Colorado 6.3 42 171 293 1935 3903 477生成碎石图:
> library(psych)
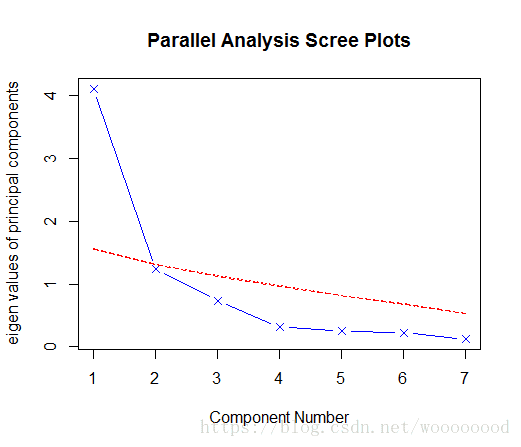
> fa.parallel(data1, fa = 'pc', n.iter = 100, show.legend = FALSE)
Parallel analysis suggests that the number of factors = NA and the number of components = 1 主成分分析:
> data1_pca <- principal(data1, nfactors = 2, rotate = "none")
> data1_pca
Principal Components Analysis
Call: principal(r = data1, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 h2 u2 com
杀人罪 0.61 -0.70 0.86 0.14 2.0
强奸罪 0.88 -0.19 0.80 0.20 1.1
抢劫罪 0.81 0.05 0.65 0.35 1.0
伤害罪 0.80 -0.38 0.79 0.21 1.4
夜盗罪 0.89 0.23 0.85 0.15 1.1
盗窃罪 0.72 0.45 0.73 0.27 1.7
汽车犯罪 0.60 0.56 0.67 0.33 2.0
PC1 PC2
SS loadings 4.11 1.24
Proportion Var 0.59 0.18
Cumulative Var 0.59 0.76
Proportion Explained 0.77 0.23
Cumulative Proportion 0.77 1.00
Mean item complexity = 1.5
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.09
with the empirical chi square 16 with prob < 0.036
Fit based upon off diagonal values = 0.97principal函数中,第一个参数是数据,第二个参数说明要保留两个主成分,第三个参数为旋转方法,为”none”,即不进行主成分旋转。
输出结果中,第一部分中PC1和PC2为两个主成分在各观测变量上的载荷,即观测变量与主成分的相关系数。h2是主成分公因子方差,即主成分对每个变量的方差解释度;u2是成分唯一性,即方差无法被主成分解释的比例,u2+h2=1。第二部分是对于两个主成分的说明,SS loadings行是两主成分的特征值,Proportion Var是方差比例,即各主成分对数据的解释程度,Cumulative Var是累计方差比例。
主成分旋转:
> data1_pca_xz <- principal(data1, nfactors = 2, rotate = "varimax")
> data1_pca_xz
Principal Components Analysis
Call: principal(r = data1, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 h2 u2 com
杀人罪 -0.05 0.93 0.86 0.14 1.0
强奸罪 0.50 0.74 0.80 0.20 1.8
抢劫罪 0.61 0.52 0.65 0.35 2.0
伤害罪 0.32 0.83 0.79 0.21 1.3
夜盗罪 0.80 0.46 0.85 0.15 1.6
盗窃罪 0.83 0.18 0.73 0.27 1.1
汽车犯罪 0.82 0.01 0.67 0.33 1.0
RC1 RC2
SS loadings 2.74 2.62
Proportion Var 0.39 0.37
Cumulative Var 0.39 0.76
Proportion Explained 0.51 0.49
Cumulative Proportion 0.51 1.00
Mean item complexity = 1.4
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.09
with the empirical chi square 16 with prob < 0.036
Fit based upon off diagonal values = 0.97> head(data1_pca_xz$weights)
RC1 RC2
杀人罪 -0.285 0.510
强奸罪 0.048 0.257
抢劫罪 0.167 0.108
伤害罪 -0.073 0.358
夜盗罪 0.283 0.018
盗窃罪 0.377 -0.139rotate = varimax表示旋转方式为正交因子旋转。
由输出结果可以看出,两个主成分的方差比例不变,但在各观测值上的载荷发生了改变,一般情况下,进行因子旋转是为了更好的解释主成分。
data1_pca_xz$weights的内容为主成分与原始变量之间之间线性回归方程的系数。
principal函数中主成分得分默认不进行计算,在函数中将scores参数的值改为TRUE即可计算主成分得分。计算主成分得分:
> data1_pca_xz1 <- principal(data1, nfactors = 2, rotate = "varimax", scores = TRUE)
> options(digits = 2) # 显示两位小数
> head(data1_pca_xz1$scores)
RC1 RC2
Alabama -1.32 1.34
Alaska 0.96 0.72
Arizona 1.60 0.48
Arkansas -1.21 0.51
California 1.61 1.37
Colorado 1.46 0.26生成主成分分析图:
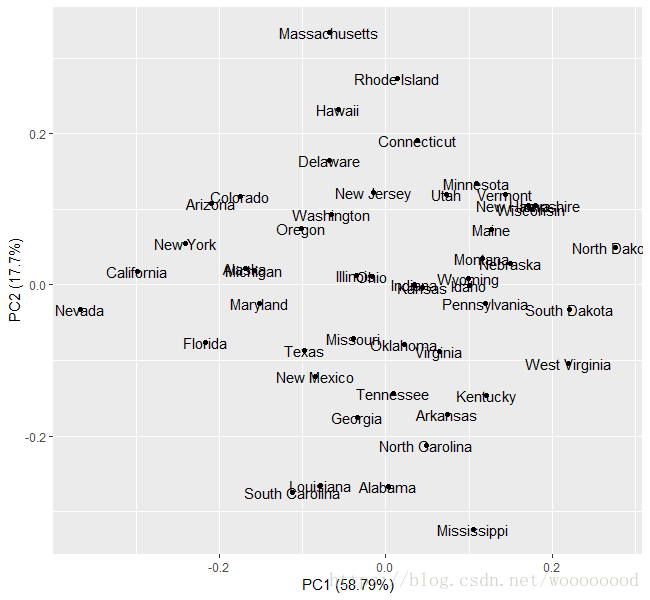
> autoplot(prcomp(data1, scale = TRUE), label = TRUE)2.练习
练习内容:《应用多元统计分析》 王学民 编著 P230 习题7.7
数据内容为纽约股票交易所的五只股票(阿莱德化学、杜邦、联合碳化物、埃克森和德士古)从1975年1月到1976年12月期间的周回报率。
阿莱德化学、杜邦和联合碳化物属于化工类股票,埃克森和德士古属于石油类股票。
> library(openxlsx)
> data2 <- read.xlsx("E:\\Learning_R\\主成分分析\\exec7.7.xlsx", rows = 1:101, cols = 1:5)
> head(data2)
阿莱德化学 杜邦 联合碳化物 埃克森 德士古
1 0.0000 0.0000 0.000 0.039 0.000
2 0.0270 -0.0449 -0.003 -0.014 0.043
3 0.1228 0.0608 0.088 0.086 0.078
4 0.0570 0.0299 0.067 0.014 0.020
5 0.0637 -0.0038 -0.040 -0.019 -0.024
6 0.0035 0.0508 0.083 0.074 0.050
> library(psych)
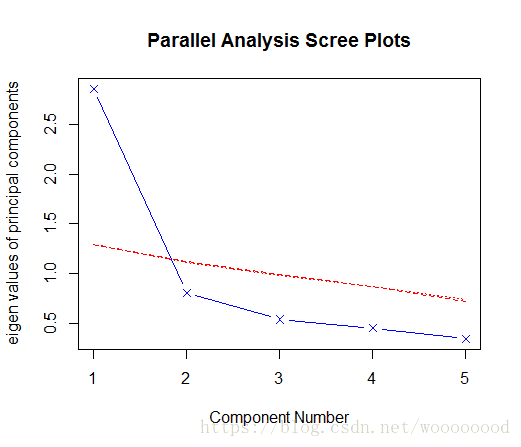
> fa.parallel(data2, fa = 'pc', n.iter = 100, show.legend = FALSE)
Parallel analysis suggests that the number of factors = NA and the number of components = 1 > data2_pca1 <- principal(data2, nfactors = 2, rotate = "none")
> data2_pca1
Principal Components Analysis
Call: principal(r = data2, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 h2 u2 com
阿莱德化学 0.78 -0.22 0.66 0.34 1.2
杜邦 0.77 -0.46 0.81 0.19 1.6
联合碳化物 0.79 -0.23 0.69 0.31 1.2
埃克森 0.71 0.47 0.73 0.27 1.7
德士古 0.71 0.52 0.78 0.22 1.8
PC1 PC2
SS loadings 2.86 0.81
Proportion Var 0.57 0.16
Cumulative Var 0.57 0.73
Proportion Explained 0.78 0.22
Cumulative Proportion 0.78 1.00
Mean item complexity = 1.5
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.11
with the empirical chi square 24 with prob < 8.8e-07
Fit based upon off diagonal values = 0.95由输出结果可知,第一主成分在5个观测变量上的载荷均较大,第二主成分在杜邦、埃克森和德士古这三个变量上载荷较大,在阿莱德化学和联合碳化物上载荷相对较小,但相差不大。两主成分解释了该数据的73%,但该结果并不便于解释两主成分。因此,考虑进行主成分旋转。
> data2_pca2 <- principal(data2, nfactors = 2, rotate = "varimax")
> data2_pca2
Principal Components Analysis
Call: principal(r = data2, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
RC1 RC2 h2 u2 com
阿莱德化学 0.75 0.32 0.66 0.34 1.4
杜邦 0.89 0.12 0.81 0.19 1.0
联合碳化物 0.77 0.31 0.69 0.31 1.3
埃克森 0.26 0.81 0.73 0.27 1.2
德士古 0.23 0.85 0.78 0.22 1.1
RC1 RC2
SS loadings 2.06 1.61
Proportion Var 0.41 0.32
Cumulative Var 0.41 0.73
Proportion Explained 0.56 0.44
Cumulative Proportion 0.56 1.00
Mean item complexity = 1.2
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is 0.11
with the empirical chi square 24 with prob < 8.8e-07
Fit based upon off diagonal values = 0.95
> autoplot(prcomp(data2, scale = TRUE), label = TRUE)
由输出结果可知,第一主成分在阿莱德化学、杜邦和联合碳化物这三个变量上载荷较大较大,因此,第一主成分可以解释为化工类股票的回报率。第二主成分埃克森和德士古这两个变量上载荷较大,因此,第二主成分可以解释为石油类股票的回报率。
(主成分分析图的解释略)