线性判别分析(LDA)和python实现（多分类问题）

上一篇写过线性判别分析处理二分类问题https://blog.csdn.net/z962013489/article/details/79871789，当使用LDA处理多分类问题时，通常是作为一个降维工具来使用的。若我们有一个D维的样本集，该样本集包含C个类别共n个样本，希望将D维降维成K维。之前在二分类问题中，我们定义的类间散度矩阵为：

Sb=(μ1−μ2)(μ1−μ2)T S b = ( μ 1 − μ 2 ) ( μ 1 − μ 2 ) T

当类别为3时就已经不再适用，在这里引出全局散度矩阵的概念：

St=Sw+Sb=∑i=1n(xi−μ)(xi−μ)T S t = S w + S b = ∑ i = 1 n ( x i − μ ) ( x i − μ ) T

其中 μ μ 为整个样本集的均值向量，其中的类内散度矩阵 Sw S w 定义为所有类别的散度矩阵之和，与二分类类似，基于全局散度矩阵，我们就可以求得类间散度矩阵 Sb S b 定义为：

Sb=St−Sw=∑i=1nmi(μi−μ)(μi−μ)T S b = S t − S w = ∑ i = 1 n m i ( μ i − μ ) ( μ i − μ ) T

其中 mi m i 为第i个类别样本总数， μi μ i 为第i个类别样本的均值向量。

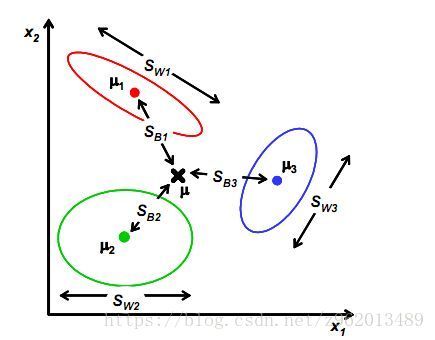
上图的例子可以作为参考便于理解。
我们要计算一个W矩阵，使样本向量在该投影矩阵的作用下能够实现其与同类样本的中心距离尽量小，而与异类样本的中心距离尽量大。常见的一种优化目标为：

maxWtr(WTSbW)tr(WTSwW) max W t r ( W T S b W ) t r ( W T S w W )

其中的tr()为矩阵的迹，一个n×n的对角矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)。
这个优化目标实际上等价于求解多个w组合成W，那么该问题就等价于求解多个上一章的优化目标，使用相同的方法，可以求得下式：

SbW=λSwW S b W = λ S w W

即

S−1wSbW=λW S w − 1 S b W = λ W

W的闭式解为 S−1wSb S w − 1 S b 的k个最大非零广义特征值对应的特征向量组成的矩阵，LDA降维最多可以降至C-1，C为样本类别数，与原始特征维数n无关。
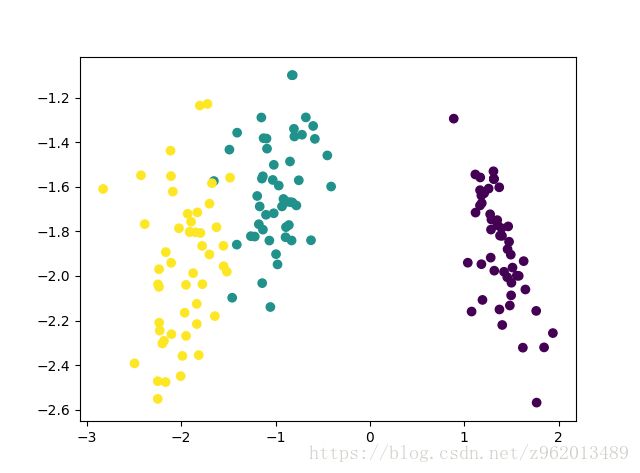
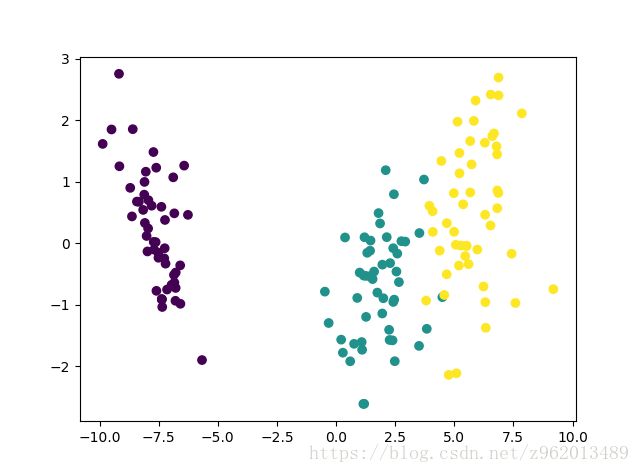
使用python实现LDA降维代码，对Iris数据集从四维降至二维，绘图如下：
其中上图为自己实现的方法降维表现，下图为sklearn自带方法降维表现。

python3.6实现如下：

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis


def LDA_dimensionality(X, y, k):
    '''
    X为数据集，y为label，k为目标维数
    '''
    label_ = list(set(y))

    X_classify = {}

    for label in label_:
        X1 = np.array([X[i] for i in range(len(X)) if y[i] == label])
        X_classify[label] = X1

    mju = np.mean(X, axis=0)
    mju_classify = {}

    for label in label_:
        mju1 = np.mean(X_classify[label], axis=0)
        mju_classify[label] = mju1

    #St = np.dot((X - mju).T, X - mju)

    Sw = np.zeros((len(mju), len(mju)))  # 计算类内散度矩阵
    for i in label_:
        Sw += np.dot((X_classify[i] - mju_classify[i]).T,
                     X_classify[i] - mju_classify[i])

    # Sb=St-Sw

    Sb = np.zeros((len(mju), len(mju)))  # 计算类内散度矩阵
    for i in label_:
        Sb += len(X_classify[i]) * np.dot((mju_classify[i] - mju).reshape(
            (len(mju), 1)), (mju_classify[i] - mju).reshape((1, len(mju))))

    eig_vals, eig_vecs = np.linalg.eig(
        np.linalg.inv(Sw).dot(Sb))  # 计算Sw-1*Sb的特征值和特征矩阵

    sorted_indices = np.argsort(eig_vals)
    topk_eig_vecs = eig_vecs[:, sorted_indices[:-k - 1:-1]]  # 提取前k个特征向量
    return topk_eig_vecs


if '__main__' == __name__:

    iris = load_iris()
    X = iris.data
    y = iris.target

    W = LDA_dimensionality(X, y, 2)
    X_new = np.dot((X), W)
    plt.figure(1)
    plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)

    # 与sklearn中的LDA函数对比
    lda = LinearDiscriminantAnalysis(n_components=2)
    lda.fit(X, y)
    X_new = lda.transform(X)
    print(X_new)
    plt.figure(2)
    plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)

    plt.show()