记忆化搜索专题

文章例题
HDU–1078–FatMouse and Cheese–
HDU–1978–How many ways–

什么是记忆化搜索呢？

搜索的低效在于没有能够很好地处理重叠子问题；
动态规划虽然比较好地处理了重叠子问题，但是在有些拓扑关系比较复杂的题目面前，又显得无奈。记忆化搜索正是在这样的情况下产生的，它采用搜索的形式和动态规划中递推的思想将这两种方法有机地综合在一起，扬长避短，简单实用，在信息学中有着重要的作用。
　　用一个公式简单地说：记忆化搜索=搜索的形式+动态规划的思想。

记忆化搜索的思想

记忆化搜索的思想是,在搜索过程中，会有很多重复计算,如果我们能记录一些状态的答案，就可以减少重复搜索量

记忆化搜索的适用范围

根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关”的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。
也就是说，他的问题表达，不是单纯生成一个走步方案，而是生成一个走步方案的代价等，而且每走一步，在搜索树/图中生成一个新状态，都可以精确计算出到此为止的费用，也就是，可以分步计算，这样才可以套用已经得到的答案

记忆化搜索的核心实现

a. 首先，要通过一个表记录已经存储下的搜索结果，一般用哈希表实现
b.状态表示，由于是要用哈希表实现，所以状态最好可以用数字表示，常用的方法是把一个状态连写成一个p进制数字，然后把这个数字对应的十进制数字作为状态
c.在每一状态搜索的开始，高效的使用哈希表搜索这个状态是否出现过，如果已经做过，直接调用答案，回溯
d.如果没有，则按正常方法搜索
记忆化搜索是类似于动态规划的，不同的是，它是倒做的“递归式动态规划”。

HDU–1078–FatMouse and Cheese–



**题目大意：**老鼠可以横着竖着走1-k步，下一步走的必须比现在的奶酪多

#include 
using namespace std;
int maze[1100][1100];
int n,m;
int ans;
int dp[1100][1100];
int dfs(int x,int y)
{
    if(dp[x][y]){
        return dp[x][y];
    }
    int sum=0;//注意sum一定不能是全局的，因为递归时会有更改，害我WA了好多次
    for(int i=max(x-m,0);i<min(x+m+1,n);i++){
        if(maze[i][y]>maze[x][y])
        sum=max(sum,dfs(i,y));
    }
    for(int i=max(y-m,0);i<min(y+m+1,n);i++){
        if(maze[x][i]>maze[x][y])
        sum=max(sum,dfs(x,i));
    }
    dp[x][y]=maze[x][y]+sum;
    return dp[x][y];
}
int main()
{
    while(cin>>n>>m && (n!=-1 || m!=-1)){
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                cin>>maze[i][j];
            }
        }
        memset(dp,0,sizeof(dp));
        dfs(0,0);
        cout<<dp[0][0]<<endl;
    }
    return 0;
}

HDU–1978–How many ways–


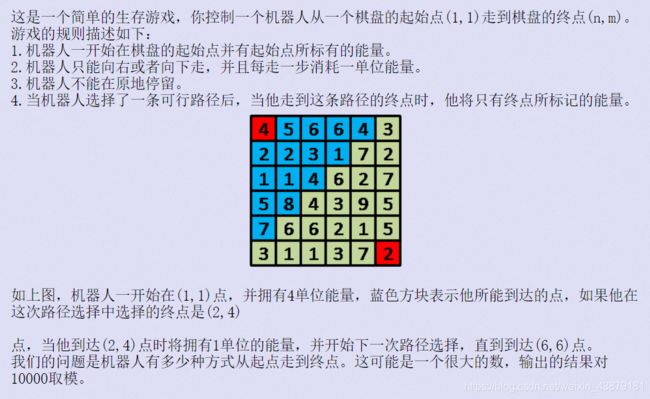
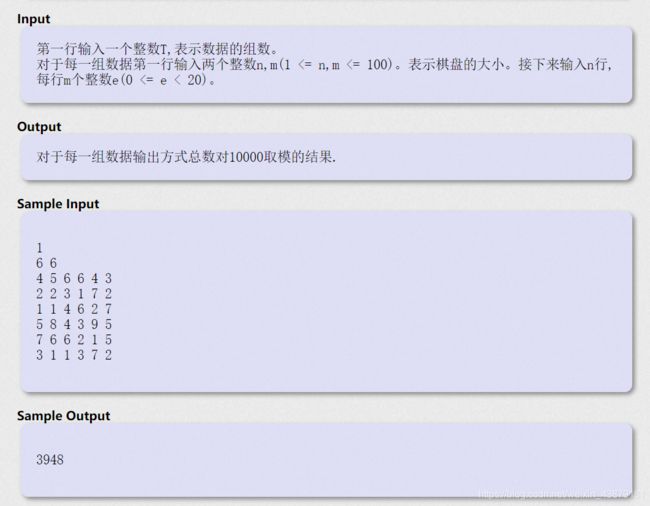
题目思路：
dp【i】【j】这里表示从【i】【j】到【n】【m】有多少条路。那么dp【n】【m】表示【n】【m】到【n】【m】有多少条路；当然是1条，既dp【n】【m】=1这是已知的；那么【n】【m-1】；到【n】【m】有多少条路呢；他们距离只有一步所以是一条。所以dp【n】【m-1】=1；那么dp【n-1】【m】也等于1了；

#include 
using namespace std;
const int N=10000;
int a[107][107];
int dp[107][107];
int t,m,n;
bool check(int x,int y) {
	if(x<1||x>m||y<1||y>n)return true;
	else return false;
}
int solve(int x,int y) {
	if(dp[x][y]>=0)return dp[x][y];
	dp[x][y]=0;
	for(int i=0; i<=a[x][y]; i++) {
		for(int j=0; j<=a[x][y]-i; j++) {//遍历所有可能
			if(check(x+i,y+j))continue;
			dp[x][y]=(dp[x][y]+solve(x+i,y+j))%N;
		}
	}
	return dp[x][y];
}
int main() {
	cin>>t;
	while(t--) {
		cin>>m>>n;
		for(int i=1; i<=m; i++) {
			for(int j=1; j<=n; j++) {
				cin>>a[i][j];
			}
		}
		memset(dp,-1,sizeof(dp));
		dp[m][n]=1;
		cout<<solve(1,1)%N<<endl;
	}
	return 0;
}