代码随想录+力扣刷题记录+华为机考准备记录
为了准备华为机考的刷题记录,已压线过
背景:数据结构与算法零基础,此前没有刷过题,会Python。
学习路线
- 按照代码随想录的顺序刷题,刷题平台:力扣
- 以上大致过了一遍后开始刷华为机考真题(cdsn上购买的真题,刷题平台是购买的真题中的OJ平台,也是ACM模式)
- 总共用时1个月。完成情况:力扣80个题+华为2024年机考真题。大部分题目都只做过1次,掌握得很不牢固,机考的时候也是压线过。
- 时间比较紧急,做到后期缺少总结消化,也没有时间记录,所以这篇笔记很不全面,等秋招刷题再进一步补充。
代码随想录内容
数组
主要方法有二分查找、双指针法、滑动窗口、模拟行为,这四个分类是按照代码随想录分的。
二分查找
1. 注意区间的开闭,坚持循环不变量原则
2. middle的定义:mid = left +(right-left)//2,注意要把左边的索引加上
双指针法
- 快慢指针:力扣 27. 移除元素:数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。快指针:找到新数组,即不等于val的值,慢指针:指向更新 新数组下标的位置
- 相向指针:力扣 977.有序数组的平方 借鉴思路:从两端向中间搜索
- 三(多)个指针:力扣 15. 三数之和 力扣 18. 四数之和
力扣 15. 三数之和
为什么可以用双指针?因为题目是返回值,而不是索引,所以可以对数组排序,利用排序后的规律去移动指针(可以对比两数之和为什么不能直接用双指针,因为两数之和需要返回索引)
三个指针:i +left+right,先对数组排序,然后固定i,left=i+1,right=len(nums)-1,判断三数之和与0的关系,大于0,则right左移,小于0,则left右移
为什么不能像两数之和、四数相加Ⅱ用哈希表解决?因为这里要求返回的数组不重复,用哈希表做的话,去重逻辑很复杂。这里用指针法遍历,遇到重复的元素,continue即可
力扣 18. 四数之和
与三数之和类似,只不过再套一层for循环,也可以理解成再加一个指针(i+j+left+right),先固定i,j,left=j+1,right=len(nums)-1
滑动窗口
力扣 209.长度最小的子数组
注意在这种题里,数组元素都是正的。跟前缀和做比较(力扣560.和为K的子数组)
模拟行为
力扣 59.螺旋矩阵Ⅱ
坚持循环不变量原则
难点:抽象出一个重复进行的过程
哈希表
用来快速判断一个元素是否出现集合里
python常见的三种哈希结构:列表、集合、字典
字母问题
- 力扣 242.有效的字母异位词
- 力扣 49.字母异位词分组
- 力扣 383. 赎金信
判断异位词的方法:
- 用record记录字母的相对ASCII码,判断两个单词的record是否相同(或者是遍历第一个单词record[i]+1,遍历第二个单词record[i]-1,检查最后record是否为0 )
- 将字符串转换为列表,再排序,因为字母是有序的,可以进行排序,排序后再看两个字母列表是否相同
- 用Counter,可以直接返回字符串的统计结果
from collections import Counter集合问题
集合中的元素不可重复,所以可以用来判断元素是否重复出现,输出不含有重复元素的结果
力扣 349. 两个数组的交集
交集中不含有重复元素,可以用集合解决
set() & set()
力扣 202. 快乐数
如果陷入死循环,说明该数不是快乐数,如何判断陷入循环?判断结果是否重复出现过,所以用集合存储结果
和问题
共同点:创建一个哈希表,遍历元素时,查找目标和-当前元素是否存在与该表中,如果存在,说明找到了目标元素,如果不存在,则将该元素记录进哈希表中,方便后续查找
- 力扣 1 两数之和
- 力扣 454.四数相加Ⅱ
- 力扣 560.和为K的子数组(前缀和)
力扣 454.四数相加II:先遍历前两个数组的元素,用字典统计a+b的和出现的次数,再遍历后两个数组,如果target-(c+d)在字典中出现过,则count+1
其中 和为K的子数组,是存储每个数字对应的前缀和s[j](和不包括自身),并查找s[j]-k是否在字典中,如果在,说明存在一个子数组和为k
其他类型:存储长度...
力扣 128 最长连续序列
最长连续序列,是存储每个数字当前的最长长度,并查找num-1和num+1是否在字典中,如果存在,则需要加上前后的长度,并更新边界元素的长度
字符串
反转问题
- 双指针,left+right,交换两个字母
- 利用栈
- 切片[::-1]
- reverse/reversed
- range函数,for i in range(n,-1,-1)
栈与队列
二叉树
二叉树的递归遍历
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
Tips:按照中节点记忆,“左”和“右”指的是子树,不是节点
Leetcode144,145,94
二叉树的迭代遍历
使用栈模拟迭代过程
前序遍历思路:stack=[root]。递归过程:pop,记录;右孩子入栈,左孩子入栈,直到栈为空
前序和后序的代码调整一下顺序+翻转即可
中序的节点访问和节点处理是分开的,需要用指针记录访问过的节点
cur = root,指针一路向左,把左节点放进栈,直到叶结点(左孩子为空),else:pop,记录(node.val,因为是左中右),访问右孩子,cur = node.right
Leetcode144,145,94
回溯算法
解决什么问题
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
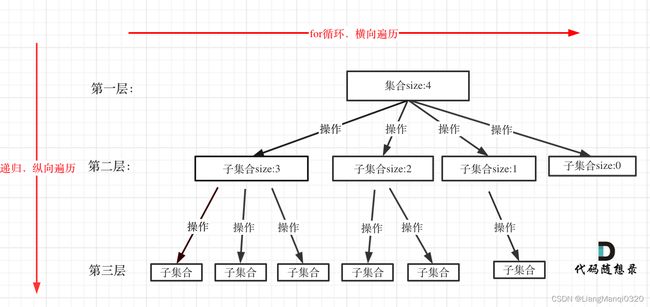
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
组合问题+优化
思路:
1.定义函数功能
backtracking:从组合中依次抽出一个数,把这个数添加到结果中,然后弹出
2.寻找递归终止条件
结果长度==k
3.递推函数的等价关系式
backtracking = 从组合中依次抽出一个数,把这个数添加到结果中,剩下的组合backtracking,然后弹出
优化:剪枝,修改终止节点的索引
需要startIndex来控制for循环的起始位置
组合总和Ⅲ
剪枝:除了结束索引可以优化,还可以判断和是否大于目标值
回溯:节点处理除了添加进path,还需要对和进行回溯
电话号码的字母组合
不会的点:建立电话号码与字母的映射(二维列表就能解决),字符串的回溯(不是用pop,应该是切片[:-1]),index是指的数字集合,而不是字母集合
组合总和
这里元素可以重复选取,因此statrIndex不是i+1了,而是i,其他部分与组合总和Ⅲ相同
组合总和Ⅱ
这里给定的元素集合是有重复元素的,而结果集不能重复,因此需要去重
去重逻辑:树层去重和树枝去重,需要先对元素排序,在循环过程中遇到重复的元素,则跳过搜索过程,为了做到树层去重而不是树枝去重,需要i>startIndex and candidates[i]==candidates[i-1]
在求和问题中,排序之后加剪枝是常见的套路!
分割回文串
切割问题,切割线用代码如何表示?startIndex控制。如何判断回文串?s==s[::-1]
复原IP地址
同样是切割问题,需要控制树的深度,判断字符串是否有效,返回的格式
子集
在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
子集问题可以不写终止条件
子集Ⅱ
与组合去重问题相同
非递减子序列
去重:不能排序后再去重,所以需要用一个set或者数组存放同一层中已经遍历过的元素,每层遍历时,判断该元素是否已经遍历过了
全排列
不用startIndex控制元素的不重复,因为排列跟元素顺序也有关
使用used数组记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次
全排列Ⅱ
当所给元素有重复值的时候,如果不能对原数组排序,则用set去重,如果可以排序,则使用used数组去重,使用used数组的时候,需要注意有一个条件是used[i-1] == False,决定是树枝去重还是树层去重
N皇后(pass)
遍历每一行,在每一列放皇后,需要判断放的位置是否合法
有时间再二刷
解数独(pass)
二维递归
超时,有时间看用集合如何处理
动态规划
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
斐波那契数
爬楼梯
花费最小力气爬楼梯
学会递归的思路,一个一个变量开始推导,发现规律
不同路径
当前点只能从哪里来
63.不同路径Ⅱ
难点:第一行第一列如何初始化?首先初始化为0,遍历第一行第一列,没遇到障碍物就设定为1,遇到障碍物直接break,后面就都为0了
循环时遇到障碍物continue,因为遇到障碍物的时候,证明无法到达该点,即该点的路径为0
343.整数拆分
难点:dp[i]从什么状态推导而来?有两种方案:dp[i-j]*j, (i-j)*j
遍历可能的拆分方案:j从1到 i//2,dp[i]=max(dp[i], dp[i-j]*j, (i-j)*j),记得与上一次的dp[i]作比较
背包问题
0-1背包
物品有限
二维dp数组:dp[i][j] 表示在0-i物品中任取,容量为 j 的背包能装的最大价值,遍历顺序无限制
滚动一维dp数组:dp[j] 表示容量为 j 的背包能装的最大价值,需要先遍历物品,再遍历背包,且背包要倒序遍历,否则物品会被重复放进去
416.分割等和子集
最后一块石头的重量Ⅱ
494.目标和
打家劫舍问题
环形转换为线性
不同的二叉搜索树、打家劫舍Ⅲ与二叉树相关,先不做
股票问题
子序列问题
图论
DFS:递归,搜索一个节点,递归搜索该节点的子节点,直到搜到终点,再回退
BFS:队列存放该层所有节点,依次取出,再取每一层的所有节点
Dijkstra算法
class Dijkstra(object):
def __init__(self, graph, start, goal):
# 邻接表,双层字典,{节点:{连接的节点:}距离}
self.graph = graph
# 一共有n个节点
n = len(graph)
# 起点
self.start = start
self.goal = goal
# 定义一个存放起点到当前节点的最短距离的字典
self.distance = {}
# 定义一个存放父节点的数组,一开始为空,都没有父节点
self.father = {}
# 定义一个优先队列,可以存放遍历到的节点及起点到该节点的值
self.queue = {}
self.queue[start] = 0
# 记录最短路径
self.minDis = 0
def searchPath(self):
while True:
# 如果队列为空,说明没有找到起点到终点的路径
if not self.queue:
print('搜索失败')
return -1
# 找到队列里距离最小的节点,将其弹出做处理
minDistance, minNode = min(zip(self.queue.values(), self.queue.keys()))
self.queue.pop(minNode)
# 更新距离表的该节点的值,
self.distance[minNode] = minDistance
# 如果当前节点已经是终点,则不需要继续搜索了,返回最短路径
if minNode == self.goal:
self.minDis = minDistance
path = [self.goal]
father_node = self.father[self.goal]
# 回溯找到路径,当父节点为起点时,说明找到了一条完整的路径,可以返回结果了
while father_node != self.start:
path.append(father_node)
father_node = self.father[father_node]
path.append(self.start)
print('最短路径为:',path[::-1])
print('最短路径长度为:',self.minDis)
return path[::-1],self.minDis
path.append()
# 找到该节点下面的节点,将其添加到queue中
for node in self.graph[minNode].keys():
# 如果该节点已经处理过了,则无需重复添加
if node in self.distance:
continue
# 计算现在的距离
curDis = self.graph[minNode][node] + minDistance
# 如果节点已经在queue中,则比较两者的距离大小,如果现在的距离小于queue中记录的这个点的距离,则将距离修改为小的距离
if node in self.queue:
if self.queue[node] > curDis:
self.queue[node] = curDis
# 相应的,修改node的父节点,改为minNode
self.father[node] = minNode
# 如果节点不queue中,则直接添加
else:
self.queue[node] = curDis
# 相应的,修改node的父节点,改为minNode
self.father[node] = minNode
做题遇到的语法点
self的用法
Python中self用法详解_python self-CSDN博客
递归
- 第一步,定义函数功能
- 第二步,寻找递归终止条件
- 第三步,递推函数的等价关系式:原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式,这个步骤就等价于寻找原问题与子问题的关系,如何用一个公式把这个函数表达清楚
递归详解-CSDN博客
递归详解——让你真正明白递归的含义-CSDN博客
list[] 和 list[:] 的理解
list“赋值”时会用到list2 = list1 或者 list2[:] = list1,前者两个名字指向同一个对象,后者两个名字指向不同对象。理解如下:
首先,python中没有赋值的说法,只有名称到对象的引用;
list2 = list1是把list1所指的对象绑定到名字list2上,没有产生新list,只是新增了一个引用;
正因为两个名称指向的同一个对象,所以修改list1,那么list2也会改变;
通俗理解:以前有一套三室一厅的房子,户主叫list1。后来list1和list2结婚,房产证上户主的名字加了一个,但房子还是只有一套。list1如果把客厅刷成了蓝色,那list2回家的时候会发现客厅是蓝色的了。
而list2 = list1[:]则是把list1通过切片运算取得的新list对象绑定到list2上,产生了新list,名称和引用也不同,所以,修改其中一个,另一个不会变。
题目:Leetcode 77组合,到底是append(path),还是append(path[:])
while 语句
执行语句可以是单个语句或语句块,判断形式可以是任何表达式,任何非零或非空的表达式皆为True,当判断条件为False时,循环结束。
判断条件是常值,表示循环必定成立。
continue用于跳出该次循环,break用于跳出循环。
如果条件判断语句永远为True,循环语句会无限地执行下去。
循环时使用else,在循环条件为False时执行else语句块。
Counter模块
from collections import Counter
主要功能:可以支持方便、快速的计数,将元素数量统计,然后计数并返回一个字典,键为元素,值为元素个数。
from collections import defaultdict
Python中通过Key访问字典,当Key不存在时,会引发‘KeyError’异常。为了避免这种情况的发生,可以使用collections类中的defaultdict()方法来为字典提供默认值。设置default_factory为int,使得defaultdict可以用于计数,字符串中的字母第一次出现时,字典中没有该字母,default_factory函数调用int()为其提供一个默认值0,加法操作将计算出每个字母出现的次数。
divmod()
divmod() 函数把除数和余数运算结果结合起来,返回一个包含商和余数的元组(a // b, a % b)
enumerate()
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
[0 ]* n与[0 for _ in range(n)]的区别与联系
创建二维数组 以及 python中[0 ]* n与[0 for _ in range(n)]的区别与联系_[0 for _ in range(100)]是什么意思-CSDN博客
not 和 is None的区别
ACM模式
【ACM模式】牛客网ACM机试模式Python&Java&C++主流语言OJ输入输出案例代码总结-CSDN博客
第一行组数接空格分隔的两个正整数
2
1 5
10 20
t = int(input())
for i in range(t):
num = list(map(int,input().split(" ")))
print(sum(num))
空格分隔的两个正整数为0 0 结束
1 5
10 20
0 0
while True:
try:
num = list(map(int,input().split(" ")))
if num[0] == num[1] == 0:
break
print(sum(num))
except:
break
华为机试真题
满二叉树查找(100)
nums = list(map(int,input().split()))
nums.sort()
key = int(input())
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution(object):
def bulidTree(self, nums):
if not nums:
return
midIdx = len(nums)//2
root = TreeNode(nums[midIdx])
root.val = nums[midIdx]
root.left = self.bulidTree(nums[:midIdx])
root.right = self.bulidTree(nums[midIdx+1:])
return root
def search(self, root, key, path):
if root.val != key and root.left is None and root.right is None:
path += 'N'
return path
if key == root.val:
path += 'Y'
return path
if key < root.val and root.left is not None:
path += 'L'
return self.search(root.left, key, path)
if key > root.val and root.right is not None:
path += 'R'
return self.search(root.right, key, path)
solution = Solution()
root = solution.bulidTree(nums)
path = 'S'
result = solution.search(root, key, path)
print(result)
传统做法:构造出二叉树,按照二分法进行查找
另一种思路:无需构造二叉树,按照二分法进行查找即可
nums = list(map(int,input().split()))
nums.sort()
key = int(input())
class Solution(object):
def search(self, nums, key, path):
if len(nums) == 1 and key!= nums[0]:
path += 'N'
return path
mid = len(nums)//2
if key == nums[mid]:
path += 'Y'
return path
if key < nums[mid]:
path += 'L'
return self.search(nums[:mid], key, path)
if key > nums[mid]:
path += 'R'
return self.search(nums[mid+1:], key, path)
x = Solution()
result = x.search(nums, key, 'S')
print(result)计算云服务DI值(200分)
# 输入获取
m, n = map(int, input().split())
tree = {}
# 树节点
class Node:
def __init__(self):
self.major_count = 0 # 该节点的严重问题数量
self.minor_count = 0 # 该节点的一般问题数量
self.children = set() # 该节点的子节点集合
# 建树
def buildTree():
for _ in range(n):
# Ai节点的父节点是Bi
# Ai节点level级别问题新增count个
Ai, Bi, level, count = input().split()
# 获取Ai节点对象,若不存在则新建
tree.setdefault(Ai, Node())
# 获取Bi节点对象,若不存在则新建
tree.setdefault(Bi, Node())
if level == '0':
# Ai节点的严重问题数量+count
tree[Ai].major_count += int(count)
else:
# Ai节点的一般问题数量+count
tree[Ai].minor_count += int(count)
# Bi的子节点增加一个Ai
tree[Bi].children.add(Ai)
def bfs(rootName):
queue = [rootName]
major_count = 0
minor_count = 0
while queue:
nodeName = queue.pop(0)
node = tree[nodeName]
major_count += node.major_count
minor_count += node.minor_count
for child in node.children:
queue.append(child)
return major_count, minor_count
def dfs(nodeName):
node = tree[nodeName]
major_count = node.major_count
minor_count = node.minor_count
for child in node.children:
tmp = dfs(child)
major_count += tmp[0]
minor_count += tmp[1]
return major_count, minor_count
# 算法入口
def solution():
# 建树
buildTree()
# 名称为"*"的节点的子节点即为云服务节点
clouds = tree["*"].children
# 记录题解:风险云服务个数
ans = 0
# 遍历云服务节点
for cloudName in clouds:
# 遍历云服务树,树的遍历有两种方式:dfs或bfs
# 如果云服务树的层级过深,dfs可能会栈内存溢出,因此更推荐bfs
# major_count, minor_count = dfs(cloudName)
major_count, minor_count = bfs(cloudName)
# DI值 = 5 × 严重问题数+2 × 一般问题数
DI = major_count * 5 + minor_count * 2
# 当云服务DI值小于等于阈值时才准许云服务发布,否则视为风险云服务
if DI > m:
ans += 1
return ans
# 算法调用
print(solution())