LeetCode Weekly Contest 201

5483. 整理字符串

题目难度Easy
给你一个由大小写英文字母组成的字符串 s 。

一个整理好的字符串中，两个相邻字符 s[i] 和 s[i + 1] 不会同时满足下述条件：

0 <= i <= s.length - 2
s[i] 是小写字符，但 s[i + 1] 是相同的大写字符；反之亦然 。
请你将字符串整理好，每次你都可以从字符串中选出满足上述条件的 两个相邻 字符并删除，直到字符串整理好为止。

请返回整理好的 字符串 。题目保证在给出的约束条件下，测试样例对应的答案是唯一的。

注意：空字符串也属于整理好的字符串，尽管其中没有任何字符。

示例 1：

输入：s = “leEeetcode”
输出：“leetcode”
解释：无论你第一次选的是 i = 1 还是 i = 2，都会使 “leEeetcode” 缩减为 “leetcode” 。
示例 2：

输入：s = “abBAcC”
输出：""
解释：存在多种不同情况，但所有的情况都会导致相同的结果。例如：
“abBAcC” --> “aAcC” --> “cC” --> “”
“abBAcC” --> “abBA” --> “aA” --> “”
示例 3：

输入：s = “s”
输出：“s”

提示：

1 <= s.length <= 100
s 只包含小写和大写英文字母

思路

模拟

代码

class Solution {
    private int checkValid(String s) {
        int n = s.length(), i = 0;
        for (i=0; i<n-1; ++i) {
            if (Math.abs(s.charAt(i) - s.charAt(i+1)) == Math.abs('a' - 'A')) {
                return i;
            }
        }
        return -1;
    }
    
    public String makeGood(String s) {
        while (true) {
            int tmp = checkValid(s);
            if (tmp == -1) {
                return s;
            }
            s = s.substring(0, tmp) + s.substring(tmp+2, s.length());
        }
    }
}

5484. 找出第 N 个二进制字符串中的第 K 位

题目难度Medium
给你两个正整数 n 和 k，二进制字符串 Sn 的形成规则如下：

S1 = “0”
当 i > 1 时，Si = Si-1 + “1” + reverse(invert(Si-1))
其中 + 表示串联操作，reverse(x) 返回反转 x 后得到的字符串，而 invert(x) 则会翻转 x 中的每一位（0 变为 1，而 1 变为 0）

例如，符合上述描述的序列的前 4 个字符串依次是：

S1 = “0”
S2 = “011”
S3 = “0111001”
S4 = “011100110110001”
请你返回 Sn 的 第 k 位字符 ，题目数据保证 k 一定在 Sn 长度范围以内。

示例 1：

输入：n = 3, k = 1
输出：“0”
解释：S3 为 “0111001”，其第 1 位为 “0” 。
示例 2：

输入：n = 4, k = 11
输出：“1”
解释：S4 为 “011100110110001”，其第 11 位为 “1” 。
示例 3：

输入：n = 1, k = 1
输出：“0”
示例 4：

输入：n = 2, k = 3
输出：“1”

提示：

1 <= n <= 20
1 <= k <= 2^n - 1

思路

递归

代码

class Solution {
    private char invertChar(char ch) {
        if (ch == '1') {
            return '0';
        } else {
            return '1';
        }
    }
    
    public char findKthBit(int n, int k) {
        if (n == 1) {
            return '0';
        }
        int len = (1 << n) - 1, half = (1 << (n-1)) - 1;
        if (k-1 == half) {
            return '1';
        }
        if (k-1 < half) {
            return findKthBit(n-1, k);
        } else {
            return invertChar(findKthBit(n-1, len - k + 1));
        }
    }
}

5471. 和为目标值的最大数目不重叠非空子数组数目

题目难度Medium
给你一个数组 nums 和一个整数 target 。

请你返回 非空不重叠 子数组的最大数目，且每个子数组中数字和都为 target 。

示例 1：

输入：nums = [1,1,1,1,1], target = 2
输出：2
解释：总共有 2 个不重叠子数组（加粗数字表示） [1,1,1,1,1] ，它们的和为目标值 2 。
示例 2：

输入：nums = [-1,3,5,1,4,2,-9], target = 6
输出：2
解释：总共有 3 个子数组和为 6 。
([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。
示例 3：

输入：nums = [-2,6,6,3,5,4,1,2,8], target = 10
输出：3
示例 4：

输入：nums = [0,0,0], target = 0
输出：3

提示：

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
0 <= target <= 10^6

思路

贪心。子数组nums[i...j]的和用前缀和pres[j] - pres[i]得到。遍历nums数组，用哈希表保存之前的前缀和，设当前前缀和为preSum，如果preSum - target在哈希表中，则找到了长度最短的符合条件的子数组，将哈希表清空，从下一个数组元素开始的子数组中寻找新的符合目标子数组。
设nums.length = n，则时间复杂度为O(n).

代码

class Solution {
    public int maxNonOverlapping(int[] nums, int target) {
        int preSum = 0, ret = 0;
        HashSet<Integer> pres = new HashSet<>();
        pres.add(0);
        for (int num: nums) {
            preSum += num;
            if (pres.contains(preSum - target)) {
                ++ret;
                pres.clear();
                preSum = 0;
            }
            pres.add(preSum);
        }
        return ret;
    }
}

5486. 切棍子的最小成本

题目难度Hard
有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

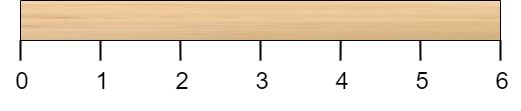
给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

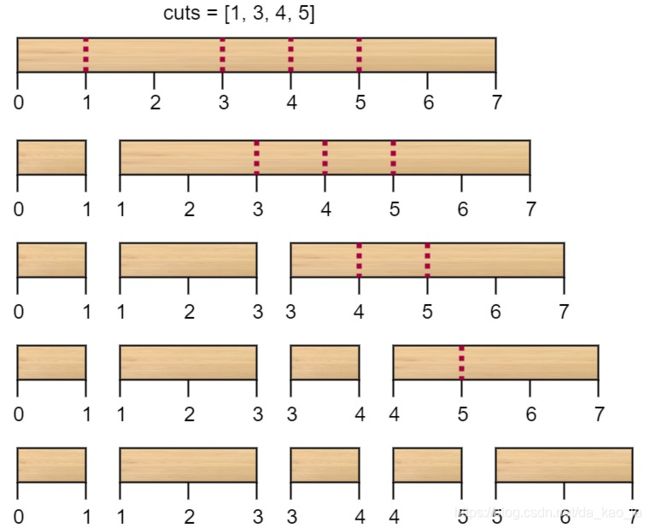
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
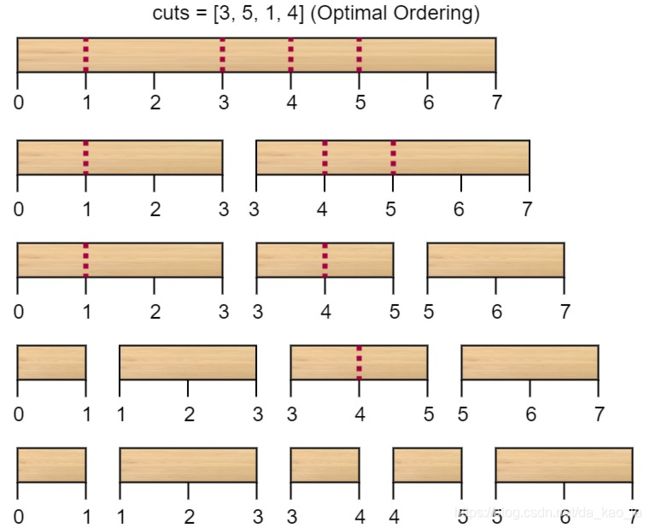
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。
示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4，6，5，2，1] 的总成本 = 22，是所有可能方案中成本最小的。
提示：
2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同

思路

动态规划. dp[i][j]表示合并cuts[i]到cuts[j]之间的区间的最小成本。按长度从小到大遍历每个区间，对于每个区间遍历每一个可能的划分点。设cuts.length = m，则时间复杂度为O(n^3).
比赛的时候一直在想哈夫曼树，但是由于这里有限制只能相邻的区间合并，因此用类似POJ 3253 Fence Repair（哈夫曼树，最小堆）那样的哈夫曼树的优先队列解法不可行。

代码

class Solution {
    public int minCost(int n, int[] cuts) {
        int m = cuts.length;
        Arrays.sort(cuts);
        int[][] dp = new int[m+2][m+2];
        for (int len=2; len<=m+1; ++len) {
            for (int j=0; j<=m+1-len; ++j) {
                dp[j][j+len] = Integer.MAX_VALUE;
                for (int k=j+1; k<j+len; ++k) {
                    int left = j == 0? 0: cuts[j-1], right = j+len == m+1? n: cuts[j+len-1];
                    dp[j][j+len] = Math.min(dp[j][j+len], dp[j][k] + dp[k][j+len] + right - left);
                }
            }
        }
        return dp[0][m+1];
    }
}