km算法入门

km算法入门

本文知识均由笔者自学，文章有错误之处请不吝指出。

 

笔者刷数模题的时候有一道题考到了“二分图最大权分配”，需要用到KM算法，但是书上对KM算法的介绍又臭又长，更何况有些同学“匈牙利算法”也没学过（由匈牙利数学家Edmonds提出），自然难以理解所谓的KM算法。本文旨在用通俗易懂的语言，向读者介绍匈牙利算法和KM算法。

 

一、匈牙利算法

匈牙利算法用于解决什么问题？

匈牙利算法用于解决二分图的最大匹配问题。

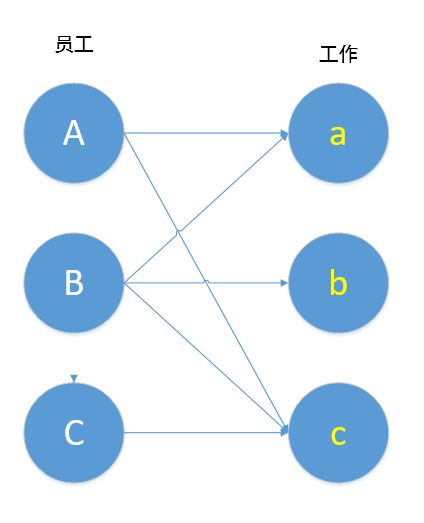
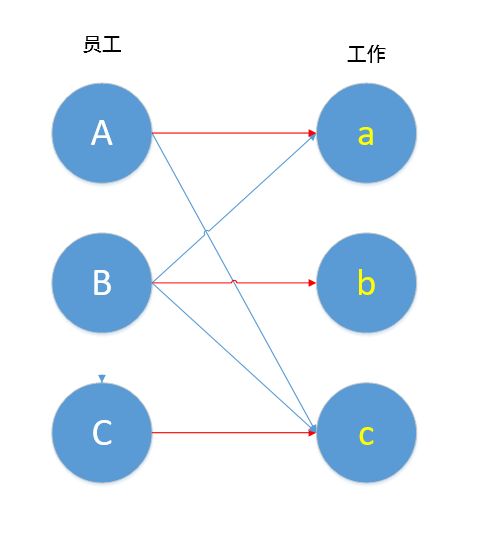
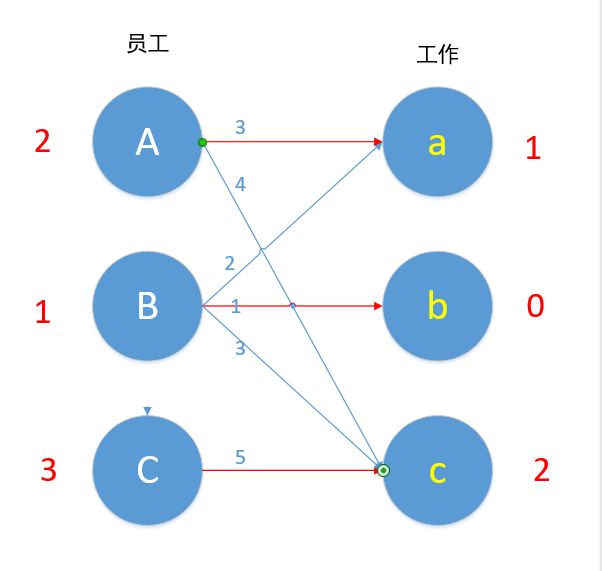
什么是二分图？我们不妨来考虑这样一个问题，在一家公司里，有员工A,B,C，有三种工作a,b,c，如果员工和工作之间有线相连，则代表员工能胜任这份工作。

如图所示，员工A能胜任a,c工作，员工B能胜任a,b,c工作，而员工C只能胜任c工作。

上图就是所谓的“二分图”（请忽略图中箭头），简单的说，上图可划分为两个集合{员工}，{工作}，两个集合之间的元素可以相连，同一个集合内的元素不能相连。

下面请解决这样一个问题：请给出一个方案，让尽可能多的员工有不同的工作做。“匈牙利算法”的出现就是为了解决这个问题。

下面给出这个问题的解决方案：（读者看到这里可能会想，解决这个问题不是很简单吗？A→a,B→b，C→c不就好了？请注意：任何算法的给出都是为了规整化一个问题的解决步骤，其目的是为了在问题规模越来越大时算法对其仍然适用，如果公司有10个员工或者更多，读者想必不能一眼看出答案，此时，算法的作用便体现出来了。）

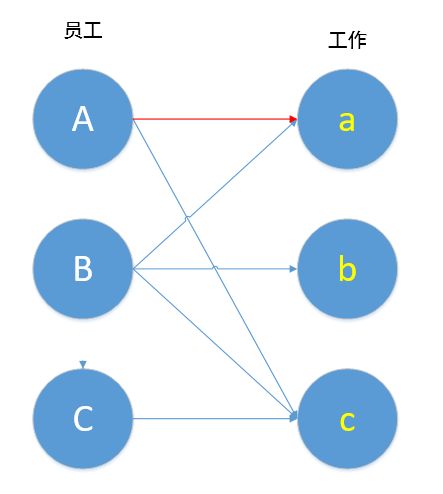
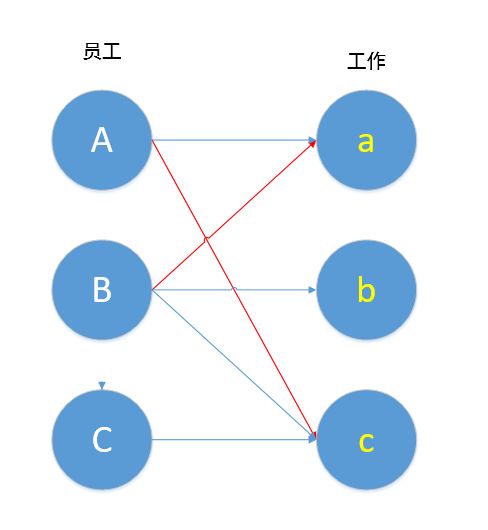
我们先帮A找工作做，不妨先帮A连上a（红线表示此时两者已经匹配），表示A去做a工作。

  

接下来我们帮B找工作做，B的第一条线跟a相连，B也想做工作a。

这时候就发生了冲突（collision），如何解决呢？

“匈牙利算法”指出 通过一条增广路径，通过取反操作，我们就能匹配更多的点。

什么是增广路径？增广路径是指，由一个未匹配的顶点开始，经过若干个匹配顶点，最后到达对面集合的一个未匹配顶点的路径，即这条路径将两个不同集合的两个未匹配顶点通过一系列匹配顶点相连。

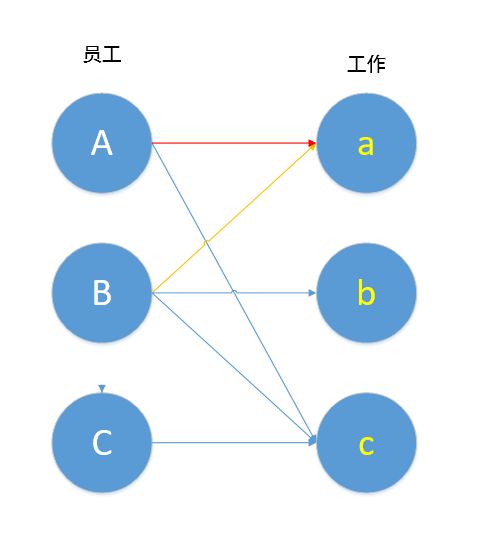
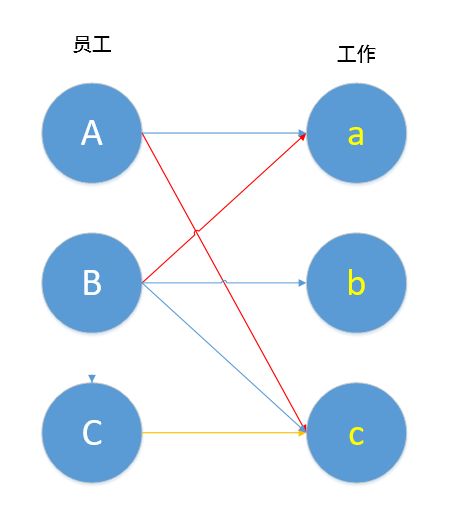
比如此题中，B想做工作a，于是A想着换一个工作，我们连上A，c。

 

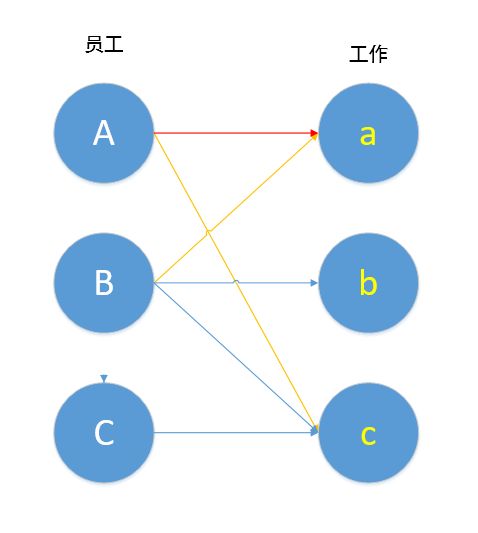
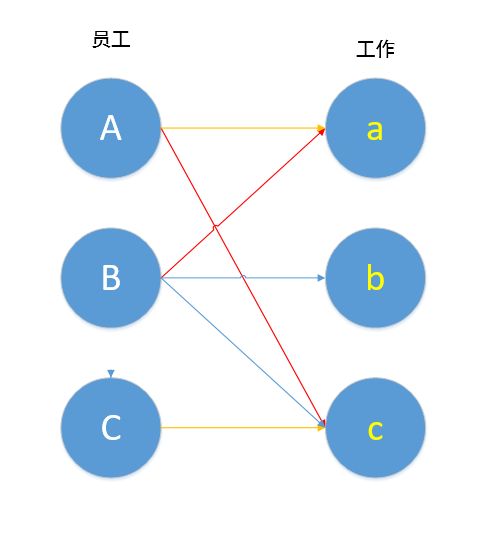
如图，B→a→A→c 其中B,c未匹配，A，a已匹配，按照定义，这就是一条增广路径，我们对其进行取反操作，就变成了下图。

 

取反操作为我们带来了什么？原本只有一边匹配，现在有两边匹配了，而且冲突也解决了，这就是匈牙利算法的妙处，我们能通过不停的寻找这样一条增广路径，从而找到二分图的最大匹配。

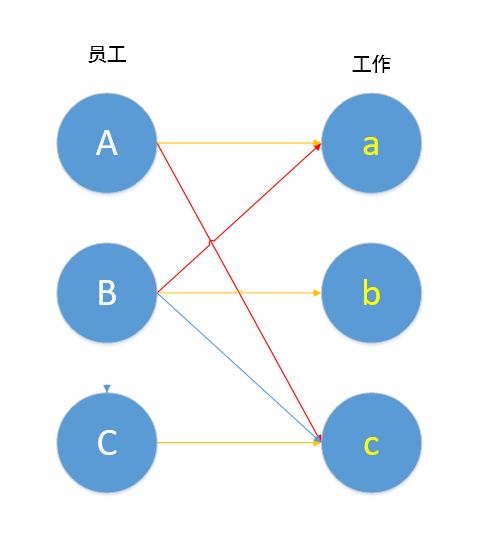
下面我们继续寻找增广路径。

最终，我们得到了一个最大匹配：A匹配a，B匹配b，C匹配c，就算集合中的元素很多很多，我们仍能通过匈牙利算法得到该二分图的最大匹配。

二、KM算法

现在我们来考虑另外一个问题：如果每个员工做每件工作的效率各不相同，我们如何得到一个最优匹配使得整个公司的工作效率最大呢？

这种问题被称为带权二分图的最优匹配问题，可由KM算法解决。

比如上图，A做工作a的效率为3，做工作c的效率为4......以此类推。

不了解KM算法的人如何解决这个问题？我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可。这不失为一个解决方案，但是，如果公司员工的数量越来越多，此种算法的实行难度也就越来越大，我们必须另辟蹊径：KM算法。

KM算法解决此题的步骤如下所示：

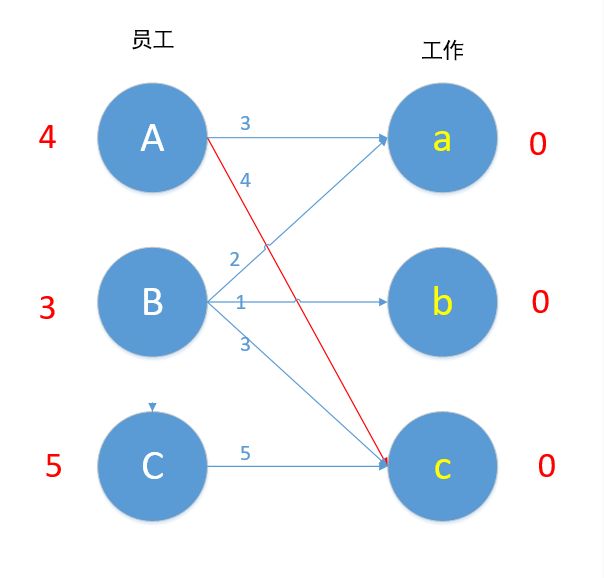
1.首先对每个顶点赋值，将左边的顶点赋值为最大权重，右边的顶点赋值为0。

如图，我们将顶点A赋值为其两边中较大的4。

2.进行匹配，我们匹配的原则是：只与权重相同的边匹配，若是找不到边匹配，对此条路径的所有左边顶点-1，右边顶点+1，再进行匹配，若还是匹配不到，重复+1和-1操作。（这里看不懂可以跳过，直接看下面的操作，之后再回头来看这里。）

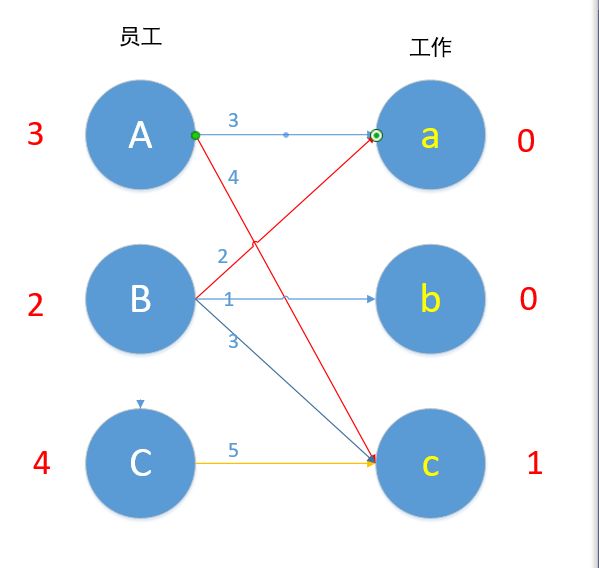
对A进行匹配，符合匹配条件的边只有Ac边。

匹配成功！

接下来我们对B进行匹配，顶点B值为3，Bc边权重为3，匹配成~ 等等，A已经匹配c了，发生了冲突，怎么办？我们这时候第一时间应该想到的是，让B换个工作，但根据匹配原则，只有Bc边 3+0=0 满足要求，于是B不能换边了，那A能不能换边呢？对A来说，也是只有Ac边满足4+0=4的要求，于是A也不能换边，走投无路了，怎么办？

从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个员工找到他们工作效率最高的工作，但是，有些工作会冲突，比如现在，B员工和A员工工作c的效率都是最高，这时我们应该让A或者B换一份工作，但是这时候换工作的话我们只能换到降低总体效率值的工作，也就是说，如果令R=左边顶点所有值相加，若发生了冲突，则最终工作效率一定小于R，但是，我们现在只要求最优匹配，所以，如果A换一份工作降低的工作效率比较少的话，我们是能接受的（对B同样如此）。

在KM算法中如何体现呢？

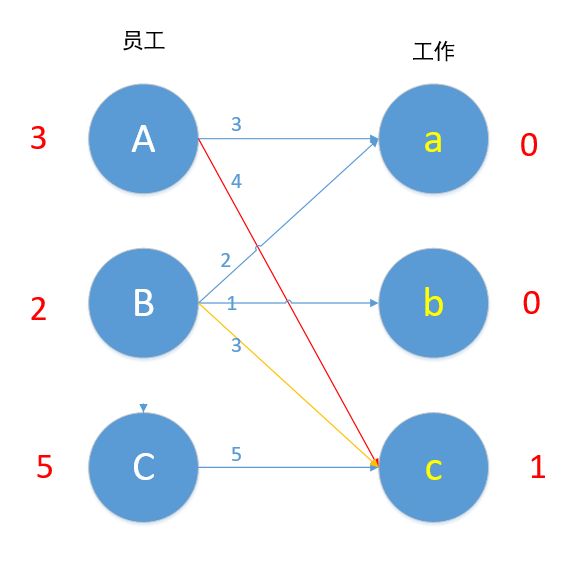
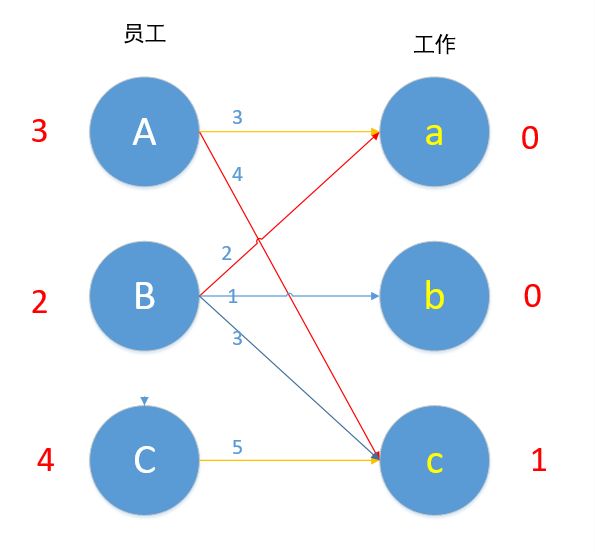
现在参与到这个冲突的顶点是A,B和c，令所有左边顶点值-1，右边顶点值+1，即 A-1,B-1. c+1，结果如下图所示。

我们进行了上述操作后会发现，若是左边有n个顶点参与运算，则右边就有n-1个顶点参与运算，整体效率值下降了1*（n-（n-1））=1，而对于A来说，Ac本来为可匹配的边，现在仍为可匹配边（3+1=4），对于B来说，Bc本来为可匹配的边，现在仍为可匹配的边（2+1=4），我们通过上述操作，为A增加了一条可匹配的边Aa，为B增加了一条可匹配的边Ba。

现在我们再来匹配，对B来说，Ba边 2+0=2，满足条件，所以B换边，a现在为未匹配状态，Ba匹配！

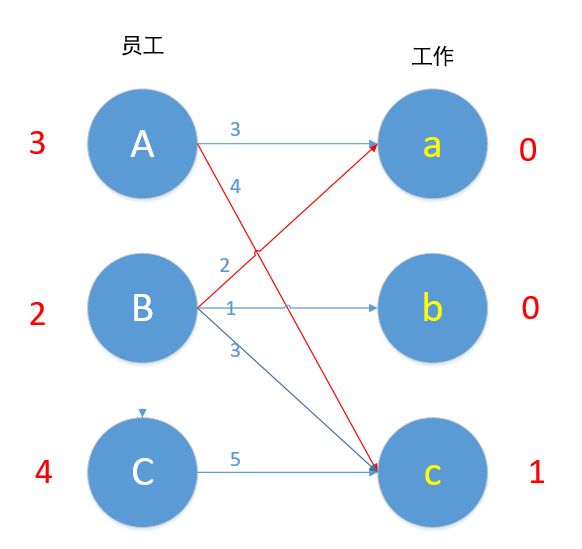
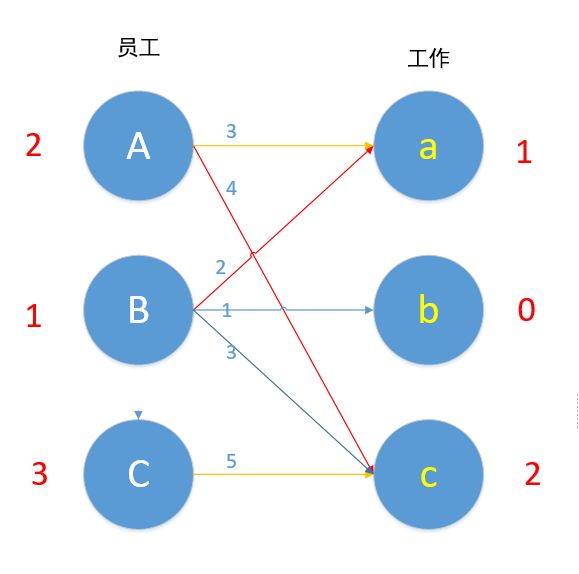
我们现在匹配最后一条边C，Cc 5+1！=5，C边无边能匹配，所以C-1。

现在Cc边 4+1=5，可以匹配，但是c已匹配了，发生冲突，C此时不能换边，于是便去找A，对于A来说，Aa此时也为可匹配边，但是a已匹配，A又去找B。

  

B现在无边可以匹配了，2+0！=1 ，现在的路径是C→c→A→a→B，所以A-1,B-1,C-1,a+1，c+1。如下图所示。

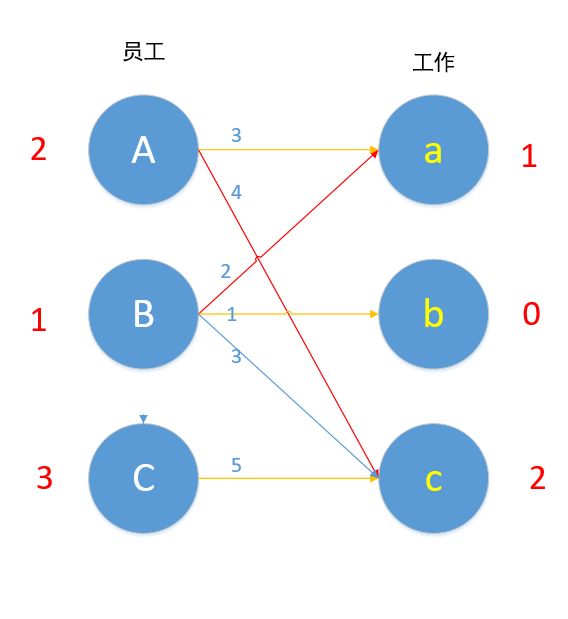
对于B来说，现在Bb 1+0=1 可匹配！

使用匈牙利算法，对此条路径上的边取反。

如图，便完成了此题的最优匹配。

读者可以发现，这题中冲突一共发生了3次，所以我们一共降低了3次效率值，但是我们每次降低的效率值都是最少的，所以我们完成的仍然是最优匹配！

这就是KM算法的整个过程，整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终我们完成的就是最优匹配！

PS：笔者此文旨在用通俗易懂的语言解释匈牙利算法和KM算法，所以对部分定理未加以证明，甚至有的部分一笔带过，这是为了全文的流畅性考虑，不专业之处请多多谅解。

转载自：https://www.cnblogs.com/logosG/p/logos.html