合唱队问题的求解——华为OJ题目

一、问题的描述

以下是原题目描述。要求计算最少出列多少位同学，使得剩下的同学排成合唱队形

说明：
N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。 
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，他们的身高分别为T1，T2，…，TK，   则他们的身高满足存在i（1<=i<=K）使得TiTi+1>......>TK。 
     你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。 

二、解题思路分析

        由于给定的序列是任意的，因此每一个同学都可能是出队的同学。观察结果要求，第i位同学比较特殊，是左右两边的分割点。因此思路就从第i位同学开始，依次假定每一位同学是第i个同学的情况下，寻找该种情况下的最少出队同学人数。等每个同学均作为第i个同学搜索后，所得到的出队最少人数会不断更新，最终得到最优结果。

        上面的分析解决了整体上的解题思路，接下来为了得到在固定i同学情况下，如何求最少出队序列。应该分两边来考虑，左边的最少出队人数和右边的最少出队人数，加起来的和即为总共最少出队人数。分析，对于i左边的同学，应该均比右边的同学低，因此如果符合比右边同学低的人可以保留下来，但是如果高于右边的同学就必须出队。但有一种情况比较容易忽视，即低于右边人的同学也可能出队，因为有可能他保留下来了，会导致他左边更多的人出队。

        对于i右边的同学，采用同样的思路来进行。因此可以采用两个递归函数求解，一个求解i左边的最少出队人数，一个求解i右边的最少出队人数。

三、程序源代码与说明

     在代码中设置了两个递归函数，分别对应上面分析的求解两边的最少出队人数，int digui1(int * a,int i,int p,int ch,int k)函数求解元素p左边的最少出队人数，ch记录当前以出队人数，int digui2(int * a,int i,int p,int ch,int k)函数求解元素p右边的最少出队人数。minch1变量记录左边的最少出队人数，minch2变量记录右边的最少出队人数。这两个变量会在递归过程中不断更新。另外主函数中，通过一个循环，依次设定每一个元素为i元素，执行递归过程。

#include "stdio.h"
#include "stdlib.h"
int digui1(int * a,int i,int p,int ch,int k);
int digui2(int *a, int len,int i,int p,int ch,int k);
int minch1=0,minch2=0;
void main()
{
int *a,num=0,i=0,j=0,p=0,ch=0,minch=0;
scanf("%d",&num);
minch=num;
a=(int *)malloc(num*sizeof(int));
for (i=0;i{
scanf("%d",&a[i]);
}
for (i=1;i{
minch1=num;
minch2=num;
digui1(a,i-1,i,0,i);
digui2(a,num,i+1,i,0,i);
ch=minch1+minch2;
if (ch{
minch=ch;
}
}
printf("%d\n",minch);
}
int digui1(int * a,int i,int p,int ch,int k)
{
if(i==0)
{
if (a[i]{
if(chminch1=ch;
}
else
{
ch++;
if(chminch1=ch;
}
return 0;
}
else
{
if (a[i]{
digui1(a,i-1,i,ch,k); //保留i位置的人
digui1(a,i-1,p,ch+1,k);//i位置的人出队
}
else
{
digui1(a,i-1,p,ch+1,k);
}
return 0;
}


}
int digui2(int *a, int len,int i,int p,int ch,int k)
{
if(i==len-1)
{
if (a[i]{
if(chminch2=ch;
}
else
{
ch++;
if(chminch2=ch;
}
return 0;
}
else
{
if (a[i]{
digui2(a,len,i+1,i,ch,k);
digui2(a,len,i+1,p,ch+1,k);
}
else
{
digui2(a,len,i+1,p,ch+1,k);
}
return 0;
}
}

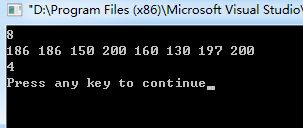
四、程序运行结果

                          图1 程序运行结果