数据结构——图—最小生成树(普里姆算法和克鲁斯卡尔算法)
最小生成树
传送门(图的遍历)http://blog.csdn.net/qq_33329316/article/details/53573798
传送门(图的概念和图的储存)http://blog.csdn.net/qq_33329316/article/details/53560874
在理解最小 生成树的概念之前首先应该理解一个概念生成树
生成树
一个图的生成树可以这样说:
包括了图中的所有节点,所有节点之间都有边,但是没有连通图;
就是有 N个顶点 有N-1个边;
最小生成树呢
最小生成树就是这些生成树的边上的权值之和最小的一棵树;
最小生成树有什么用呢?
首先做一个假设;你要去一个景点游玩,怎么样选择一条路才能使你走到最少而且走完这些呢?
这就是最小生成树的原理,怎么样才能最少的遍历结束所有节点呢?
介绍两种算法
1.Prim算法
2.Kruskal算法
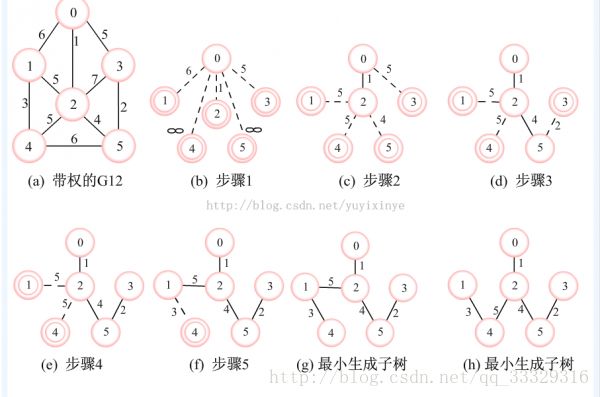
Prim算法
思想
设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
根据代码具体解释一下就是:首先建立两个数组 adjvex lowcost;
lowcost数组
1.数组里面存放权值,具体的说他是存放目前生成树中的所以顶点到各个顶点之间的距离;
2.比如lowcost[1]他就代表目前生成树中有的顶点到顶点1的最近距离;
3.如果顶点已经在生成树种那么他的.lowcost数组中对应位置的权值为0(有了自己自己自己就是0喽)
4.什么是生成树中的顶点就是在下面函数中我们把它的lowcost[x]设置为0的店一会会有解释;
adjvex数组
1.在adjcex算法中我们存放的是什么?他里面存放的是当前顶点到那个顶点最近权值最小;
注意上面是当前当前 他是在不停的变化的 上面的lowcost数组也是;
2.比如adjvex[2] =7,他的意思就是当前2顶点到7顶点最近;
邻接矩阵的算法实现
/*
函数解释;
首先我们初始化了 adjvex数组和 lowcost数组
然后我们从0顶点开始所以生成树种之后0节点low数组中我们先赋值进去赋值就是目前生成树中有的顶点,因为目前顶点中只有0顶点所以赋值是0顶点到 其他顶点的距离。注意这里0顶点已经进入生成树所以我们比较的时候就不比较他了
然后初始化0顶点全部为0现在不知道谁到谁权值最小;
然后就是For循环;它先初始化了一个值MIN这个值我们把它设置成全局变量;
设置的越大越好;
然后用这个函数
j = 1; k = 0;
while( j < p->N_v )//循环全部顶点
{
if(lowcost[j]!=0 && lowcost[j] < min)
{
min = lowcost [j];//让当前权值成为最小值
k = j;//当前最小值的下标存入K
//printf("目前最小值MIN为%d\n",min);
}
j++;
}
遍历所有lowcost[j]中的权值;找出最小的权值的店;这个下标就代表的第几个顶点 min 就是最小权值;K就是当前就是当前找到距离生成树中顶点距离最短的一个顶点;adjves[k]就是对应的当前树种的节点;
然后后面的函数就是一当前的K顶点为刚的0顶点在操作一遍;把K顶点加入了生成树;那么los数组中的对应各个顶点的最小权值要和K顶点的比较并且加入最小的-这就是下面函数的意思,然后继续循环知道循环为止
*/
void MiniSpanTree(M_g *p)
{
int min,i,j,k,n;
int adjvex[M];
int lowcost[M];//保存距离各边最近的权值
lowcost[0] = 0;//初始化第一个权值为0,就是V0加入生成树
//当lowcost的值为0时说明这个下标的顶点已经加入的生成树
adjvex[0] = 0;//初始化第一个顶点下标为0
for(i = 1; i < p->N_v;i++)
{
lowcost[i] = p->arc[0][i];//v0距离各个边的权值距离存入数组
adjvex[i] = 0;
}
for(i = 1;iN_v;i++)
{
min = INFINITE;//初始化最小值
j = 1; k = 0;
while( j < p->N_v )//循环全部顶点
{
if(lowcost[j]!=0 && lowcost[j] < min)
{
min = lowcost [j];//让当前权值成为最小值
k = j;//当前最小值的下标存入K
//printf("目前最小值MIN为%d\n",min);
}
j++;
}
printf("当前顶点x中权值最小为y\n");
printf("(%d,%d),%d\n",adjvex[k],k,min);
lowcost[k] = 0;
printf("目前的最小值为\n");
for(n = 0; n < p->N_v;n++)
{
printf("%d\t",lowcost[n]);
}
printf("\n");
for(j = 1; j < p->N_v;j++)
{
if(lowcost[j]!= 0 && lowcost[j] > p->arc[k][j])
{
lowcost[j] = p->arc[k][j];//将较小的权值存入lowcost
adjvex[j] = k;//将K的下标存入adjvex
}
}
}
} Prim算法具体实现
#includeN_v;j++)
{
printf("%d\t",x->arc[i][j]);
}
putchar('\n');
}
}
void MiniSpanTree(M_g *p)
{
int min,i,j,k,n;
int adjvex[M];
int lowcost[M];//保存距离各边最近的权值
lowcost[0] = 0;//初始化第一个权值为0,就是V0加入生成树
//当lowcost的值为0时说明这个下标的顶点已经加入的生成树
adjvex[0] = 0;//初始化第一个顶点下标为0
for(i = 1; i < p->N_v;i++)
{
lowcost[i] = p->arc[0][i];//v0距离各个边的权值距离存入数组
adjvex[i] = 0;
}
for(i = 1;iN_v;i++)
{
min = INFINITE;//初始化最小值
j = 1; k = 0;
while( j < p->N_v )//循环全部顶点
{
if(lowcost[j]!=0 && lowcost[j] < min)
{
min = lowcost [j];//让当前权值成为最小值
k = j;//当前最小值的下标存入K
//printf("目前最小值MIN为%d\n",min);
}
j++;
}
printf("当前顶点x中权值最小为y\n");
printf("(%d,%d),%d\n",adjvex[k],k,min);
lowcost[k] = 0;
printf("目前的最小值为\n");
for(n = 0; n < p->N_v;n++)
{
printf("%d\t",lowcost[n]);
}
printf("\n");
for(j = 1; j < p->N_v;j++)
{
if(lowcost[j]!= 0 && lowcost[j] > p->arc[k][j])
{
lowcost[j] = p->arc[k][j];//将较小的权值存入lowcost
adjvex[j] = k;//将K的下标存入adjvex
}
}
}
}
int main(){
M_g *p;
p = (M_g*)malloc(sizeof(M_g));
onCreateM_g(p);
ergodic (p);
DFSTraverse (p);
MiniSpanTree(p);
return 0;
}
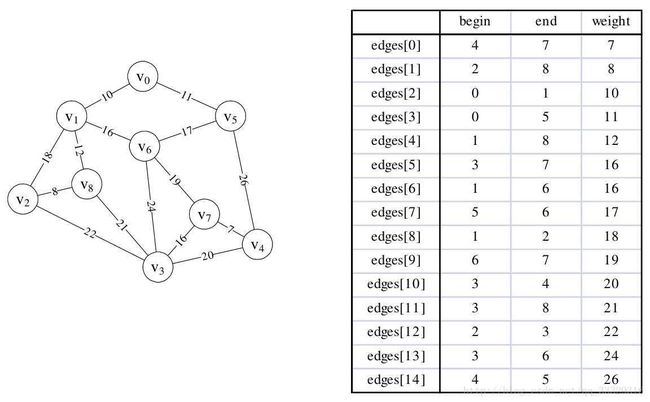
/*9 15
0 1 2 3 4 5 6 7 8
0 1 10
0 5 11
1 2 18
1 6 16
1 8 12
2 8 8
2 3 22
3 8 21
3 6 24
3 7 16
3 4 20
4 5 26
4 7 7
5 6 17
6 7 19
*/
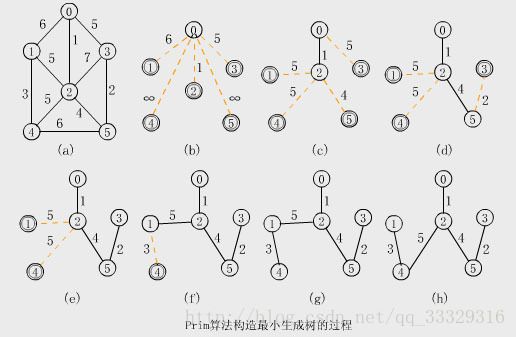
Kruskal算法
算法思想;
简单的说Prime算法是以点为出发点;而Kruskal算法就是以边为出发点
他的大概意思就是首先把顶点和边全部剥离;按照边上权值的由小到大依次排序;然后从最小权值的边开始查找顶点,然后把它们依次加入生成树。
邻接矩阵的算法实现
首先定义一个结构体数组生成图二
typedef struct
{
int begin;
int end;
int weight;
}Edge;
一个存放开始的顶点
一个存放结束的顶点
一个存放边的权值;
完美的概括了一个边
/*
函数解释;
首先,我们定义一个Edge数组存放边的信息;然后初始化parent数组;
Parent数组的作用就是存放顶点比如parent[0] = 1说明顶点0 和1 已经进入生成树了;
还有一个作用就是判断是否形成回路;
然后算法大概就是,按照比较同一个边上的两个顶点,如果通过了Find函数的判断说明4和7之间没有形成回路;
就把顶点输入parent数组中;
Find函数的意思大概就是 传入Parent数组和边的前顶点和后顶点判断;如果parent[f]的值大于0则继续循环;循环导等于0为止;因为当在parent数组下标对应的值为0的时候说明他目前没有进入树。同时也可以避免环路;
今天比较瞌睡具体明天改
int Find (int *parent,int f)
{
while(parent[f] > 0)
f = parent[f];
return f;
}
void MiniSpanTree(LinkdeGraph *p)
{
int i,n,m;
Edge edges[M];//存放边集数组
int parent[M];//定义一数组用来判断边与边是否形成环路
//这里应该有将邻接矩阵P转化的边集合转化为边集数组edges并且按照权值由大到小排列出图2的代码;太头疼没写;快速排序法就可以;
for(i = 0; i < p->n_e; i++)
{
parent[i] = 0;
}
for( i = 0; i < p->n_e; i++)
{
n = Find(parent,edges[i].begin);
m = Find(parent,edges[i].end);
if( n!=m)
{
parent[n] = m;
printf("(%d,%d),%d",edges[i].begin,edges[i].end,edges[i].weight);
}
}
}