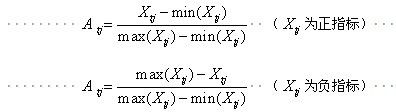BP神经网络（属于深度学习）

一、python代码自编BP神经网络

步骤：

1、初始化权值、阈值

2、正向传播到output

3、计算误差

4、反向传播得到梯度信息

5、根据梯度信息，更新权重、阈值

6、直到误差足够小或达到迭代次数，跳出循环，否则返回步骤2

7、显示epoch误差，绘图显示

   首先生成随机数据：

import numpy as np
x=np.random.random((100,4))#输入空间，4个属性，100个样本
y=x[:,0]**2 + x[:,1]*9 + np.sqrt(x[:,2]) + x[:,3]#输出空间

1、初始化权值（矩阵）、阈值（一维）：从输入层到隐层，从隐层到输出层

参数设置：输入层、隐层、输出层分别有多少个神经元、学习速率、循环次数

learning_rate = 0.01 #学习率
input_size = 4 #输入层神经元个数，对应4个属性：x.shape[1]
output_size = 1 #输出层神经元个数:y.ndim
hidden_size = 8 #隐层神经元个数（一般取输入神经元个数的两倍）
iter_num = 10000 #训练次数（循环次数）

# input_layer->hidden_layer
V = np.random.random((input_size,hidden_size)) #权重矩阵：四行八列
b1 = np.random.random((1,hidden_size)) 
#阈值（长度为8的向量）,。变成二维后方便在后面与二维矩阵做运算

#hidden layer-->output layer
W = np.random.random((hidden_size,output_size))  #权重矩阵
b2 = np.random.random((1,output_size)) 
#阈值：个数与sigmord函数个数有关

#自定义激活函数：
def sigmord(x):
     return 1/(1+np.exp(-x))

2、正向传播到output：输出包括输入层到隐层的输出和隐层到输出层的输出

输入神经元乘以对应的权重矩阵再加上项放到激活函数后得到隐层神经元的输出 求出 ：隐层神经元的输出+输出层神经元的输出 其中主要涉及的为矩阵的运算。

x0 = x[0]
y0 = y[0]
#隐层神经元的输出:
print(x0[np.newaxis,:].shape)
print(V.shape)
#x为一维，权重矩阵V为二维，需要添加新维度将x变为二维才能乘
alpha = x0[np.newaxis,:].dot(V) #矩阵乘法用dot；#隐层神经元输入
hidden_output = sigmord(alpha - b1)
print(hidden_output)

#输出层神经元的输出
beta = hidden_output.dot(W) #输出层神经元输入
y_pre = sigmord(beta - b2) #输出层神经元输出
print(y_pre)

sigmord函数的函数值在(0,1)之间，最开始生成的初始值y跨度比较大，比如

10.30756803,   1.86721183

而预测值的y由于进行了激活函数的计算变在了(0,1)之间，因此两者就会有较大的误差，因此进行数据标准化（此处采用极差标准化）

极差标准化方法：是经济统计分析中对正负指标标准化的一种处理方法，标准化后数值也在(0,1)之间

#数据标准化:对y进行极差标准化（sigmord函数性质决定）
#方法一：
from sklearn.preprocessing import MinMaxScaler
model = MinMaxScaler().fit(y[:,np.newaxis])
y_new = model.transform(y[:,np.newaxis])
#方法二：不想调用sklearn就直接自编：
# y_new = (y-y.min())/(y.max()-y.min())

3、计算误差

y0 = y_new[0]
cost = ((y0 - y_pre)**2)/2
cost

4、反向传播得到梯度信息

更新的公式：

#计算隐层到输出层的权重矩阵梯度项
#第一个公式
W_delta = learning_rate * (y_pre - y0) *y_pre\
*(1-y_pre) *hidden_output
# W_delta应该与W的形状一样，因此要转置
W_delta = W_delta.T 
#计算隐层到输出层的阈值梯度项
#第二个公式
b2_delta = -learning_rate * y_pre *(1-y_pre)*(y0-y_pre)

#计算输入层到隐层的权重矩阵梯度项
g = (y0-y_pre) * y_pre * (1-y_pre)
V_delta = learning_rate * hidden_output * (1-hidden_output)\
* x0[:,np.newaxis].dot(W.dot(g).T)
#W.dot(g)为8行1列，x0为一维，需要添加维度，维度一样后矩阵相加即为更新操作
#计算输入层到隐层的阈值梯度项
b1_delta = -learning_rate * hidden_output *(1-hidden_output)\
*W.dot(g).T

5、根据梯度信息，更新权重、阈值

W += W_delta  #W=W+W_delta
V += V_delta
b1 += b1_delta
b2 += b2_delta

6、直到误差足够小或达到迭代次数，跳出循环，否则返回步骤2（前面的代码为部分数据举例，以下代码综合前面的对所有数据加上循环后进行计算）

y_new = (y-y.min())/(y.max()-y.min())
all_cost=[]
for i in range(iter_num):
    x0 = x[i %100]
    y0 = y[0]
    alpha = x0[np.newaxis,:].dot(V) 
    hidden_output = sigmord(alpha - b1)
    beta = hidden_output.dot(W)
    y_pre = sigmord(beta - b2) 
#3.计算误差
    y0 = y_new[i %100]
    cost = ((y0 - y_pre)**2)/2
    cost = cost[0,0]
    all_cost.append(cost) #取出两个中括号中的数字
    while cost<=1e-19:
        break
#4.反向传播得到梯度信息
    W_delta = learning_rate * (y_pre - y0) *y_pre*(1-y_pre) *hidden_output
    W_delta = W_delta.T 
    b2_delta = -learning_rate * y_pre *(1-y_pre)*(y0-y_pre)
    g = (y0-y_pre) * y_pre * (1-y_pre)
    V_delta = learning_rate * hidden_output * (1-hidden_output)\
    * x0[:,np.newaxis].dot(W.dot(g).T)
    b1_delta = -learning_rate * hidden_output *(1-hidden_output)\
    *W.dot(g).T
#5.更新权重、阈值
    W += W_delta
    V += V_delta
    b1 += b1_delta
    b2 += b2_delta
    
    print(f'第{i}次 损失值为：{cost}'.center(50,'='))

7、显示epoch误差，绘图显示

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.figure(figsize=(15,3))
plt.title('BP神经网络误差情况')
plt.plot(range(len(all_cost)),all_cost)
plt.show()

Sklearn调用：

from sklearn.neural_network import MLPRegressor
model = MLPRegressor(hidden_layer_sizes=8).fit(x,y)
#random_state=None随机种子
model.coefs_ #权重矩阵
model.intercepts_ #阈值

import numpy as np
x_test =np.random.random((20,4))#输入空间，4个属性，100个样本
y_test =x_test[:,0]**2 + x_test[:,1]*9 + np.sqrt(x_test[:,2]) + x_test[:,3]#输出空间为10个样本

y_predict = model.predict(x_test)
import matplotlib.pyplot as plt
plt.plot(range(20),y_predict)
plt.plot(range(20),y_test)
plt.legend(['predict','real'])
plt.show()