你还在用二分法求2个鸡蛋100层楼的问题吗?
题目
2个鸡蛋,100层楼,如何用最少的试验次数得到在鸡蛋落下不碎的最高层数?这一据说曾被谷歌纳入校园招聘题库的经典面试题,想必许多人都曾遇到过,又有多少人与我一样,不加思索就直接回答用二分法查找的?
但是,二分法真的是最优试验方法吗?接下来我们来分析几种解法。
首先我们先认真看一下完整的题目(之前做过这道题的同学可以跳过这一步):
原题:两个软硬程度一样但未知的鸡蛋,它们有可能都在一楼扔下来就摔碎,也有可能从100层楼上扔下来也没事。有座100层的楼,要你用这两个鸡蛋确定哪一层是鸡蛋可以安全落下的最高位置。可以摔碎两个鸡蛋,在最坏情况下,如何用最少的试验次数得到鸡蛋落下不会被摔碎的最高层数?
解法
最笨的方法:遍历查找
把其中的一个鸡蛋,从第1层开始往下扔。如果第一层没碎,换到第2层扔;如果第2层没碎,换到第3层扔…假设第50层没碎,第51层碎了,说明鸡蛋落下不会摔碎的最高层数为第50层。
这个方法在最坏情况下,需要扔99次。
二分法
采用二分查找的方法:
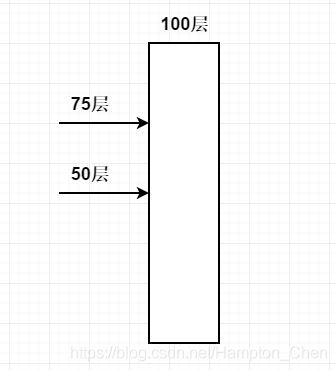
把第一个鸡蛋从一半楼层(50层)扔下。
如果鸡蛋碎了,则第二个鸡蛋就从第1层开始扔,一层一层增长,直到49层。
如果第一枚鸡蛋在50层没有被摔碎,则继续使用二分法,从剩余的楼层的一半(75层)开始往下扔…
在最坏情况下,这种二分法需要进行50次试验0。
平方根法
如何让第一个鸡蛋和第二个鸡蛋的尝试次数尽可能均衡?我们做一个平方根运算,100的平方根为10。
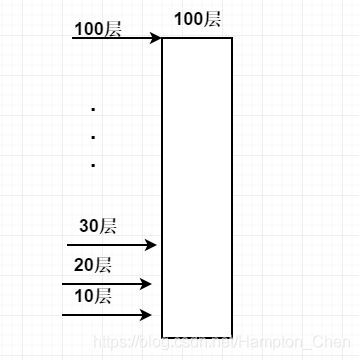
因此我们第一个鸡蛋每10层扔一次,第一次从第10层扔,没碎的话再加10层,即从20层扔…一直扔到100层。
第二个鸡蛋从第一个鸡蛋碎掉的n层往下9层,即n-9层开始一层一层往上试。
这种方法最好的情况为:第一个鸡蛋在第10层碎掉,尝试次数 1 + 9 = 10 次。
最坏的情况为:第一个鸡蛋在第100层碎掉,尝试次数为 10 + 9 = 19 次。
这样子看来平方根的方法算是比较好的方法,那么还有更好的方法吗?
反向思考
我们反向思考一下这个题目:假设题目存在最优解,这个最优解的最坏情况尝试x次,那么我们第一次扔要选择在第几层?
假设第一次扔在x+1层:如果第一个鸡蛋碎了,那么第二个鸡蛋就只能从第1层开始一层一层扔,一直扔到第x层。这样总共尝试了x+1次,与最优解的尝试x次相悖。
假设第一次在x-1层:如果第一个鸡蛋碎了,那么第2个鸡蛋就要从第1层开始扔,一直到x-2层,共尝试了x-2+1=x-1次,虽然没有超出假设次数,但似乎有些过于保守。
假设第一次扔在第x层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-1层。这样,我们总共尝试了x-1+1 = x次,刚刚好没有超出假设次数。
恰恰是从第x层开始扔,选择高一层或第一层都不合适。
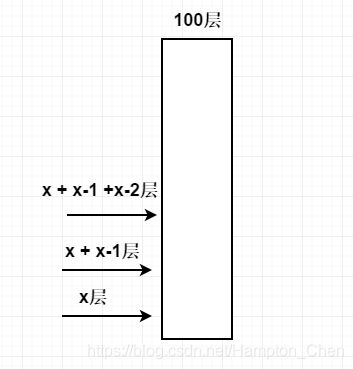
如果第一个鸡蛋没碎,问题就变成了:在100-x层楼往下扔,要求尝试次数不超过x-1次。
那么第二次的尝试次数的上限变为x-1次,所以第2次试验的楼层跨度为x-1层,真实层数为x+x-1层。
以此类推我们可以列出楼层的方程式: x + (x - 1) + (x - 2) + … + 1 = 100
接下来就是求解方程式,我们将这种方法称为解方程法:
解方程法
x + (x - 1) + (x - 2) + … + 1 = 100 => (x + 1) * x / 2 = 100
向上取整得到x=14
即最优解的最坏尝试次数为14次,第1个鸡蛋开始扔的层数也为14层。
第一个鸡蛋没碎的情况下,所尝试的楼层为:14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
假设鸡蛋不会被摔碎的最高楼层为55层,那么第一个鸡蛋尝试的楼层为14,27,39,50,60,在第60层碎了;
第二个鸡蛋从51层开始, 51,52,53,54,55,56,第56层碎了,则尝试次数为5 + 6 = 11 < 14
这道面试题的解法到此到一段落,现在你还会认为二分法是这道题的最优解吗?
其实这道题还可以衍生下面的问题:
总共有M层楼,N个鸡蛋,要找到鸡蛋不被摔碎的最高楼层,需要尝试几次?
这个问题就不在这里展开讨论了,大家可以自行尝试求解。