滴滴笔试-地下迷宫

滴滴在线笔试题目：

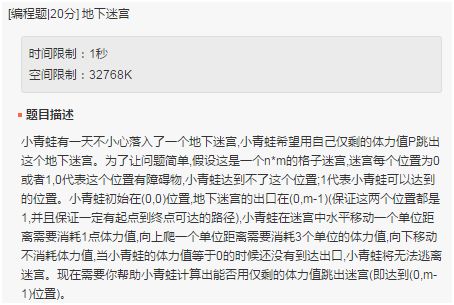
以下图片截图是滴滴2017秋招工程岗笔试题（算法工程师）在线编程题。我们先从最经典的走迷宫问题说起，随后求解此题目

经典都迷宫问题（java）

回溯法是一种不断尝试且及时纠正错误的搜索方法。下面的求解过程采用“回溯法”。我们这里采用一个栈来盛放已走过的点。原点入栈–>，从入口进入，出栈，每一次寻路从8个方向中去搜索可以通过的路径（这里0表示无障碍，可通过；1表示障碍，不能通过）。走过之后，原位置设为-1，表示已走过不能回去。当在此位置搜索完所有方向，都没有=0时。我们跳出循环，再从栈中出一个点，也就是回退一步，以此类推。
题目来自：这里写链接内容
（1）表示迷宫的数据结构
　　设迷宫为m行n列，利用数组maze[m][n]来表示一个迷宫，maze[i][j]=0或1，其中0表示通路，1表示不通。迷宫该数组四边都为1，代表迷宫四周都是墙。这样就可以保证每个点都有8个方向可以试探。
　　入口为（1,1），出口为（6,8）
　 1,1,1,1,1,1,1,1,1,1
1,0,1,1,1,0,1,1,1,1
1,1,0,1,0,1,1,1,1,1
1,0,1,0,0,0,0,0,1,1
1,0,1,1,1,0,1,1,1,1
1,1,0,0,1,1,0,0,0,1
1,0,1,1,0,0,1,1,0,1
1,1,1,1,1,1,1,1,1,1
（2）试探方向
　　迷宫中间每个点都有8个方向可以试探。其增量数组可以用一个8*2的二维数组move表述，表示对当前点而言,它周围8个点的行和列的坐标偏移量.具体值如下：
　　　　 x　y
0　0　1
1 1 1
2 1 0
3 1 -1
4 0 -1
5 -1 -1
6 -1 0
7 -1 1
在move数组中，x表示横坐标的增量，y表示纵坐标的增量。
（3）栈中存放元素的设计
　　栈中所存放的元素应该包含所到达的每点的坐标以及从该点沿哪个方向向下走的,可用一个类表示:

class Step{
     int x,y,d;
     public Step(int x,int y,int d) {
         this.x = x;//横坐标
         this.y = y;//纵坐标
         this.d = d;//方向
     }
 }

import java.util.Scanner;
import java.util.Stack;

/**
 * @author Home
 * 
 */
public class Main {

    public static void main(String[] args) {
        /*
         * Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m =
         * sc.nextInt(); int P = sc.nextInt(); int[][] maze = new int[n][m];
         * 
         * for(int i=0;i
        int[][] maze = { { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },
                { 1, 0, 1, 1, 1, 0, 1, 1, 1, 1 },
                { 1, 1, 0, 1, 0, 1, 1, 1, 1, 1 },
                { 1, 0, 1, 0, 0, 0, 0, 0, 1, 1 },
                { 1, 0, 1, 1, 1, 0, 1, 1, 1, 1 },
                { 1, 1, 0, 0, 1, 1, 0, 0, 0, 1 },
                { 1, 0, 1, 1, 0, 0, 1, 1, 0, 1 },
                { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 } };
        int[][] move = { { 0, 1 }, { 1, 1 }, { 1, 0 }, { 1, -1 }, { 0, -1 },
                { -1, -1 }, { -1, 0 }, { -1, 1 } };
        Stack stack = new Stack();
        int label = moveStep(maze, move,stack);
        if(label==1)
            for(Step s:stack){
                System.out.println(s.x+" "+s.y+" "+s.d);
            }
        else
            System.out.println("无通路！");
    }
    public static int moveStep(int[][] maze, int[][] move,Stack stack) {
        Step temp = new Step(1, 1, -1);
        stack.push(temp);
        while (!stack.isEmpty()) {
            temp = stack.pop();
            int x = temp.x;
            int y = temp.y;
            int d = temp.d + 1;
            while (d < move.length) {
                int i = x + move[d][0];
                int j = y + move[d][1];
                if (maze[i][j] == 0) {
                    temp = new Step(i, j, d);
                    stack.push(temp);
                    x = i;
                    y = j;
                    maze[x][y] = -1;
                    if (x == 6 && y == 8)
                        return 1;
                    else
                        d = 0;
                } else
                    d++;
            }
        }

        return 0;
    }

}

求解滴滴-地下迷宫（java）

import java.util.Stack;
import java.util.Scanner;
/*

 */


/**
 * @author Home
 *
 */
public class Solution {

    /**
     * @param args
     */
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int P = sc.nextInt();
        int[][] maze = new int[n][m];
        for(int i=0;ifor(int j= 0;jint[][] move = {{0,1},{0,-1},{1,0},{-1,0}};
        Stack stack = new Stack();
        int label = moveStep(maze,move,P,stack);
        if(label>0&&P>=0){
            System.out.println("P:"+P);
        for(Step s:stack)
            System.out.println(s.x+" "+s.y);
        }
        sc.close();
    }
    public static int moveStep(int[][] maze,int[][] move,int P,Stack stack){
        Step temp = new Step(0,0,-1);
        stack.push(temp);
        int m = maze.length;
        int n = maze[0].length;
        int p=0;
        while(!stack.isEmpty())
        {
            P+=p;
            temp = stack.pop();
            int x = temp.x;
            int y = temp.y;
            int d = temp.d+1;
            while(dint i = x+move[d][0];
                int j = y+move[d][1];
                //水平移动消耗p=1;上移动消耗p=3;下移动消耗p=0；
                if(d==0||d==1)
                    p=1;
                else if(d==3)
                    p=3;
                if(i<0||j<0||i>=m||j>=n){
                    d++;
                    continue;
                }

                //0：障碍物  1：通路
                if(maze[i][j]==1){
                    temp = new Step(i,j,d);
                    stack.push(temp);
                    x = i;
                    y = j;
                    maze[x][y] = -1;
                    P -= p;
                    if(i==0&&j==maze.length-1){
                        System.out.println(P);
                        return 1;
                    }else
                        d=0;

                }else
                    d++;

            }
        }
        System.out.println(P);
        return 0;

    }

}

求解过程还有问题，待完善。