运动规划之双向广度优先搜索
原理
双向广度优先搜索BidirectionalBreadthFirstSearch是对BFS的一种扩展,只是从起点和终点同时进行搜索而已。如下图所示:分别从青色(起点)和黄色(终点)进行搜索,直至它们相交。
例子
这个例子是在开源代码中找到的,给添加了一些注释;另外该算法虽然是使用python写的,但其实可以忽略掉一些辅助性的东西而关注于核心思想。
current_A = open_set_A.pop(list(open_set_A.keys())[0])
current_B = open_set_B.pop(list(open_set_B.keys())[0])
根据先进先出的原则弹出。
"""
Bidirectional Breadth-First grid planning
author: Erwin Lejeune (@spida_rwin)
See Wikipedia article (https://en.wikipedia.org/wiki/Breadth-first_search)
"""
import math
import matplotlib.pyplot as plt
show_animation = True
class BidirectionalBreadthFirstSearchPlanner:
def __init__(self, ox, oy, reso, rr):
"""
Initialize grid map for bfs planning
ox: x position list of Obstacles [m]
oy: y position list of Obstacles [m]
reso: grid resolution [m]
rr: robot radius[m]
"""
self.reso = reso
self.rr = rr
self.calc_obstacle_map(ox, oy)
self.motion = self.get_motion_model()
class Node:
def __init__(self, x, y, cost, pind, parent):
self.x = x # index of grid
self.y = y # index of grid
self.cost = cost
self.pind = pind
self.parent = parent
def __str__(self):
return str(self.x) + "," + str(self.y) + "," + str(
self.cost) + "," + str(self.pind)
def planning(self, sx, sy, gx, gy):
"""
Bidirectional Breadth First search based planning
input:
sx: start x position [m]
sy: start y position [m]
gx: goal x position [m]
gy: goal y position [m]
output:
rx: x position list of the final path
ry: y position list of the final path
"""
nstart = self.Node(self.calc_xyindex(sx, self.minx),
self.calc_xyindex(sy, self.miny), 0.0, -1, None)
ngoal = self.Node(self.calc_xyindex(gx, self.minx),
self.calc_xyindex(gy, self.miny), 0.0, -1, None)
open_set_A, closed_set_A = dict(), dict()
open_set_B, closed_set_B = dict(), dict()
open_set_B[self.calc_grid_index(ngoal)] = ngoal
open_set_A[self.calc_grid_index(nstart)] = nstart
while 1:
if len(open_set_A) == 0:
print("Open set A is empty..")
break
if len(open_set_B) == 0:
print("Open set B is empty")
break
current_A = open_set_A.pop(list(open_set_A.keys())[0])
current_B = open_set_B.pop(list(open_set_B.keys())[0])
c_id_A = self.calc_grid_index(current_A)
c_id_B = self.calc_grid_index(current_B)
closed_set_A[c_id_A] = current_A
closed_set_B[c_id_B] = current_B
# show graph
if show_animation: # pragma: no cover
plt.plot(self.calc_grid_position(current_A.x, self.minx),
self.calc_grid_position(current_A.y, self.miny), "xc")
plt.plot(self.calc_grid_position(current_B.x, self.minx),
self.calc_grid_position(current_B.y, self.miny), "xc")
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event:
[exit(0) if
event.key == 'escape' else None])
if len(closed_set_A.keys()) % 10 == 0:
plt.pause(0.001)
if c_id_A in closed_set_B:
print("Find goal")
meetpointA = closed_set_A[c_id_A]
meetpointB = closed_set_B[c_id_A]
break
elif c_id_B in closed_set_A:
print("Find goal")
meetpointA = closed_set_A[c_id_B]
meetpointB = closed_set_B[c_id_B]
break
# expand_grid search grid based on motion model
for i, _ in enumerate(self.motion):
breakA = False
breakB = False
node_A = self.Node(current_A.x + self.motion[i][0],
current_A.y + self.motion[i][1],
current_A.cost + self.motion[i][2],
c_id_A, None)
node_B = self.Node(current_B.x + self.motion[i][0],
current_B.y + self.motion[i][1],
current_B.cost + self.motion[i][2],
c_id_B, None)
n_id_A = self.calc_grid_index(node_A)
n_id_B = self.calc_grid_index(node_B)
# If the node is not safe, do nothing
if not self.verify_node(node_A):
breakA = True
if not self.verify_node(node_B):
breakB = True
if (n_id_A not in closed_set_A) and (n_id_A not in open_set_A) and (not breakA):
node_A.parent = current_A
open_set_A[n_id_A] = node_A
if (n_id_B not in closed_set_B) and (n_id_B not in open_set_B) and (not breakB):
node_B.parent = current_B
open_set_B[n_id_B] = node_B
rx, ry = self.calc_final_path_bidir(
meetpointA, meetpointB, closed_set_A, closed_set_B)
return rx, ry
# takes both set and meeting nodes and calculate optimal path
def calc_final_path_bidir(self, n1, n2, setA, setB):
rxA, ryA = self.calc_final_path(n1, setA)
rxB, ryB = self.calc_final_path(n2, setB)
rxA.reverse()
ryA.reverse()
rx = rxA + rxB
ry = ryA + ryB
return rx, ry
def calc_final_path(self, ngoal, closedset):
# generate final course
rx, ry = [self.calc_grid_position(ngoal.x, self.minx)], [
self.calc_grid_position(ngoal.y, self.miny)]
n = closedset[ngoal.pind]
while n is not None:
rx.append(self.calc_grid_position(n.x, self.minx))
ry.append(self.calc_grid_position(n.y, self.miny))
n = n.parent
return rx, ry
def calc_grid_position(self, index, minp):
"""
calc grid position
:param index:
:param minp:
:return:
"""
pos = index * self.reso + minp
return pos
def calc_xyindex(self, position, min_pos):
return round((position - min_pos) / self.reso)
def calc_grid_index(self, node):
return (node.y - self.miny) * self.xwidth + (node.x - self.minx)
def verify_node(self, node):
px = self.calc_grid_position(node.x, self.minx)
py = self.calc_grid_position(node.y, self.miny)
if px < self.minx:
return False
elif py < self.miny:
return False
elif px >= self.maxx:
return False
elif py >= self.maxy:
return False
# collision check
if self.obmap[node.x][node.y]:
return False
return True
def calc_obstacle_map(self, ox, oy):
self.minx = round(min(ox))
self.miny = round(min(oy))
self.maxx = round(max(ox))
self.maxy = round(max(oy))
print("minx:", self.minx)
print("miny:", self.miny)
print("maxx:", self.maxx)
print("maxy:", self.maxy)
self.xwidth = round((self.maxx - self.minx) / self.reso)
self.ywidth = round((self.maxy - self.miny) / self.reso)
print("xwidth:", self.xwidth)
print("ywidth:", self.ywidth)
# obstacle map generation
self.obmap = [[False for _ in range(self.ywidth)]
for _ in range(self.xwidth)]
for ix in range(self.xwidth):
x = self.calc_grid_position(ix, self.minx)
for iy in range(self.ywidth):
y = self.calc_grid_position(iy, self.miny)
for iox, ioy in zip(ox, oy):
d = math.hypot(iox - x, ioy - y)
if d <= self.rr:
self.obmap[ix][iy] = True
break
@staticmethod
def get_motion_model():
# dx, dy, cost
motion = [[1, 0, 1],
[0, 1, 1],
[-1, 0, 1],
[0, -1, 1],
[-1, -1, math.sqrt(2)],
[-1, 1, math.sqrt(2)],
[1, -1, math.sqrt(2)],
[1, 1, math.sqrt(2)]]
return motion
def main():
print(__file__ + " start!!")
# start and goal position
sx = 10.0 # [m]
sy = 10.0 # [m]
gx = 50.0 # [m]
gy = 50.0 # [m]
grid_size = 2.0 # [m]
robot_radius = 1.0 # [m]
# set obstacle positions
ox, oy = [], []
for i in range(-10, 60):
ox.append(i)
oy.append(-10.0)
for i in range(-10, 60):
ox.append(60.0)
oy.append(i)
for i in range(-10, 61):
ox.append(i)
oy.append(60.0)
for i in range(-10, 61):
ox.append(-10.0)
oy.append(i)
for i in range(-10, 40):
ox.append(20.0)
oy.append(i)
for i in range(0, 40):
ox.append(40.0)
oy.append(60.0 - i)
if show_animation: # pragma: no cover
plt.plot(ox, oy, ".k")
plt.plot(sx, sy, "og")
plt.plot(gx, gy, "ob")
plt.grid(True)
plt.axis("equal")
bi_bfs = BidirectionalBreadthFirstSearchPlanner(ox, oy, grid_size, robot_radius)
rx, ry = bi_bfs.planning(sx, sy, gx, gy)
if show_animation: # pragma: no cover
plt.plot(rx, ry, "-r")
plt.pause(0.01)
plt.show()
if __name__ == '__main__':
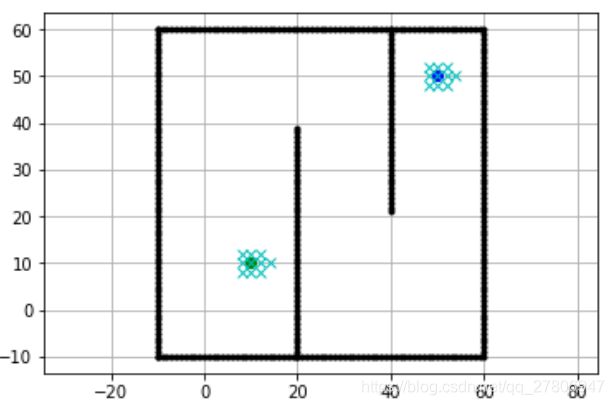
main()其栅格地图如下图所示:
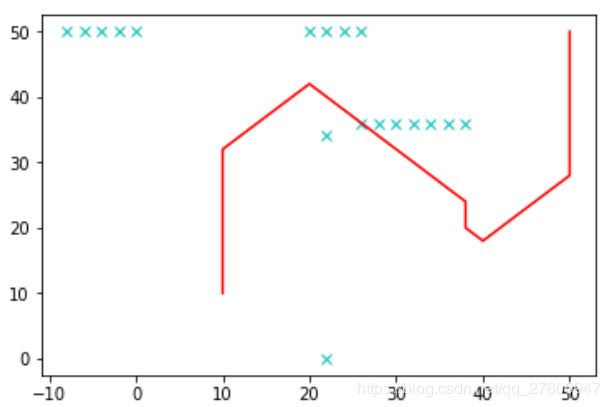
其最终搜索的路径如下图所示: