LeetCode选集:广度优先搜索&Dijkstra算法
文章目录
- 127.单词接龙
- 题目描述
- 思路
- 代码
- 199.二叉树的右视图
- 题目描述
- 思路
- 代码
- 417.太平洋大西洋水流问题
- 题目描述
- 思路
- 代码
- 542.01矩阵
- 题目描述
- 思路
- 代码
- 743.网络延迟时间
- 题目描述
- 思路
- 代码
- 752.打开转盘锁
- 题目描述
- 思路
- 代码
- 863. 二叉树中所有距离为 K 的结点
- 题目描述
- 思路
- 代码
127.单词接龙
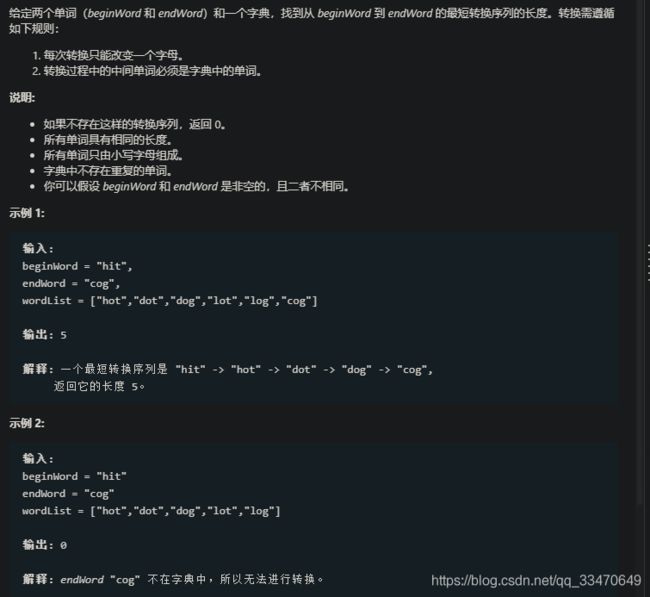
题目描述
思路
广度优先搜索
初始节点:beginWord
边:若y属于wordList,且x与y只相差一个字母,则称x、y间有边
终止:找到endWord
代码
int ladderLength(string beginWord, string endWord, vector<string> &wordList)
{
if (endWord == beginWord)
{
return 1;
}
unordered_set<string>wordSet(wordList.begin(), wordList.end());
queue<string>q{ {beginWord} };
int result = 1;
while (!q.empty())
{
result++;
for (int k = q.size(); k >= 1; k--)
{
const auto &s = q.front();
for (int m = 1; m <= s.size(); m++)
{
string tmp = s;
for (char c = 'a'; c <= 'z'; c++)
{
tmp[m - 1] = c;
if (wordSet.count(tmp) != 0 && tmp != s)
{
if (tmp == endWord)
{
return result;
}
q.push(tmp);
wordSet.erase(tmp);
}
}
}
q.pop();
}
}
return 0;
}
199.二叉树的右视图
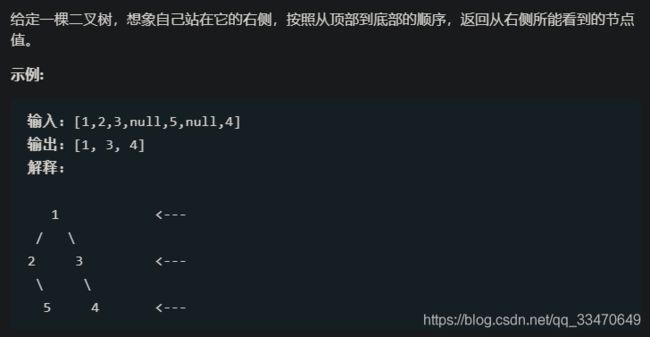
题目描述
思路
广度优先搜索
初始节点:根节点
边:与二叉树的边相同
终止:找到所有节点
代码
vector<int> rightSideView(TreeNode *root)
{
if (root == nullptr)
{
return {};
}
queue<TreeNode*>q{ {root} };
vector<int>result;
while (!q.empty())
{
result.push_back(q.back()->val);
for (int n = q.size(); n >= 1; n--)
{
const auto &x = q.front();
if (x->left != nullptr)
{
q.push(x->left);
}
if (x->right != nullptr)
{
q.push(x->right);
}
q.pop();
}
}
return result;
}
417.太平洋大西洋水流问题
题目描述
思路
广度优先搜索
初始节点:位于大西洋或太平洋的边缘的节点
边:若x、y相邻,且有x.val≤y.val,认为存在x到y的有向边
终止:找到所有节点
分别对大西洋和太平洋作搜索,最后取找到的节点的交集即可
代码
vector<pair<int, int>>dxys = { pair<int, int>(-1, 0), pair<int, int>(1, 0), pair<int, int>(0, -1), pair<int, int>(0, 1) };
int n_Row, n_Col;
void Find(const vector<vector<int>> &matrix, deque<pair<int, int>> &q, vector<vector<bool>> &findedList)
{
while (!q.empty())
{
for (int n = q.size(); n >= 1; n--)
{
const auto &x = q.front();
for (const auto &dxy : dxys)
{
int row = x.first + dxy.first, col = x.second + dxy.second;
if (row<1 || row>n_Row || col<1 || col>n_Col)
{
continue;
}
if (!findedList[row - 1][col - 1] && matrix[row - 1][col - 1] >= matrix[x.first - 1][x.second - 1])
{
findedList[row - 1][col - 1] = true;
q.emplace_back(row, col);
}
}
q.pop_front();
}
}
}
vector<vector<int>> pacificAtlantic(vector<vector<int>> &matrix)
{
n_Row = matrix.size();
if (n_Row == 0)
{
return {};
}
n_Col = matrix[0].size();
deque<pair<int, int>>q1, q2;
vector<vector<bool>>findedList1(n_Row, vector<bool>(n_Col, false));
auto findedList2 = findedList1;
for (int row = 1; row <= n_Row; row++)
{
q1.emplace_back(row, 1);
q2.emplace_back(row, n_Col);
findedList1[row - 1][0] = 1;
findedList2[row - 1][n_Col - 1] = 1;
}
for (int col = 1; col <= n_Col; col++)
{
q1.emplace_back(1, col);
q2.emplace_back(n_Row, col);
findedList1[0][col - 1] = 1;
findedList2[n_Row - 1][col - 1] = 1;
}
Find(matrix, q1, findedList1);
Find(matrix, q2, findedList2);
vector<vector<int>>result;
for (int row = 1; row <= n_Row; row++)
{
for (int col = 1; col <= n_Col; col++)
{
if (findedList1[row - 1][col - 1] && findedList2[row - 1][col - 1])
{
result.push_back({ row - 1, col - 1 });
}
}
}
return result;
}
542.01矩阵
题目描述
思路
广度优先搜索
初始节点:所有值为0的节点
边:存在于所有相邻节点间
终止:找到所有节点
代码
vector<vector<int>> updateMatrix(vector<vector<int>> &matrix)
{
int n_Row = matrix.size(), n_Col = matrix[0].size();
vector<vector<int>>result(n_Row, vector<int>(n_Col, -1));
vector<pair<int, int>>dxys = { pair<int, int>(-1, 0), pair<int, int>(1, 0), pair<int, int>(0, -1), pair<int, int>(0, 1) };
queue<pair<int, int>>q;
for (int row = 1; row <= n_Row; row++)
{
for (int col = 1; col <= n_Col; col++)
{
if (matrix[row - 1][col - 1] == 0)
{
result[row - 1][col - 1] = 0;
q.emplace(row, col);
}
}
}
int count = 0;
while (!q.empty())
{
count++;
for (int n = q.size(); n >= 1; n--)
{
const auto &x = q.front();
for (const auto &dxy : dxys)
{
int row = dxy.first + x.first, col = dxy.second + x.second;
if (row >= 1 && row <= n_Row && col >= 1 && col <= n_Col)
{
if (result[row - 1][col - 1] != -1)
{
continue;
}
result[row - 1][col - 1] = count;
q.emplace(row, col);
}
}
q.pop();
}
}
return result;
}
743.网络延迟时间
题目描述
思路
Dijkstra算法与广度优先搜索类似,在广度优先搜索中由于各边权重相同,先发现的节点也必然是距离最短的节点,因此可以使用简单的先进先出队列,节点的距离在加入队列时就已确定;在Dijkstra算法中,需要使用优先队列,只有当节点从队列中弹出时,其距离才被确定,而队列中的其它节点的距离可能被更新。
优先队列可以有不同的实现,当图的边较多时,可以直接使用数组实现,每次遍历找出最小距离节点,复杂度O(V²);当图边较少时,可以使用堆实现,复杂度O(VlgV),另外注意根据边更新堆中节点的距离时有额外的复杂度O(ElgV)
代码
int networkDelayTime(vector<vector<int>> ×, int N, int K)
{
vector<vector<pair<int, int>>>linkList(N, vector<pair<int, int>>{});
vector<int>timeList(N, INT32_MAX);
unordered_set<int>findedSet;
timeList[K - 1] = 0;
for (const auto &time : times)
{
linkList[time[0] - 1].emplace_back(time[1], time[2]);
}
while (true)
{
int time = INT32_MAX, order = 0;
for (int n = 1; n <= N; n++)
{
if (timeList[n - 1] < time&&findedSet.count(n) == 0)
{
time = timeList[n - 1];
order = n;
}
}
if (time == INT32_MAX)
{
break;
}
if (findedSet.size() == N - 1)
{
return time;
}
findedSet.insert(order);
for (const auto &x : linkList[order - 1])
{
timeList[x.first - 1] = min(timeList[x.first - 1], timeList[order - 1] + x.second);
}
}
return -1;
}
752.打开转盘锁
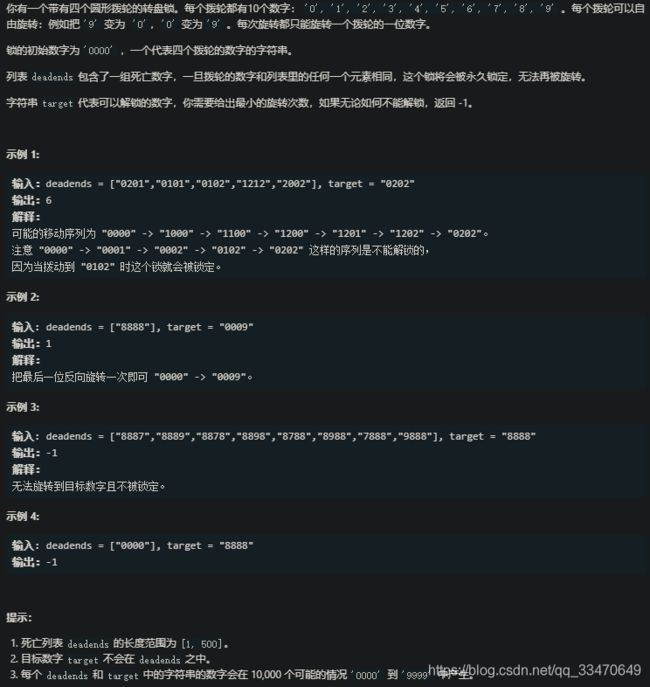
题目描述
思路
广度优先搜索
初始节点:“0000”
边:若x旋转一位数字得到y,称x、y之间存在边
终止:找到target
有一个死亡数字的概念,若从队列中弹出的x为死亡数字,则不使用它来搜索邻接节点
代码
int openLock(vector<string> &deadends, string target)
{
if (target == "0000")
{
return 0;
}
unordered_set<string>deadSet(deadends.begin(), deadends.end());
unordered_set<string>findedSet{ "0000" };
queue<string>q{ {"0000"} };
int result = 0;
while (!q.empty())
{
result++;
for (int n = q.size(); n >= 1; n--)
{
string s = q.front();
q.pop();
if (deadSet.count(s) != 0)
{
continue;
}
for (int m = 1; m <= 4; m++)
{
for (int n = -1; n <= 1; n += 2)
{
string tmp = s;
if (tmp[m - 1] == '0'&&n == -1)
{
tmp[m - 1] = '9';
}
else if (tmp[m - 1] == '9'&&n == 1)
{
tmp[m - 1] = '0';
}
else
{
tmp[m - 1] += n;
}
if (tmp == target)
{
return result;
}
if (findedSet.count(tmp) != 0)
{
continue;
}
q.push(tmp);
findedSet.insert(tmp);
}
}
}
}
return -1;
}
863. 二叉树中所有距离为 K 的结点
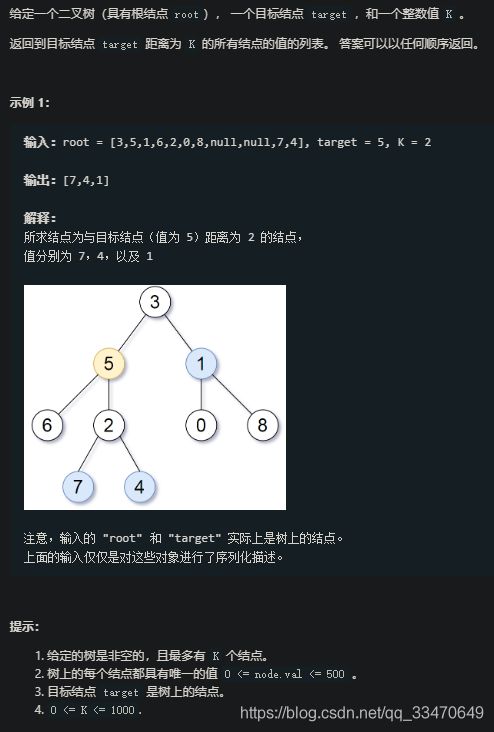
题目描述
思路
广度优先搜索
初始节点:target
边:与二叉树相同
终止:所有距离为K的节点
仅靠二叉树的左右节点指针无法给出所有的边,因此需要额外进行一次广度优先搜索建立邻接链表
代码
void InitLinkList(vector<vector<int>> &linkList, TreeNode *root)
{
queue<TreeNode*>q{ {root} };
while (!q.empty())
{
const auto &x = q.front();
if (x->left)
{
q.push(x->left);
linkList[x->val].push_back(x->left->val);
linkList[x->left->val].push_back(x->val);
}
if (x->right)
{
q.push(x->right);
linkList[x->val].push_back(x->right->val);
linkList[x->right->val].push_back(x->val);
}
q.pop();
}
}
vector<int> distanceK(TreeNode *root, TreeNode *target, int K)
{
if (K == 0)
{
return { target->val };
}
vector<vector<int>>linkList(501, vector<int>{});
InitLinkList(linkList, root);
vector<int>findedList(501, 0);
findedList[target->val] = 1;
queue<int>q{ {target->val} };
vector<int>result;
for (int distance = 1; distance <= K; distance++)
{
for (int n = q.size(); n >= 1; n--)
{
const auto &x = q.front();
for (const auto &node : linkList[x])
{
if (findedList[node] == 0)
{
findedList[node] = 1;
q.push(node);
if (distance == K)
{
result.push_back(node);
}
}
}
q.pop();
}
}
return result;
}