JAVA数据结构——利用图的广度优先遍历搜索算法确定无向连通图的连通分量
分析:
如果这个无向图是非连通图的时候,从图的一个顶点没法访问这个图的所有顶点,只能访问包含该顶点的连通分量中的所有顶点。所以从无向图的每个连通分量中的一个顶点开始遍历图,则可求得无向图的所有连同分量。
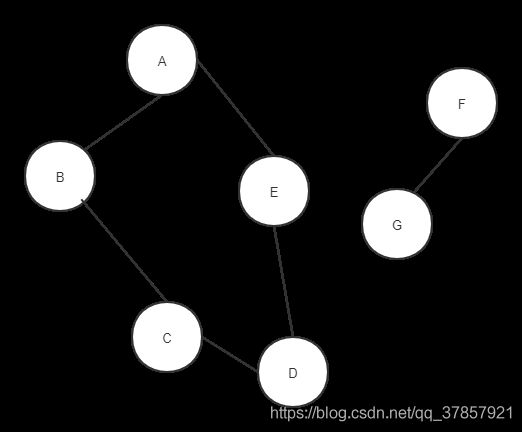
如图则是非连通的无向图,我们只需要从第一个和第二个连通分量进行遍历即可,先了解一下基础设想。
从1-2-...n,我们可以把这个思路无限制扩大下去,实现若干个非连通图如何实现。
我们采用广度优先遍历搜索算法来实现这个功能。
广度优先遍历搜索(BFS):
广度优先遍历,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
已知图G=(V,E)和一个源顶点s,宽度优先搜索以一种系统的方式探寻G的边,从而“发现”s所能到达的所有顶点,并计算s到所有这些顶点的距离(最少边数),该算法同时能生成一棵根为s且包括所有可达顶点的宽度优先树。对从s可达的任意顶点v,宽度优先树中从s到v的路径对应于图G中从s到v的最短路径,即包含最小边数的路径。该算法对有向图和无向图同样适用。
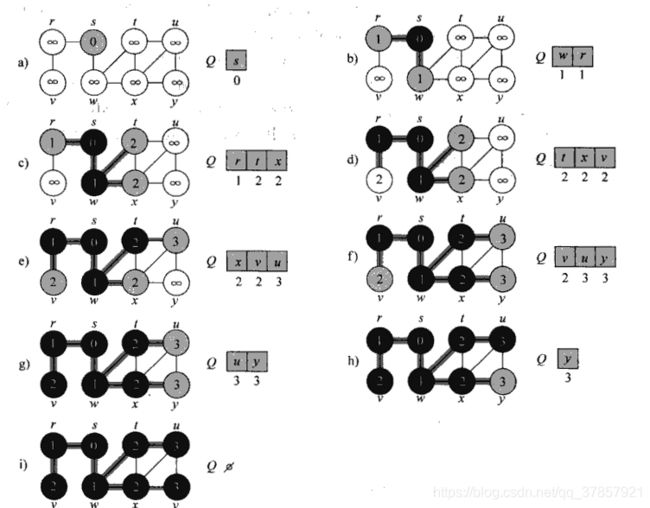
之所以称之为宽度优先算法,是因为算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展,就是说,算法首先搜索和s距离为k的所有顶点,然后再去搜索和S距离为k+l的其他顶点。
为了保持搜索的轨迹,宽度优先搜索为每个顶点着色:白色、灰色或黑色。算法开始前所有顶点都是白色,随着搜索的进行,各顶点会逐渐变成灰色,然后成为黑色。在搜索中第一次碰到一顶点时,我们说该顶点被发现,此时该顶点变为非白色顶点。因此,灰色和黑色顶点都已被发现,但是,宽度优先搜索算法对它们加以区分以保证搜索以宽度优先的方式执行。若(u,v)∈E且顶点u为黑色,那么顶点v要么是灰色,要么是黑色,就是说,所有和黑色顶点邻接的顶点都已被发现。灰色顶点可以与一些白色顶点相邻接,它们代表着已找到和未找到顶点之间的边界。
在宽度优先搜索过程中建立了一棵宽度优先树,起始时只包含根节点,即源顶点s.在扫描已发现顶点u的邻接表的过程中每发现一个白色顶点v,该顶点v及边(u,v)就被添加到树中。在宽度优先树中,我们称结点u 是结点v的先辈或父母结点。因为一个结点至多只能被发现一次,因此它最多只能有--个父母结点。相对根结点来说祖先和后裔关系的定义和通常一样:如果u处于树中从根s到结点v的路径中,那么u称为v的祖先,v是u的后裔。
代码实现利用广度优先遍历搜索确定无向图的连通分量:
1. 图类型:
package com.usts.edu.graphic;
// 图的种类 有向图、有向网、无向图、无向网
public enum GraphKind {
UDG, // 无向图(UnDirected Graph)
DG, // 有向图(Directed Graph)
UDN, // 无向网(UnDirected Network)
DN; // 有向网(Directed Network)
}
2. 图的接口
package com.usts.edu.graphic;
//图的接口
public interface IGraph {
void createGraph();//创建一个图
int getVexNum(); // 返回顶点数
int getArcNum();// 返回边数
Object getVex(int v) throws Exception;// 返回v表示结点的值, 0 <= v < vexNum
int locateVex(Object vex);// 给定顶点的值vex,返回其在图中的位置,如果图中不包含此顶点,则返回-1
int firstAdjVex(int v) throws Exception; // 返回v的第一个邻接点,若v没有邻接点,则返回-1,其中0≤v3. 创建图:
package com.usts.edu.graphic;
import java.util.Scanner;
public class MGraph implements IGraph {
public final static int INFINITY = Integer.MAX_VALUE;
private GraphKind kind;
private int vexNum, arcNum;
private Object[] vexs;
private int[][] arcs;
public MGraph() {
this(null, 0, 0, null, null);
}
public MGraph(GraphKind kind, int vexNum, int arcNum, Object[] vexs,
int[][] arcs) {
this.kind = kind;
this.vexNum = vexNum;
this.arcNum = arcNum;
this.vexs = vexs;
this.arcs = arcs;
}
public void createGraph() {
Scanner sc = new Scanner(System.in);
System.out.println("请输入图的类型");
GraphKind kind = GraphKind.valueOf(sc.next());
switch (kind) {
case UDG:
createUDG();
return;
case DG:
createDG();
return;
case UDN:
createUDN();
return;
case DN:
createDN();
return;
}
}
private void createUDG() {
};
private void createDG() {
};
private void createUDN() {
Scanner sc = new Scanner(System.in);
vexNum = sc.nextInt();
arcNum = sc.nextInt();
vexs = new Object[vexNum];
for (int v = 0; v < vexNum; v++)
vexs[v] = sc.next();
arcs = new int[vexNum][vexNum];
for (int v = 0; v < vexNum; v++)
for (int u = 0; u < vexNum; u++)
arcs[v][u] = INFINITY;
for (int k = 0; k < arcNum; k++) {
int v = locateVex(sc.next());
int u = locateVex(sc.next());
arcs[v][u] = arcs[u][v] = sc.nextInt();
}
}
private void createDN() {
Scanner sc = new Scanner(System.in);
vexNum = sc.nextInt();
arcNum = sc.nextInt();
vexs = new Object[vexNum];
for (int v = 0; v < vexNum; v++)
vexs[v] = sc.next();
arcs = new int[vexNum][vexNum];
for (int v = 0; v < vexNum; v++)
for (int u = 0; u < vexNum; u++)
arcs[v][u] = INFINITY;
for (int k = 0; k < arcNum; k++) {
int v = locateVex(sc.next());
int u = locateVex(sc.next());
arcs[v][u] = sc.nextInt();
}
}
public int getVexNum() {
return vexNum;
}
public int getArcNum() {
return arcNum;
}
public int locateVex(Object vex) {
for (int v = 0; v < vexNum; v++)
if (vexs[v].equals(vex))
return v;
return -1;
}
public Object getVex(int v) throws Exception {
if (v < 0 && v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
return vexs[v];
}
public int firstAdjVex(int v) throws Exception {
if (v < 0 && v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
for (int j = 0; j < vexNum; j++)
if (arcs[v][j] != 0 && arcs[v][j] < INFINITY)
return j;
return -1;
}
public int nextAdjVex(int v, int w) throws Exception {
if (v < 0 && v >= vexNum)
throw new Exception("第" + v + "个顶点不存在!");
for (int j = w + 1; j < vexNum; j++)
if (arcs[v][j] != 0 && arcs[v][j] < INFINITY)
return j;
return -1;
}
public GraphKind getKind() {
return kind;
}
public int[][] getArcs() {
return arcs;
}
public Object[] getVexs() {
return vexs;
}
public void setArcNum(int arcNum) {
this.arcNum = arcNum;
}
public void setArcs(int[][] arcs) {
this.arcs = arcs;
}
public void setKind(GraphKind kind) {
this.kind = kind;
}
public void setVexNum(int vexNum) {
this.vexNum = vexNum;
}
public void setVexs(Object[] vexs) {
this.vexs = vexs;
}
}
4. 实现搜索:
package com.usts.edu.graphic;
import com.usts.edu.Queue.LinkQueue;
/**
* Created by Guanzhong Hu
* Date :2020/3/30
* Description :
* Version :1.0
*/
public class GDSeach {
public final static int INFINITY = Integer.MAX_VALUE;
public static void CC_BFS(IGraph G) throws Exception {
boolean[] visited = new boolean[G.getVexNum()];
for (int v = 0; v < G.getVexNum(); v++)
visited[v] = false;
LinkQueue Q = new LinkQueue();
LinkQueue P = new LinkQueue();
int i = 0;
for (int v = 0; v < G.getVexNum(); v++) {
P.clear();
if (!visited[v]) {
visited[v] = true;
P.offer(G.getVex(v));
Q.offer(v);
while (!Q.isEmpty()) {
int u = (Integer) Q.poll();
for (int w = G.firstAdjVex(u); w >= 0; w = G.nextAdjVex(u,
w)) {
if (!visited[w]) {
visited[w] = true;
P.offer(G.getVex(w));
Q.offer(w);
}
}
}
System.out.println("图的第" + ++i + "个连通分量为:");
while (!P.isEmpty())
System.out.print(P.poll().toString() + " ");
System.out.println();
}
}
}
public static void main(String[] args) throws Exception {
Object vexs[] = { "A", "B", "C", "D", "E", "F", "G" };
int[][] arcs = { { 0, 1, INFINITY, 1, INFINITY, INFINITY, INFINITY },
{ 1, 0, 1, INFINITY, INFINITY, INFINITY, INFINITY },
{ INFINITY, 1, 0, 1, INFINITY, INFINITY, INFINITY },
{ 1, INFINITY, 1, 0, INFINITY, INFINITY, INFINITY },
{ INFINITY, INFINITY, INFINITY, INFINITY, 0, 1, INFINITY },
{ INFINITY, INFINITY, INFINITY, INFINITY, 1, 0, 1 },
{ INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, 1, 0 }, };
MGraph G = new MGraph(GraphKind.UDG, 7, 6, vexs, arcs);
CC_BFS(G);
}
}
无向图的连通分量搜索是一种广度优先遍历的应用,当然还有如Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
源码地址:https://gitee.com/jockhome/data_structure