栈和队列(一)
栈和队列是两种重要的线性结构。从数据结构来看,栈和队列也是线性表,其特殊性在于栈和队列的基本操作是线性表操作的子集,它们是操作受限的线性表,因此,可称为限定性的数据结构。但从数据类型角度看,它们是和线性表不相同的两类重要的抽象数据类型。
1.1栈和队列的定义和特点
1.1.1栈的定义和特点
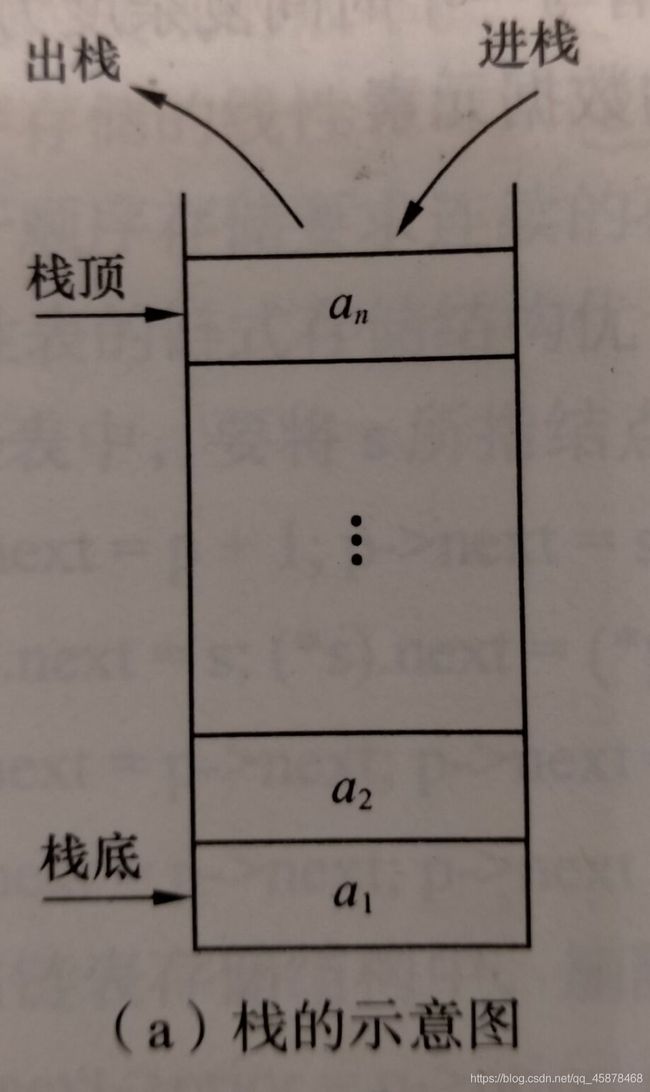
- 栈(stack)是限定仅在表尾进行插入或删除操作的线性表。
- 对栈来说,表尾端有其特殊含义,称为栈顶(top),相应地,表头端称为栈底(bottom)。
- 不含元素的空表称为空栈。
- 假设栈S=(a1,a2,...,an),则a1为栈底元素,an为栈顶元素。栈中元素按a1,a2,...,an的次序进栈,退栈的第一个元素应为栈顶元素。
- 栈的修改是按后进先出的原则进行的,栈又称为后进先出(Last In First Out,LIFO)的线性表。如果需要按照保存数据时相反的顺序来使用数据,则可以利用栈来实现。
- 相关案例有,数制的转换,括号匹配的检验,表达式求值等。
1.1.2队列的定义和特点
- 和栈相反,队列(queue)是一种先进先出(First In First Out,FIFO)的线性表。它只允许在表的一端进行插入,而在另一端删除元素。这和日常生活中的排队是一致的,最早进入队列的元素最早离开。
- 在队列中,允许插入的一端称为队尾(rear),允许删除的一端则称为队头(front)。
- 假设队列为q=(a1,a2,...,an),那么,a1就是队头元素,an则是队尾元素。队列中的元素是按照a1,a2,...,an的顺序进入的,退出队列也只能按照这个次序依次退出。
- 相关案例有舞伴问题等。
不论是借助栈还是队列来解决问题,最基本的操作都是“入”和“出”。对于栈,在栈顶插入元素的操作称为“入栈”,删除栈顶元素的操作称为“出栈”;对于队列,在队尾插入元素的操作称为“入队”,在队头删除元素的操作称作“出队”。和线性表一样,栈和队列的存储结构也包括顺序和链式两种。
1.2栈的表示和操作的实现
1.2.1栈的类型定义
栈的基本操作除了入栈和出栈外,还有栈的初始化、栈空的判定以及取栈顶元素等。下面给出栈的抽象数据类型定义:
和线性表类似,栈也有两种存储表示方法,分别称为顺序栈和链栈。
1.2.2顺序栈的表示和实现
顺序栈是利用顺序存储结构实现的栈,即利用一组地址连续的存储单元依次存放自栈底到栈底的数据元素,同时附设指针top指示栈顶元素在顺序栈中的位置。通常习惯的做法是:以top=0表示空栈,另设指针base指示栈底元素在顺序栈中的位置。当top和base的值相等时,表示空栈。
//- - - - -顺序栈的存储结构- - - - -
#define MAXSIZE 100 //顺序栈存储空间的初始分配量
typedef struct
{
SElemType *base; //栈底指针
SElemType *top; //栈顶指针
int stacksize; //栈可用的最大容量
}SqStack;- base为栈底指针,初始化完成后,栈底指针base始终指向栈底的位置,若base的值为NULL,则表明栈结构不存在。top为栈顶指针,其初值指向栈底。每当插入新的栈顶元素时,指针top赠1;删除栈顶元素时,指针top减1。栈空时,top和base的值相等,都指向栈底;栈非空时,top始终指向栈顶元素的上一个位置。
- stacksize指示栈可使用的最大容量。
顺序栈中数据元素和栈指针之间的对应关系:
顺序栈的插入和删除只在栈顶进行,下面给出顺序栈的初始化操作的实现:
1.初始化
顺序栈的初始化操作就是为顺序栈动态分配一个预定义大小的数组空间。
Status InitStack(SqStack &S)
{//构造一个空栈S
S.base=new SElemType[MAXSIZE]; //为顺序栈动态分配一个最大容量为MAXSIZE的数组空间
if(!S.base) exit(OVERFLOW); //存储分配失败
S.top=S.base; //top初始为base,空栈
S.stacksize=MAXSIZE; //stacksize置为栈的最大容量MAXSIZE
return OK;
}2.入栈
入栈操作是指在栈顶插入一个新的元素。
Status Push(SqStack &S, SElemType e)
{//插入元素e为新的栈顶元素
if(S.top-S.base==S.stacksize) return ERROR; //栈满
*S.top++=e; //元素e压入栈顶,栈顶指针加1
return OK;
}3.出栈
出栈操作时是将栈顶元素删除。
Status Pop(SqStack &S,SElemType &e)
{//删除S的栈顶元素,用e返回其值
if(S.top==S.base) return ERROR; //栈空
e=*--S.top; //栈顶指针减1,将栈顶元素赋给e
return OK;
}4.取栈顶元素
当栈非空时,此操作返回当前栈顶元素的值,栈顶指针保持不变。
SElemType GetTop(SqStack S)
{//返回S的栈顶元素,不修改栈顶指针
if(S.top!=S.base) //栈非空
return *(S.top-1); //返回栈顶元素的值,栈顶指针不变
}1.2.3链栈的表示和实现
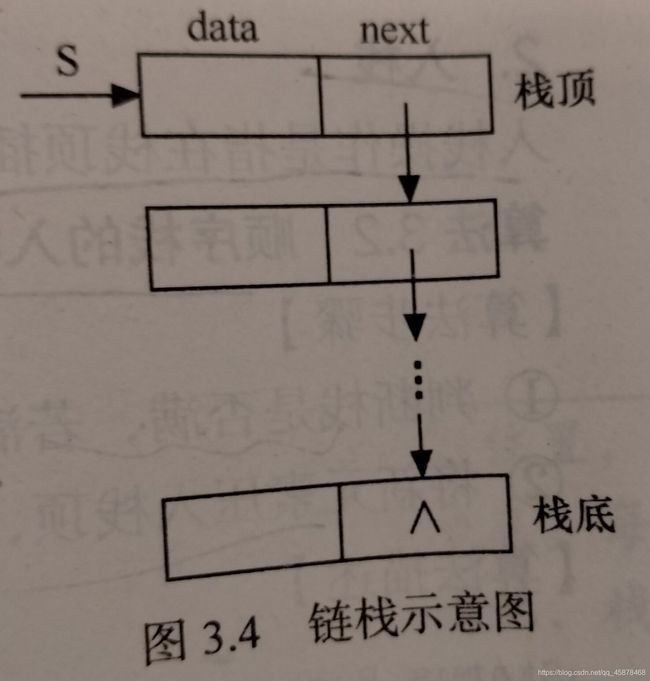
链栈是指采用链式存储结构实现的栈。通常链栈用单链表来表示,链栈的结点结构与单链表的结构相同,在此用StackNode表示:
//- - - - -链栈的存储结构- - - - -
typedef struct StackNode
{
ElemType data;
struct StackNode *next;
}StackNode,*LinkStack;
栈的主要操作是在栈顶插入和删除,显然以链表的头部作为栈顶是最方便的,而且没必要像单链表那样为了操作方便附加个头结点。下面是链栈部分操作的实现:
1.初始化
链栈的初始化操作就是构造一个空栈,因为没必要设头结点,所以直接将栈顶指针置空即可。
Status InitStack(LinkStack &S)
{//构造一个空栈S,栈顶指针置空
S=NULL;
return OK;
}2.入栈
链栈在入栈前不需要判断栈是否满,只需要为入栈元素动态分配一个结点空间。
Status Push(LinkStack &S, SElemType e)
{//在栈顶插入元素e
p=new StackNode; //生成新结点
p->data=e; //将新结点数据域置为e
p->next=S; //将新结点插入栈顶
S=p; //修改栈顶指针为p
return OK;
}3.出栈
和顺序栈一样,链栈在出栈前也需要判断栈是否为空,不同的是,链栈在出栈后需要释放出栈元素的栈顶空间。
Status Pop(LinkStack &S,SElemType &e)
{//删除S的栈顶元素,用e返回其值
if(S==NULL) return ERROR; //栈空
e=S->data; //将栈顶元素赋给e
p=S; //用p临时保存栈顶元素空间,以备释放
S=S->next; //修改栈顶指针
delete p; //释放原栈顶元素的空间
return OK;
}4.取栈顶元素
与顺序栈一样,当栈非空时,此操作返回当前栈顶元素的值,栈顶指针S保持不变。
SElemType GetTop(LinkStack S)
{//返回S的栈顶元素,不修改栈顶指针
if(S!=NULL) //栈非空
return S->data; //返回栈顶元素的值,栈顶指针不变
}