字典树（Trie）和题

基本操作

如果我们需要统计、排序或者保存大量字符串，就可以用到字典树。

举个例子，这里有一个集合，包含下面2个单词。

apply
buy

查找

如果要判断这个集合中是否有某个单词，我们可以把这2个单词建成下图表示的树：

如果要判断这个集合中有没有“apply”这个词，我们可以从根结点开始向下逐层找。可以看到，树的第2层有“apply”的第1个字母、第3层有它的第2个字母。一直到第6层，每一层都有对应的字母，那么我们可以说，“apply”这个词在这个集合中。

如果我们要查找的是“app”这个词呢？可以看到，按照上面的查找方式，我们会认为“app”这个词也在上面 的集合中——这就出问题了。

为了避免这样的问题发生，我们可以在树中标记出每个单词的最后一个字母（图中两个单词的最后一个字母的结点都画成了黑白的结节）。我们再来找“app”这个词。虽然树中仍有“app”这个序列，但是结点“p”没有标记，即，字母“p”不是某个字符串的最后一个字母。所以我们可以说，原集合中是没有“app”这个词的。如果原集合中有“app”这个词，那么在路径“app”上的第二个“p”结点应该是黑白的才对。

添加

如果要向原集合添加下列新单词，要怎么做呢？

apex
but
car

“apex”与原有的“apple”有着相同的前缀“ap”，不妨让它们共用相同的结点；而“car”的前缀是新出现的，就不得不为它创建全新结点了：

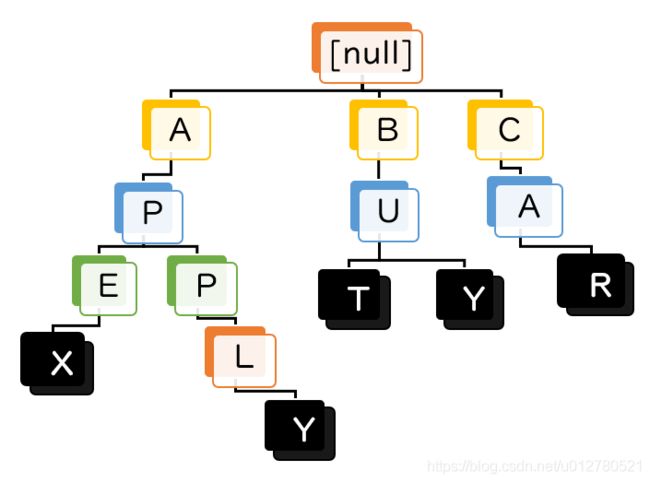
同样地，为新加入的每个单词的最后一个字母做标记。这样一来，我们仍然能用上述方法准确地查找字符串。

统计

字典树也可以用来统计字符串的出现次数。

树中的每一个带有标记的结点都对应一种字符串，而且这种对应关系是 一一对应 的，不会有多个有标记结点对应相同的字符串，也不会有一个有标记结点对应多个不同的字符串。 我们可以在带有标记结点中添加一个计数器记录这个字符串的出现次数。每一次添加字符串时，如果该字符串已经存在了，就为它的标记结点中的计数器加一。统计字符串出现次数时，只要看有标记结点中的计数器就行了。

优势

上一节中，我们研究的字符串集合是

apex
apply
but
buy
car

如果我们不使用字典树，直接查找“apply”，那我们会将“apply”与集合中的各个字符串的逐个字符依次比较。在这个例子中，由于“ap”同时是“apex”与“apply”的前缀，我们会将公共前缀序列“ap”重复比较两次。如果使用字典树来查找，我们就可以避免重复地比较相同的前缀，只要沿着“ap”序列对应的路径往下走就可以了。

概括起来，它的优点是利用字符串的公共前缀来减少查询时间，最大限度地减少重复的字符串比较。

字典树因此也叫做“前缀树”。

缺点

字符串长度过大或者字符集过大（即，字符种类过多）时，就不宜用字典树了。

如果字符串长度过大，字典树就会很深，其查找的效率会降低，而且会占用很多空间。这种情况下我们可以改用 散列表（Hash table）。

如果字符种类很多（比如说，输入中文文章），字典树的每一层都会特别宽，也会占用很多空间。

常见应用

将字符串组按字典序排序

建立字典树，将每个结点的子结点按字典序排序，然后先序遍历树并输出即可。

如果用基于数组的邻接表来保存每个结点的子结点，并将字符按照字典序映射到数组下标，那么每个结点的子结点就自然是有序的了。

代码如下：
// 省略了包含头文件和命名空间的代码。
// islower 和 isupper 函数用于判断一个字符是不是小写字母或者大写字母，在头文件 cctype 或者 ctype.h 中

struct Node
{
	int frequency = 0; // 以当前结点为结尾的单词个数。若不是结尾，值为 0 
	char data = 0; // 存储该结点的字符
	int children[26]; // 邻接表。将 'a'或者 'A'映射到下标 0

	Node()
	{
		memset(children, -1, sizeof(children));// 将邻接表全部初始化为 -1
	}
};

Node tree[1000]; // tree[0] 作为根结点，其中不存字符。
string word;
int pos, num, cur, len, ch;

// 先序遍历树并输出
void rfprint(int pos = 0, string buf = string(""))
{
	if (tree[pos].data)
		buf += tree[pos].data;
	for (int i = tree[pos].frequency; i > 0; --i)
	{
		cout << buf;
		putchar('\n');
	}
	for (const int i : tree[pos].children)
		if (i > -1)
			rfprint(i, buf);
}

int main()
{
	while (cin >> word)
	{
		pos = 0; 
		len = word.size();
		for (auto i = 0; i < len; ++i)
		{
		    // 只选取字符串中的英文字母，并将全部字母变为小写
			if (isupper(word[i]))
				ch = word[i] - 'A';
			else if (islower(word[i]))
				ch = word[i] - 'a';
			else
				continue;
			if (tree[pos].children[ch] < 0)
				tree[pos].children[ch] = ++cur;
			pos = tree[pos].children[ch];
			tree[pos].data = word[i];
		}
		++tree[pos].frequency;
	}
	rfprint();
	return 0;
}

查找最长公共前缀

建立字典树，问题转化为求公共祖先数。

题

1

题目

题目来源：洛谷 P2580 于是他错误的点名开始了
【题目描述】
给出一个班级中的学生的名单及老师的点名过程。对于每一次点名，判断该次点名是否正确。


【输入格式】
第一行一个整数 $n$，表示学生人数。
之后 n 行每行一个字符串表示姓名，只含小写字母，没有重复姓名，长度不超过 $50$。
第 $(n+2)$ 行一个整数 $m$，表示点名次数。
之后 m 行每行一个字符串表示老师报的名字，只含小写字母，长度不超过 $50$。
$n\le 10000，m\le 100000$


【输出格式】
对于每次点名，输出一行。如果该名字正确且是第一次出现，输出“OK”，如果该名字错误，输出“WRONG”，如果该名字正确但不是第一次出现，输出“REPEAT”。（均不加引号）

分析

可以用字典树。也可以用散列表。

代码

#include 
#include 
#include 
#define INDEX(ch) (ch - 'a')

char in[51];
int tree[500003][26];
// 邻接表
// tree[0] 表示字典树根结点的邻接表。
// 字符 'a' 映射到下标 0
char leaf[500003];
// leaf[x] 记录 x 号结点是否为字符串的结尾，并记录这个字符串是否被访问过。
// 2 表示"已访问"。1 表示"未访问的结尾"。0 表示"不是结尾".

int main()
{
	int pos, cur = 0, len, t;
	scanf("%d", &t);
	getchar();
	while (t--)
	{
		scanf("%s", in);
		pos = 0;
		for (int j = 0; in[j]; ++j)
		{
			if (tree[pos][INDEX(in[j])] == 0)
				tree[pos][INDEX(in[j])] = ++cur;
			pos = tree[pos][INDEX(in[j])];
		}
		leaf[pos] = 1;
	}
	scanf("%d", &t);
	getchar();
	while (t--)
	{
		scanf("%s", in);
		len = strlen(in);
		pos = 0;
		for (int j = 0; j < len; ++j)
			if ((pos = tree[pos][INDEX(in[j])]) == 0)
				break;
		if (leaf[pos] == 1)
		{
			printf("OK\n");
			leaf[pos] = 2;
		}
		else
			printf(leaf[pos] ? "REPEAT\n" : "WRONG\n");
	}
	return 0;
}

2

题目

题目来源：ICPC SouthWestern Europe Regional Contest 2018
【题目描述】
填字游戏。有 $N$ 行 $M$ 列的表格，及两组字符串。甲组有 $A$ 个长度为 $N$ 的字符串，乙组有 $B$ 个长度为 $M$ 的字符串。
要在表格中填入上述字符串，每个格子中都要恰好填一个字符，使得表格中每一行字符串都是乙组中的字符串，同时每一列都是甲组中的字符串。
求所有可能的填入方式总数。


【输入格式】
前四个整数分别为 $N、A、M、B$。
之后的 $A$ 行，每行一个长度为 $N$ 的字符串，表示甲组的字符串。
之后的 $B$ 行，每行一个长度为 $M$ 的字符串，表示乙组的字符串。


【输入格式】
单行，一个整数。所有可能的填入方式总数。


【限制条件】
$N$ 与 $M$ 大于 $1$ 且小于 $5$。
$A$ 与 $B$ 之积不大于 $1008016$        // 即 $1004$ 的平方——编者著。
甲组字符串只能竖着填；乙组字符串只能横着填。
字符串只由 26 个小写字母组成。
出现在一组中的字符串不会出现在另一组中。


【样例输入】
3 4
4 5
war
are
yes
sat
says
area
test
ways
rest


【样例输出】
2


【样例说明】

分析

表格最大只有 16 格。可以考虑暴力搜索。
所有可能的填法有 $26^{16}$ 种，太多，所以要剪枝。
可以建立字典树。然后 DFS，逐格暴力填，每填一个字母，就利用字典树判断该填法是否可行，同时据此剪枝。
考虑到两组字符串不等价，应该建立两个字典树。

代码

#include 
#define sfor(i,n) for(int i=0;i
#define gch() ch=getchar()
#define V(s,c) vtree[s][c]
#define H(s,c) htree[s][c]
#define TREE_SIZE 500000  // 单棵树的结点总量
#define CHARSET 26 // 字符集大小
#define LEN 4  // 表格边长
int nro, nco, nvert, nhorz; //分别对应题目中的 n, m, a, b
long long res; // 记录结果
char mat[LEN][LEN];
int vtree[TREE_SIZE][CHARSET];  // 甲组的树的邻接表。vtree[0] 为根结点的邻接表。
int htree[TREE_SIZE][CHARSET];
bool vleaf[TREE_SIZE];  // 记录字符串的结尾的结点
bool hleaf[TREE_SIZE];

bool check(char y, char x) // 检查第 y 行第 x 列的填充是否合理
{
	int pos = 0;
	++y;
	sfor(i, y)
		if ((pos = V(pos, mat[i][x] - 97)) == 0)
			return false;
	if (y == nro && !vleaf[pos])
		return false;
	return true;
}

void dfs(char y, char x, int nod) // 填充第 y 行第 x 列。前一个字符对应的结点为 nod
{
	sfor(i, 26)
	{
		if (!H(nod, i))
			continue;
		mat[y][x] = i + 97;
		if ((x == nco - 1 && !hleaf[H(nod, i)])
			|| !check(y, x))
			continue;
		if (x == nco - 1)
		{
			if (y == nro - 1)
				++res;
			else
				dfs(y + 1, 0, 0);
		}
		else
			dfs(y, x + 1, H(nod, i));
	}
	mat[y][x] = 0;
}

int main()
{
	int cur = 0, ch = 0, pos;
	scanf("%d%d%d%d",
		&nro, &nvert, &nco, &nhorz);
	sfor(i, nvert)
	{
		pos = 0;
		while (ch < 97)
			gch();
		while (ch > 96)
		{
			ch -= 97;
			if (V(pos, ch) == 0)
				V(pos, ch) = ++cur;
			pos = V(pos, ch);
			gch();
		}
		vleaf[cur] = true;
	}
	sfor(i, nhorz)
	{
		pos = 0;
		while (ch < 97)
			gch();
		while (ch > 96)
		{
			ch -= 97;
			if (H(pos, ch) == 0)
				H(pos, ch) = ++cur;
			pos = H(pos, ch);
			gch();
		}
		hleaf[cur] = true;
	}
	dfs(0, 0, 0);
	printf("%lld\n", res);
	return 0;
}