三种最短路模板

一、Floyd算法——只有五行代码的算法

算法思想：

从节点i到节点j的最短路径只有2种可能：

1)直接从节点i到节点j

2)从节点i经过若干个节点k到节点j

假设dis(i,j)为节点i到节点j的最短路径的距离

对于每一个节点k，我们检查dis(i,k)+dis(k,j) < dis(i,j)是否成立，

如果成立，证明从i到k再到j的路径比i直接到j的路径短.

于是dis(i,j) = dis(i,k) + dis(k,j)，这样一来，当我们遍历完所有k，dis(i,j)中记录的便是节点i到节点j的最短路径的距离

缺点：时间复杂度太高 O(n^3)

模板：

void Floyd()
{
	for(int k = 1; k <= N; k++)  
        for(int i = 1; i <= N; i++) 
            for(int j = 1; j < N; j++) 
                if(dis[i][k] + dis[k][j] < dis[i][j]) 
                    dis[i][j] = dis[i][k] + dis[k][j];
}
        

二、Dijkstra算法

如下图：

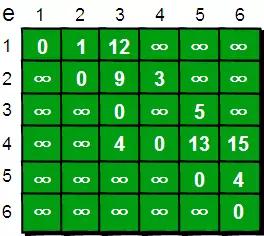
我们还需要用一个一维数组 dis 来存储 1 号顶点到其余各个顶点的初始路程，如下：

 

既然是求 1 号顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。

通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后，即 1 号顶点到 2 号顶点的最短路程就是dis[2]的值

既然选了 2 号顶点，接下来看 2 号顶点有 2-3 和 2-4 这两条边。

先思考通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在来比较 dis[3]和 dis[2]+e[2][3]的大小。其中 dis[3]表示 1 号顶点到 3 号顶点的路程，dis[2]+e[2][3]中 dis[2]表示 1 号顶点到 2 号顶点的路程，e[2][3]表示 2-3 这条边。所以 dis[2]+e[2][3]就表示从 1 号顶点先到 2 号顶点，再通过 2->3 这条边，到达 3 号顶点的路程。

我们发现 dis[3]=12，dis[2]+e[2][3]=1+9=10，dis[3]>dis[2]+e[2][3]，因此 dis[3]要更新为 10，以此类推。

基本思想：每次找到离源点最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。

时间复杂度：O(n^2)

代码：

1.初始化

void mem()
{
	for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        if(i==j)e[i][j]=0;
        else e[i][j]=INF;
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&v1,&v2,&w);
        e[v1][v2]=w;
    }
    for(int i=1;i<=n;i++)dis[i]=e[1][i];
    for(int i=1;i<=n;i++)vis[i]=0;
    vis[1]=1; 
}

2.算法核心

void Dijkstra()
{
    for(int i=1;i<=n-1;i++)
    { 
        int min_num=INF;
        int min_index=0;
        for(int k=1;k<=n;k++) 
            if(min_num>dis[k] && book[k]==0)
            {
                min_num=dis[k];
                min_index=k;
            }
        book[min_index]=1; 
        for(int j=1;j<=n;j++)
            if(e[min_index][j]dis[min_index]+e[min_index][j])
                    dis[j]=dis[min_index]+e[min_index][j];
    }
}

三、SPFA算法

算法优点：

 1.时间复杂度比普通的Dijkstra和Ford低。

 2.能够计算负权图问题。 

实现方法：

1.存入图。可以使用链式前向星或vector。

2.开一个队列，先将开始的节点入队。

3.每次从队列中取出一个节点X，遍历与X相通的Y节点，比对  b的长度 和 a的长度+ a与b的长度

 如果a的长度+ a与b的长度 > b的长度——需要更新。

1）存入最短路。

2）由于改变了原有的长度，所以需要往后更新，与这个节点相连的最短路。(即：判断下是否在队列，在就不用重复，不在就加入队列，等待更新)。

3）在这期间可以记录这个节点的进队次数，判断是否存在负环。

 4.直到队空。

判断有无负环：如果某个点进入队列的次数超过N次则存在负环

代码：

void SPFA()//核心代码
{
	queue  q;
	memset(vis,inf,sizeof(vis));
	memset(ven,0,sizeof(ven));
	memset(nums,0,sizeof(nums));
	vis[s]=0;
	ven[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop(); 
		ven[x]=0; 
		for(int i=pre[x]; ~i; i=a[i].next)
		{
			int y=a[i].y;
			if(vis[y]>vis[x]+a[i].time)
			{
				vis[y]=vis[x]+a[i].time;
				if(!ven[y])
				{
					q.push(y);
					ven[y]=1; 
				}
			}
		}
	}
}

存图代码：（链式前向星）

void add(int x,int y,int k)//链式前向星，加入节点
{
	a[cent].y=y;
    a[cent].time=k;
    a[cent].next=pre[x];
	pre[x]=cent++;
}