八大排序:Java实现八大排序及算法复杂度分析
目录
QUESTION:八大排序:Java实现八大排序及算法复杂度分析
ANSWER:
一:冒泡排序
1.算法分析
2.时间复杂度分析
3.代码
二:选择排序
1.算法分析
2.时间复杂度分析
3.代码
三:插入排序
1.算法分析
2.时间复杂度分析
3.代码
四:归并排序
1.算法分析
2.时间复杂度分析
3.代码
五:堆排序
1.算法分析
2.时间复杂度分析
3.代码
六:快速排序
1.算法分析
2.时间复杂度分析
3.代码
QUESTION:八大排序:Java实现八大排序及算法复杂度分析
ANSWER:
一:冒泡排序
1.算法分析
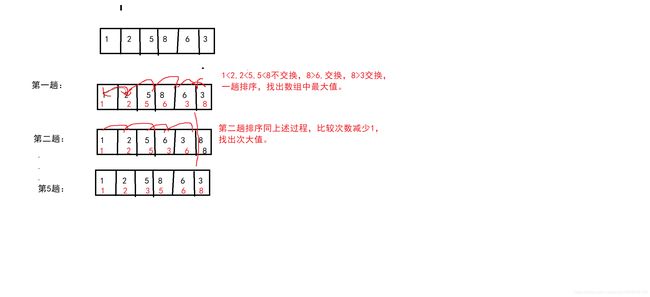
冒泡排序是对于一个数组,从第一个数开始,与下一个数进行比较,大的冒后面,小的冒前面,相邻元素依次比较,完成一次循环,继续下一次循环,直至数组有序。
图示:
2.时间复杂度分析
由于冒泡排序是两层for循环,所以T=O(n^2)。
3.代码
**
* 冒泡排序
*/
public class BubbleSort {
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
/**
* 比较相邻元素大小,每次缩减一
* @param arr
*/
public static void bubbleSort(int []arr){
if (arr==null){
return;
}
for (int i = arr.length-1; i >0 ; i--) {
for (int j = 0; j arr[j+1]){
swap(arr,j,j+1);
}
}
}
}
}
二:选择排序
1.算法分析
选择排序是选择数组第一个元素假设为最小元素,与后面的所以元素比较,比其它元素大就交换位置,完成一次循环就从第二个元素开始依次上述过程比较,直至数组有序。
图示:
2.时间复杂度分析n^
由于选择排序两层for循环,所以T=O(n^2)。
3.代码
/**
* 选择排序
*/
public class SelectionSort {
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
/**
* 假设第一个值为最小元素,每次循环与后一个元素比较找到最小元素
* @param arr
*/
public static void selectionSort(int []arr){
if (arr==null){
return;
}
for (int i = 0; i
三:插入排序
1.算法分析
插入排序是从数组第二个元素开始,找前面的数,比较大小,如果前面的数大,就交换位置,然后继续向前比较,。每次从第几个元素开始遍历时都把较小的元素插入到该元素前面,使其前面数组有序,完成一次循环,继续循环下一个元素直至数组有序。
图示:
2.时间复杂度分析
由于插入排序两层for循环,T=O(n^2)。
3.代码
public class InsertionSort {
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void insertionSort(int []arr){
if (arr==null){
return;
}
for (int i = 1; i =0&&arr[j]>arr[j+1]; j--) {
swap(arr,j,j+1);
}
}
}
}
四:归并排序
1.算法分析
归并排序是利用二分的思想,不断的将数组进行分割为两部分,依次比较每部分的最小元素,将最小的元素放入辅助数组,直到所有元素都插入数组,完成排序。
图示:
2.时间复杂度分析
由于归并排序是合并的思想,所有T=O(n*logn)。
3.代码
public class MergeSort {
/**
* 将数组分段排序插入,然后归并排序
* @param arr
* @param l
* @param m
* @param r
*/
public static void merge(int []arr,int l,int m,int r){
int []help=new int[r-l+1];
int i=0;
int p1=l;
int p2=m+1;
while (p1<=m&&p2<=r){
help[i++]=arr[p1]<=arr[p2]?arr[p1++]:arr[p2++];
}
while (p1<=m){
help[i++]=arr[p1++];
}
while (p2<=r){
help[i++]=arr[p2++];
}
for (int j = 0; j =r){
return;
}
int mid=((r-l)>>1)+l;
mergeSort(arr,l,mid);
mergeSort(arr,mid+1,r);
merge(arr,l,mid,r);
}
/**
* 数组归并排序
*/
public static void mergeSort(int []arr){
if (arr==null){
return;
}
mergeSort(arr,0,arr.length-1);
}
}
五:堆排序
1.算法分析
堆排序的思想是根据二叉树的大根堆和小根堆的概念形成,首先依照数组建立大根堆,之后为了防止某一个元素的变化而引起整个大根堆的变化,建立一个修改二叉树为大根堆的方法,该数组保持大根堆的排序。之后交换大根堆元素,得到有序数组。
图示:
2.时间复杂度分析
堆排序建立大根堆的过程,T=O(n*logn)。
3.代码
/**
* 堆排序,大根堆,小根堆
*/
public class HeapSort{
/**
* 建立大根堆,当孩子结点大于根结点进行交换,没有进行左右孩子结点的比较
* @param arr
* @param index
*/
public static void heapInsert(int []arr,int index){
while(arr[index]>arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index=(index-1)/2;
}
}
/**
* 修改数组为大根堆
* @param arr
* @param index
* @param size
*/
public static void heapModifiy(int []arr,int index,int size){
int left=2*index+1;
while(leftarr[left]&&(left+1)arr[largest]?index:largest;
if (largest==index) {
break;
}
swap(arr,index,largest);
index=largest;
left=2*index+1;
}
}
/**
* 堆排序
* @param arr
*/
public static void heapSort(int []arr){
if (arr==null||arr.length==0) {
return;
}
for (int i=0;i0){
heapModifiy(arr,0,size);
swap(arr,0,--size);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
六:快速排序
1.算法分析
快速排序的基本思想是有荷兰国旗问题的相似,先是随机产生一个范围进行数组的划分,小于区域在左边,等于区域在中间,等于区域在右边,直至数组完成排序。
图示:
2.时间复杂度分析
快速排序T=O(n*logn)。
3.代码
/**
* 快速排序
*/
public class QuickSort {
/**
*给定范围划分大于区域,等于区域,小于区域排序
* @param arr
* @param l
* @param r
* @return
*/
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr,++less,l++);
}
else if (arr[l]==arr[r]){
l++;
}
else{
swap(arr,--more,l);
}
}
swap(arr,more,r);
return new int[]{less+1,more};
}
/**
* 产生一个随机范围进行划分排序
* @param arr
* @param l
* @param r
*/
public static void quickSort(int []arr,int l,int r){
if (l