c++:求解二元二次方程组(解析解)
这个问题从产生到解决,困扰了LZ快一周(当然因为中间也有其他事情要做),本来从LZ的角度是想找第三方库使用,不要说matlab就可以啊o(╥﹏╥)o,确实matlab一个solve函数就解决问题了,但是问题是不能用matlab,所以第一方案排除。
用第三方库?google了半天,发现一个gsl库确实可以求解二元二次方程组,但是也有问题,1)只能求解出一个解,而且无法求解复数解(源代码定义中没有复数定义,除非自己扒源程序,自己写);2)使用的是优化算法,例如牛顿迭代等,所求出的是近似解,非解析解,也就是说求得的结果并不精确。而且初始值的设定会影响迭代结果,容易进入局部最优。3)复数解无法收敛。
PS:花钱的库还是算了,毕竟也不是特别难解决的问题。。。
只剩一个方案:自己动手,丰衣足食O(∩_∩)O哈哈~
列出基本的问题:
a1x2+b1xy+c1y2+d1x+e1y+f1=0
a2x2+b2xy+c2y2+d2x+e2y+f2=0
求上述方程的解(包含复数),也就是两个二次曲线的交点。
step 1: 利用两式相减,用x来表示y
得到类似如下的方程:
(Bx+D)y=−Ax2−Cx−E
其中的A,B,C,D,E都是用 a1−f1,a2−f2 所表示的。
step 2:带入原方程得到关于 x 的一元四次方程
M4x4+M3x3+M2x2+M1x+M0=0
将四次项归一化
x4+bx3+cx2+dx+e=0
step 3: 利用费拉里法求一元四次方程
具体对费拉里法求解一元四次方程的推导:https://baike.baidu.com/item/%E4%B8%80%E5%85%83%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B
这里就不在解释了,因为公式很多,手打太浪费时间了。
讲了这么多,贴出源代码:(如果有小伙伴有更好的方法可以和LZ私聊哦)
#include 6, 1> & _par1,
Eigen::Matrix6, 1> & _par2,
Eigen::Matrix5, 1> & _y2x_par,
Eigen::Matrix, 5, 1> &_quartic_par)
{
double A, B, C, D, E;
double a1, b1, c1, d1, e1, f1, a2, b2, c2, d2, e2, f2;
a1 = _par1[0];
b1 = _par1[1];
c1 = _par1[2];
d1 = _par1[3];
e1 = _par1[4];
f1 = _par1[5];
// std::cout << a1 << " " << b1 << " " << c1 << " " << d1 << " " << e1 << " " << f1 << std::endl;
a2 = _par2[0];
b2 = _par2[1];
c2 = _par2[2];
d2 = _par2[3];
e2 = _par2[4];
f2 = _par2[5];
// std::cout << a2 << " " << b2 << " " << c2 << " " << d2 << " " << e2 << " " << f2 << std::endl;
A = a1*c2 - c1*a2;
B = b1*c2 - c1*b2;
C = d1*c2 - c1*d2;
D = e1*c2 - c1*e2;
E = f1*c2 - c1*f2;
_y2x_par << A, B, C, D, E;
// std::cout << "A-E: \n";
// std::cout << A << " " << B << " " << C <<" " << D << " " << E << std::endl;
double M0, M1, M2, M3, M4;
M4 = a1*B*B - b1*A*B + c1*A*A;
M3 = 2*a1*B*D - b1*A*D - b1*B*C + 2*c1*A*C + d1*B*B - e1*A*B;
M2 = a1*D*D - b1*C*D - b1*B*E + c1*C*C + 2*c1*A*E + 2*d1*B*D - e1*A*D - e1*B*C + f1*B*B;
M1 = -b1*D*E + 2*c1*C*E + d1*D*D - e1*C*D - e1*B*E + 2*f1*B*D;
M0 = c1*E*E - e1*D*E + f1*D*D;
// std::cout << "m4-m0: \n";
// std::cout << M4 << " " << M3 << " " << M2 << " " << M1 << " " << M0 << std::endl;
//
double b, c, d, e;
b = M3 / M4;
c = M2 / M4;
d = M1 / M4;
e = M0 / M4;
// std::cout << "b, c, d, e: \n";
// std::cout << " " << b << " " << c << " " << d<< " " << e << " \n";
_quartic_par << 1.0, b, c, d, e;
}
//extract a root
void sqrtn(const std::complex &_input, double n,
std::complex & _out)
{
// double r = sqrt(_input.real()*_input.real() + _input.imag()*_input.imag());
// std::cout << _input << std::endl;
double r = hypot(_input.real(), _input.imag());
// std::cout << "the norm is " << r << std::endl;
if(r > 0.0)
{
double a = atan2(_input.imag(), _input.real());
// std::cout << "the a is: " << a << std::endl;
// double a = arg(_input);
n = 1 / n;
r = pow(r, n);
a *= n;
_out.real() = r * cos(a) ;
_out.imag() = r * sin(a);
}
else
{
_out.real() = 0.0;
_out.imag() = 0.0;
}
// std::cout << "out :" << _out << std::endl;
}
void Ferrari(Eigen::Matrix, 5, 1> & _quartic_par,
Eigen::Matrix, 4, 1> & _x)
{
std::complex a = _quartic_par[0];
std::complex b = _quartic_par[1];
std::complex c = _quartic_par[2];
std::complex d = _quartic_par[3];
std::complex e = _quartic_par[4];
std::complex P = (c*c + 12.0*e - 3.0*b*d) / 9.0;
std::complex Q = (27.0*d*d + 2.0*c*c*c + 27.0*b*b*e - 72.0*c*e - 9.0*b*c*d) / 54.0;
// std::cout << "P: " << P << " \nQ: " << Q << std::endl;
std::complex D, u, v;
// D = cabs(sqrt(Q*Q - P*P*P));
sqrtn(Q*Q - P*P*P, 2.0, D);
// std::cout << "D: " << D << std::endl;
u = Q + D;
v = Q - D;
// std::cout << "u: " << u << " \nv: " << v << std::endl;
if(v.real()*v.real() + v.imag()*v.imag() > u.real()*u.real() + u.imag()*u.imag())
{
sqrtn(v, 3.0, u);
}
else
{
sqrtn(u, 3.0, u);
}
// std::cout <<"u: " << u << std::endl;
std::complex y;
if(u.real()*u.real() + u.imag()*u.imag() > 0.0)
{
v = P / u;
std::complex o1(-0.5,+0.86602540378443864676372317075294);
std::complex o2(-0.5,-0.86602540378443864676372317075294);
std::complex &yMax = _x[0];
double m2 = 0.0;
double m2Max = 0.0;
int iMax = -1;
for(int i = 0; i < 3; ++i)
{
y = u + v + c / 3.0;
u *= o1;
v *= o2;
a = b*b + 4.0*(y-c);
m2 = a.real()*a.real() + a.imag()*a.imag();
if(0==i || m2Max < m2)
{
m2Max = m2;
yMax = y;
iMax = i;
}
}
y = yMax;
}
else
{//cubic equation
y = c / 3.0;
}
std::complex m;
sqrtn(b*b + 4.0*(y-c), 2.0, m);
if(m.real()*m.real() + m.imag()*m.imag() >= DBL_MIN)
{
std::complex n = (b*y - 2.0*d) / m;
sqrtn((b+m)*(b+m) - 8.0*(y+n), 2.0, a);
_x[0] = (-(b+m) + a) / 4.0;
// std::cout << "_x[0]: " << _x[0] << std::endl;
_x[2] = (-(b+m) - a) / 4.0;
// std::cout << "_x[1]: " << _x[1] << std::endl;
sqrtn((b-m)*(b-m) - 8.0*(y-n), 2.0, a);
_x[1] = (-(b-m) + a) / 4.0;
_x[3] = (-(b-m) -a) / 4.0;
// std::cout << "_x[2]: " << _x[2] << std::endl;
// std::cout << "_x[3]: " << _x[3] << std::endl;
}
else
{
sqrtn(b*b - 8.0*y, 2.0, a);
_x[0] = _x[1] = (-b + a) / 4.0;
_x[2] = _x[3] = (-b - a) / 4.0;
}
// for(int i = 0; i <4; i++)
// {
// std::cout << _x[i] << std::endl;
// }
}
void compute_y(Eigen::Matrix, 4, 1> &_x,
Eigen::Matrix5, 1> &_y2x_par,
Eigen::Matrix, 4, 1> &_y)
{
for(int i = 0; i < 4; i++)
{
_y[i] = (-_y2x_par[0]*_x[i]*_x[i] - _y2x_par[2]*_x[i] - _y2x_par[4]) / (_y2x_par[1]*_x[i] + _y2x_par[3]);
// std::cout << "_y[" << i << "]" << _y[i] << std::endl;
}
}
int main(int argc, char **argv) {
Eigen::Matrix6, 1> ic1, ic2;
ic1 <<414181, -12635.8, 398758, -9.53484e+08, -4.16931e+08, 5.00382e+11;
ic2 << 923938, -41764.7, 932015, -2.10858e+09, -9.79279e+08, 6.2537e+11;
Eigen::Matrix, 5, 1> quartic_par;
Eigen::Matrix5, 1> y2x_par;
// quadratic2quartic(ic1, ic2, quartic_par);
quadratic2quartic(ic1, ic2, y2x_par, quartic_par);
Eigen::Matrix, 4, 1> x, y;
Ferrari(quartic_par, x);
compute_y(x, y2x_par, y);
std::cout <<"the result :" << std::endl;
for(int i = 0; i < 4; i++)
{
std::cout << "x: " << x[i] << "\ty: " << y[i] << std::endl;
}
// std::cout << "Hello, world!" << std::endl;
return 0;
} 使用了Eigen处理矩阵会比较方便。
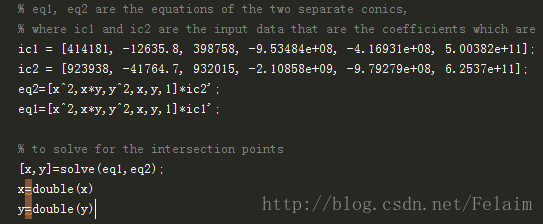
使用matlab对上述算法进行验证:
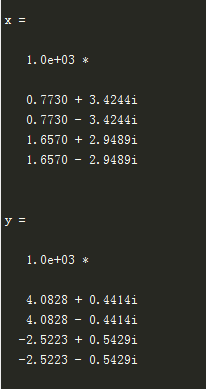
最后运行结果如下所示:
好,最后检验完毕。最后感慨一下还是matlab功能强大,如果要使用c++还是要对具体算法原理了解,才能编写代码,对编程能力、算法理解要求更高,所以小伙伴们自行决定需要什么工具哦O(∩_∩)O哈哈~解决一个问题好开心(。◕ˇ∀ˇ◕)