力扣（LeetCode）Java刷题 简单+中等（第二期）

2020年2月23日

1. 字符串转换整数 （中等题）
   题目描述：
   首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。
   当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。 该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。
   注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。在任何情况下，若函数不能进行有效的转换时，请返回 0。
   说明：
   假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (2147483647) 或 INT_MIN (−2147483648) 。
   示例 1:
   输入: “42”
   输出: 42
   示例 2:
   输入: " -42"
   输出: -42
   解释: 第一个非空白字符为 ‘-’, 它是一个负号。我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。
   示例 3:
   输入: “4193 with words”
   输出: 4193
   解释: 转换截止于数字 ‘3’ ，因为它的下一个字符不为数字。
   示例 4:
   输入: “words and 987”
   输出: 0
   解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。因此无法执行有效的转换。
   示例 5:
   输入: “-91283472332”
   输出: -2147483648
   解释: 数字 “-91283472332” 超过 32 位有符号整数范围。 因此返回-2147483648
   方法代码：

class Solution {
    public int myAtoi(String str) {
       if(str == "" || str == null || str.length() == 0) return 0;
			int n = 0;
			boolean temp1 = false;
			boolean temp2 = false;
	        int start = 0;
	        //找到第一个非零字符
	        for (int i = 0; i < str.length(); i++){
	            if(str.charAt(i) == 32)
	                continue;
	            else{
	                 start = i;
	                 break;
	            }
	        }
	        //判断符号
	        if(str.charAt(start) == 45 ){
                temp1 = true;
                start++; 
            }
				
            else if(str.charAt(start) == 43 ){
                temp1 = false;
                start++;
            }
            逐个将字符转成数字
			for (int i = start; i < str.length(); i++) {
	                
				 if((str.charAt(i) > 47 && str.charAt(i) < 58)) {
				  //判断字符是否大于int类型的范围
					if(temp1 && (n*-1 <Integer.MIN_VALUE/10 || (str.charAt(i) > 56 && n*-1 ==Integer.MIN_VALUE/10)))
						return -2147483648;
						else if(!temp1 &&( n >Integer.MAX_VALUE/10 || (str.charAt(i) > 55 && n ==Integer.MAX_VALUE/10)))
						return 2147483647;
						else
						n = n*10 + str.charAt(i) - 48;
				}
				
				else {
					temp2 = true;
					break;
				}
			}
			if(temp2 && n == 0)
				return 0;
			else if(temp1)
				return n *= -1;
			else
				return n;
            
    }
}

方法解析：
首先要找到第一个非空字符，之后判断正负符号，然后就开始将字符串格式转化为数字，在这期间需注意字符串转换成的数字有没有超过int类型的范围，如果超过就返回int的最大或最小值，还要注意中间有没有不是数字字符的字符，如果有就终止转换。

2.回文数（简单题）
判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。
示例 1:
输入: 121
输出: true
示例 2:
输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。
方法代码：

class Solution {
    public boolean isPalindrome(int x) {
        if(x < 0 || ( x % 10 == 0 && x != 0))   return false;
		 	int n = 0;
		 	int temp = x;
		 	while(temp > n){
                 n = n*10 + temp% 10;
                 temp = temp / 10;

             }
        return n== temp || n/10 == temp;
    }
}

方法解析：
将数字本身反转，然后将反转后的数字与原始数字进行比较，如果它们是相同的，那么这个数字就是回文。但是，如果反转后的数字大于 int.MAX，我们将遇到整数溢出问题。按照第这个想法，为了避免数字反转可能导致的溢出问题，只考虑反转数字的一半，毕竟，如果该数字是回文，其后半部分反转后应该与原始数字的前半部分相同。例如，输入 1221，我们可以将数字 “1221” 的后半部分从 “21” 反转为 “12”，并将其与前半部分 “12” 进行比较，因为二者相同，我们得知数字 1221 是回文。

3.盛最多水的容器（中等题）
给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂 直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。

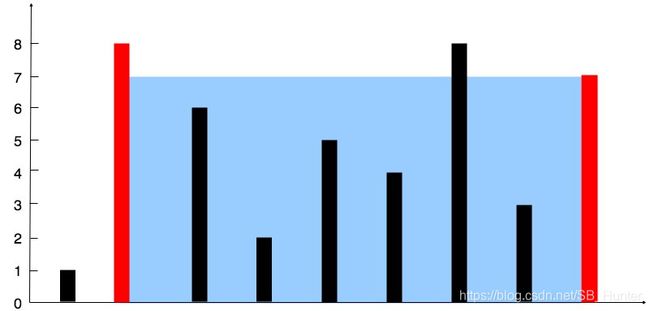
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
方法代码：

class Solution {
    public int maxArea(int[] height) {
        int max = 0;
		int i = 0, j = height.length - 1 ;
        int area = 0;
        while(i < j){
            area = height[i] < height[j] ?
                    Math.max(area, (j-i)*height[i++]):
                    Math.max(area, (j-i)*height[j--]);
        }
        return area;
    }
}

方法解析：
算法流程： 设置双指针 i,j分别位于容器壁两端，根据规则移动指针（后续说明），并且更新面积最大值area，直到 i == j 时返回 area。
指针移动规则与证明： 每次选定围成水槽两板高度 h[i],h[j]中的短板，向中间收窄1格。以下证明：
设每一状态下水槽面积为 S(i, j),(0 <= i < j < n)，由于水槽的实际高度由两板中的短板决定，则可得面积公式 S(i, j) = min(h[i], h[j]) × (j - i)。
在每一个状态下，无论长板或短板收窄11格,都会导致水槽底边宽度 −1：
若向内移动短板，水槽的短板 min(h[i],h[j]) 可能变大，因此水槽面积 S(i, j)可能增大。
若向内移动长板，水槽的短板 min(h[i],h[j]) 不变或变小，下个水槽的面积一定小于当前水槽面积。
因此，向内收窄短板可以获取面积最大值。换个角度理解：
若不指定移动规则，所有移动出现的 S(i, j)S(i,j) 的状态数为 C(n, 2)，即暴力枚举出所有状态。
在状态 S(i, j)下向内移动短板至S(i+1,j)（假设 h[i] < h[j]h[i] 短板高度：相比 S(i, j)相同或更短（<= h[i]）；
底边宽度：相比 S(i, j)更短。
因此所有消去的状态的面积都 < S(i, j)

4. 整数转罗马数字(中等题）
   罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。
   字符 数值
   I 1
   V 5
   X 10
   L 50
   C 100
   D 500
   M 1000
   例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
   通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
   I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
   X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
   C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
   给定一个整数，将其转为罗马数字。输入确保在 1 到 3999 的范围内。
   示例 1:
   输入: 3
   输出: “III”
   示例 2:
   输入: 1994
   输出: “MCMXCIV”
   解释: M = 1000, CM = 900, XC = 90, IV = 4.
   方法代码：

class Solution {
    public String intToRoman(int num) {
         if(num<1 || num > 3999) return "";
		 StringBuilder str = new StringBuilder();
		 int[] num1 = {1000,900,500,400,100,90,50,40,10,9,5,4,1};
		 String[] l = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
		 int index = 0;
		 while(index < num1.length){
              while(num >= num1[index]) {
				 str.append(l[index]);
				 num -= num1[index];
		
		    }
            index++;
         }
			
		 return str.toString();
    }
}

方法解析：
在表示一个较大整数的时候，“罗马数字”的设计者不会让你都用 11 加起来，我们总是希望写出来的“罗马数字”的个数越少越好，以方便表示，并且这种表示方式还应该是唯一的。所以我们要从最大的位数开始转换。
这道问题，类似于用最少的纸币凑成一个整数，贪心算法的规则如下：
每一步都使用当前较大的罗马数字作为加法因子，最后得到罗马数字表示就是长度最少的。

5. 罗马数字转整数（简单题）
   罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。
   字符 数值
   I 1
   V 5
   X 10
   L 50
   C 100
   D 500
   M 1000
   例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
   I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
   X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
   C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
   给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。
   示例 1:
   输入: “III”
   输出: 3
   示例 2:
   输入: “MCMXCIV”
   输出: 1994
   解释: M = 1000, CM = 900, XC = 90, IV = 4.
   方法代码：

class Solution {
    public int romanToInt(String s) {
         Map<Character, Integer> map = new HashMap<>();   
		 map.put('I', 1);
		 map.put('V', 5);
		 map.put('X', 10);
		 map.put('L', 50);
		 map.put('C', 100);
		 map.put('D', 500);
		 map.put('M', 1000);
		 int n = 0;
		char[] c = s.toCharArray();
		for(int i = 0 ; i < c.length ; i++) {
			int j = i+1;
			if(j < c.length && map.get(c[i]) < map.get(c[j])) {
				n = map.get(c[j]) + n - map.get(c[i]);
				i++;
			}
			else
				n += map.get(c[i]);
		}
		return n;
		 
    }
}

方法解析：首先将所有罗马数字所代表的阿拉伯数字一次存储在Map数组中，该方法最重要的是如果字符串中该字符所代表的值大于该字符后面的字符所代表的值，那么就应该减去该字符的值，所以判断每个字符的与后一个字符的关系，逐个加该符号的值或减去该符号的值。

6.最长公共前缀(简单题）
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀，返回空字符串 “”。
示例 1:
输入: [“flower”,“flow”,“flight”]
输出: “fl”
示例 2:
输入: [“dog”,“racecar”,“car”]
输出: “”
解释: 输入不存在公共前缀。
方法代码：

class Solution {
    public String longestCommonPrefix(String[] strs) {
         if(strs.length == 1) return strs[0];
		 if(strs.length == 0) return "";
		 String str = "";
		 char[] temp = strs[0].toCharArray();
		 for(int j = 0; j < temp.length ; j++) {
			 for(int i = 1 ; i < strs.length; i++) {
                 if(j >= strs[i].length() )
                 return str;
				 if(temp[j] != strs[i].charAt(j))
					 return str;
			 }
			 str += temp[j];
		 }
		return str;
    }
}

方法解析：该方法先将第一个字符串的每个字符逐个与剩下的字符串的相应位置的字符进行比较，如遇到不相等的立马返回已得前缀字符串。