03-树3 Tree Traversals Again (25 分)（前中序变后序）

03-树3 Tree Traversals Again (25 分)
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

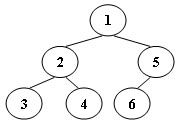
Figure 1
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: “Push X” where X is the index of the node being pushed onto the stack; or “Pop” meaning to pop one node from the stack.

Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1

谷歌翻译：
03-树3树遍历（25分）
可以使用堆栈以非递归方式实现顺序二进制树遍历。例如，假设当遍历6节点二叉树（编号为1到6的键）时，堆栈操作为： push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop().然后可以从该操作序列生成唯一的二叉树（如图1所示）。你的任务是给出这棵树的后序遍历序列。

输入规格：
每个输入文件包含一个测试用例。对于每种情况，第一行包含正整数N（≤30），其是树中节点的总数（因此节点从1到N编号）。然后是2N行，每行描述一种格式的堆栈操作：“Push X”，其中X是被推入堆栈的节点的索引;或“Pop”表示从堆栈中弹出一个节点。

输出规格：
对于每个测试用例，在一行中打印相应树的后序遍历序列。保证存在解决方案。所有数字必须用一个空格分隔，并且在行的末尾不能有额外的空格。

样本输入：
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

样本输出：
3 4 2 6 5 1

看一下下面的简图便于理解：

题解：
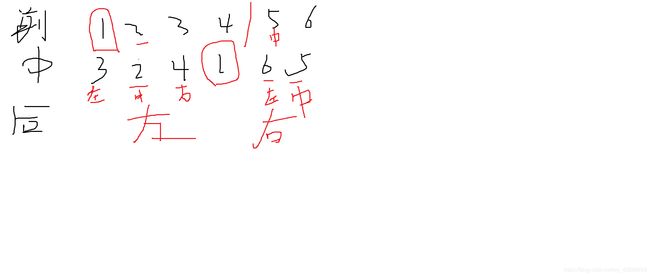
前序：1 2 3 4 5 6
中序：3 2 4 1 6 5
通过 输入的 push 顺序，得到前序遍历的数组
通过 push 和 pop 顺序，得到 中序遍历的数组
通过前序和中序的数组，可以唯一确定一个后序遍历数组。

后序序列就是在每个子序列的末尾存储当前找出来的根节点，，然后进行递归直到结束

因为后序序列就是根节点在最后存储的。每次只存储当前的根节点，将根节点存储完毕，也就是结束了。

关键地方：就是在中序中找出根节点位置，以及左子序列的长度，右子序列的长度；以及当前后序序列中当前子序列的其实位置下标；还有前序序列中根节点的下标；

前序序列根节点的下标变化：1、PreL+1 2、PreL+L+1
中序序列中子序列的起始位置：1、InL 2、InL+L+1
后序序列中要存储的根节点的起始位置，也就是当前子序列的第一个位置：1、LastL 2、LastL+L
左右序列的长度：L和R

具体注释请看代码中的注释：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
#define maxn 1000005
#define mod 7654321

stack<int> s;
int pre[1000],mid[1000],last[1000];

//1 2 3 4 5 6
//3 2 4 1 6 5
//通过 输入的 push 顺序，得到前序遍历的数组
//通过 push 和 pop 得到 中序遍历的数组
//通过前序和中序的数组，可以唯一确定一个后序遍历数组。

//参数：PreL为当前前序序列的起始位置，即根节点位置
//InL为当前中序序列中的左或右子树的起始位置
//LastL为后序序列中子序列起始位置的下标
//n为当前左或右子树的长度

void Solve(int PreL,int InL,int LastL,int n)
{
    if(n==0)//若没有节点直接返回
        return;
    if(n==1)//若只有一个节点，直接将其赋值给后序第一个元素
    {
        last[LastL]=pre[PreL];
        return;
    }
    int Root=pre[PreL];//存储当前子序列的根节点的值
    //LastL+n-1 就是当前序列的最后一个位置，因为根节点一定在LastL为当前子序列起始位置，
	//n为当前序列总长度，-1为当前序列最后一个位置的下标
    last[LastL+n-1]=Root;//起始位置加总长-1就是最后一个位置
    int i;

    //在当前子序列长度n中找到根节点位置
    for(i=0;i<n;i++)
    {
        if(mid[InL+i]==Root)//找到的i的位置为当前子序列中的位置
            break;
    }
    int L=i,R=n-i-1;//当前左右子序列的长度

    //递归解决左右

    /*后一个前序序列的根节点(第一个参数PreL):
	1、当前节点的下一个节点（当前左子树的根）即PreL+1
	2、以及当前节点往后推左子树的长度L(当前右子树的根)即PreL+1+L
	//中序序列开始查找的位置（第二个参数InL）
	1、当前左子树的起点往后走即InL
	2、当前右子树的起点往后走左子树的长度L即InL+1+L
	//后序序列的存储位置,当前左子树的起点位置（第三个参数postL）
	1、即当前位置postL
	2、往后走L到右子树起点即postL+L
	//第四个参数（L,R）
	存储当前左右子树的长度，最后将其值都赋值给n
	*/
    Solve(PreL+1,InL,LastL,L);
    Solve(PreL+L+1,InL+L+1,LastL+L,R);
}

int main()
{
    int n,a,j=0,k=0;

    string str;
    cin>>n;
    for(int i=0;i<2*n;i++)
    {
        cin>>str;
        if(str=="Push")
            cin>>a,s.push(a),pre[j++]=a;
        if(str=="Pop")
            mid[k++]=s.top(),s.pop();
    }

    Solve(0,0,0,n);

    for(int i=0;i<n;i++)
    {
        if(i==0)
            cout<<last[i];
        else
            cout<<" "<<last[i];
    }
    cout<<endl;
    return 0;
}