第七章 - 排序
1.已知关键字序列 5 , 8 , 12 , 19 , 28 , 20 , 15 , 22 是小根堆(最小堆),插入关键字 3 ,调整后得到的小根堆是 。
-
3,5,12,8,28,20,15,22,19 -
3,5,12,19,20,15,22,8,28 -
3,8,12,5,20,15,22,28,19 -
3,12,5,8,28,20,15,22,19
解析: 小顶堆特点-根节点和不是叶子节点的节点。小于它的左孩子,也小于它的右孩子
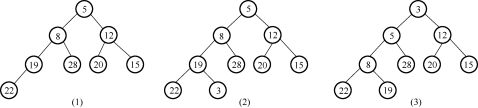
根据关键字序列得到的小顶堆的二叉树形式如下图所示。
插入关键字3时,先将其放在小顶堆的末端,如图(2)所示。再将该关键字向上进行调整,得到的结果如图(3)所示。所以,调整后的小顶堆序列为3,5,12,8,28,20,15,22,19。
2.若数据元素序列11,12,13,7,8,9,23,4,5是采用下列排序方法之一得到的第二趟排序后的结果,则该排序算法只能是()。
-
冒泡排序 -
插入排序 -
选择排序 -
二路归并排序
解析:
解答本题需要对各种排序算法的特点极为清楚。对于冒泡排序和选择排序,每一趟都能确定一个元素的最终位置,而题目中,前2个元素和后2个元素均不是最小或最大的2个元素并按序排列。选项D中的2路归并排序,第一趟排序结束都可以得到若干个有序子序列,而此时的序列中并没有两两元素有序排列。插入排序在每趟排序后能确定前面的若干元素是有序的,而此时第二趟排序后,序列的前三个元素是有序的,符合其特征。
3.采用递归方式对顺序表进行快速排序,下列关于递归次数的叙述中,正确的是(D)
-
递归次数与初始数据的排列次序无关 -
每次划分后,先处理较长的分区可以减少递归次数 -
每次划分后,先处理较短的分区可以减少递归次数 -
递归次数与每次划分后得到的分区处理顺序无关
解析:答案选D
递归次数,取决于递归树,而递归树取决于轴枢的选择。树越平衡,递归次数越少。
而对分区的长短处理顺序,影响的是递归时对栈的使用内存,而不是递归次数
A递归次数和数据排列有关 若有序,这次数为0(N)。理论上最少的次数为0(logN)
BC 每次划分应该先处理较短的分许,只是减少递归占用的内存空间,并不能减少次数
一次划分之后,递归处理前后两段,在处理前一段的时候,当前函数的运行情况要入调用栈。
而处理后一段的时候,原函数的调用栈其实已经没用了,先处理短的先出栈,如果先处理长的,要不停的压栈,浪费内存
参考:http://www.cskaoyan.com/thread-64801-1-1.html
4.对一组数据(2,12,16,88,5,10)进行排序,若前三趟排序结果如下:
第一趟排序结果:2,12,16,5,10,88
第二趟排序结果:2,12,5,10,16,88
第三趟排序结果:2,5,10,12,16,88
则采用的排序方法可能是()。
-
冒泡排序 -
希尔排序 -
归并排序 -
基数排序
解析:
题中所给的三趟排序过程中,每一趟排序是从前往后依次比较,使最大值“沉底”,符合冒泡排序的特点。
提示:对于此类题,先看备选项的排序算法有什么特征,再看题目中的排序过程是否符合这一特征,从而得出答案。一般先从选项中的简单排序方法(插入排序、起泡排序、选择排序)开始判断,若简单排序方法不符合,再判断排序方法(希尔排序、快速排序、堆排序、归并排序)。
5.为实现快速排序算法,待排序序列宜采用的存储方式是()。
-
顺序存储 -
散列存储 -
链式存储 -
索引存储
解析:对绝大部分内部排序而言,只适用于顺序存储结构。快速排序在排序的过程中,既要从后向前查找,也要从前向后查找,因此宜采用顺序存储。 (对绝大部分内部排序而言,只适用于顺序存储结构)
6.已知序列25,13,10,12,9是大根堆,在序列尾部插入新元素18,将其再调整为大根堆,调整过程中元素之间进行的比较次数是()。
-
1 -
2 -
4 -
5
解析:(注意18最后还要和25比较一次)
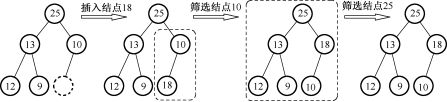
插入18后,首先18与10比较,交换位置,再18与25比较,不交换位置。共比较了2次,调整的过程如下图所示。
7. 在内部排序过程中,对尚未确定最终位置的所有元素进行一遍处理称为一趟排序。下列排序方法中,每一趟排序结束都至少能够确定一个元素最终位置的方法是(A)。
Ⅰ.简单选择排序 Ⅱ.希尔排序 Ⅲ.快速排序
Ⅳ.堆排序 Ⅴ.二路归并排序
-
仅Ⅰ、Ⅲ、Ⅳ -
仅Ⅰ、Ⅲ、Ⅴ -
仅Ⅱ、Ⅲ、Ⅳ -
仅Ⅲ、Ⅳ、Ⅴ
解析:
对于Ⅰ,简单选择排序每次选择未排序列中的最小元素放入其最终位置。对于Ⅱ,希尔排序每次是对划分的子表进行排序,得到局部有序的结果,所以不能保证每一趟排序结束都能确定一个元素的最终位置。对于Ⅲ,快速排序每一趟排序结束后都将枢轴元素放到最终位置。对于Ⅳ,堆排序属于选择排序,每次都将大根堆的根结点与表尾结点交换,确定其最终位置。对于Ⅴ,二路归并排序每趟对子表进行两两归并从而得到若干个局部有序的结果,但无法确定最终位置。
8.对同一待排序序列分别进行折半插入排序和直接插入排序,两者之间可能的不同之处是 ()。
-
排序的总趟数 -
元素的移动次数 -
使用辅助空间的数量 -
元素之间的比较次数
解析:
折半插入排序,是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。 所以,很明显比较的次数减少了
9.对给定的关键字序列110, 119, 007, 911, 114, 120, 122 进行基数排序, 则第 2 趟分配收集后得到的关键字序列是( )。
-
007, 110, 119, 114, 911, 120, 122 -
007, 110, 119, 114, 911, 122, 120 -
007, 110, 911, 114, 119, 120, 122 -
110, 120, 911, 122, 114, 007, 119
解析:C
基数排序是通过“分配”和“收集”过程来实现排序。
1) 首先根据个位数值(只看个位)来排序:
110 120 911 122 114 007 119
2) 再看十位(只看十位数值大小)来排序:
007 110 911 114 119 120 122
3) 最后看百位:
007 110 114 119 120 122
所以 第 2 趟分配收集后得到的关键字序列是 { 007 110 911 114 119 120 122 }。
10.用希尔排序方法对一个数据序列进行排序时,若第1趟排序结果为9,1,4,13,7,8,20,23,15,则该趟排序采用的增量(间隔)可能是 。
-
2 -
3 -
4 -
5
解析:
首先,第二个元素为1,是整个序列中的最小元素,所以可知该希尔排序为从小到大排序。然后考虑增量问题,若增量为2,第1+2个元素4明显比第1个元素9要大,A排除;若增量为3,第i、i+3、i+6个元素都为有序序列(i=1,2,3),符合希尔排序的定义;若增量为4,第1个元素9比第1+4个元素7要大,C排除;若增量为5,第1个元素9比第1+5个元素8要大,D排除,选B。
11.下列选项中,不可能是快速排序第2趟排序结果的是 ()
-
4 14 10 12 8 6 18 -
4 6 10 8 12 14 18 -
6 4 10 8 14 12 18 -
8 4 6 10 12 14 18
解析:每经过一趟快排,轴点元素都必然就位,也就是说,一趟下来至少有1个元素在其最终位置
所以考察各个选项,看有几个元素就位即可。
12.下列排序算法中元素的移动次数和关键字的初始排列次序无关的是(C)
-
直接插入排序 -
起泡排序 -
基数排序 -
快速排序
解析:移动次数和关键字顺序无关的有:
顺口溜:一堆(堆排序)海龟(归并排序)选(选择排序)基(基数排序)友
13.已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次数是() 。
-
1 -
2 -
3 -
4
解析:
将堆画成完全二叉树的形式,堆删除堆顶元素后,是将二叉树最后的叶子节点12放到堆顶,然后将12与其子节点15和10相比较,当15>12时,堆顶12不动,将12与10判断,12>10,不符合小根堆,所以将10和12对调,然后还要将12与其子节点16比较。 所以总共比较3次 疑问:为什么将最后的叶子节点和删除的根节点换
答:
移除根节点后,树就不再是完整的了,数组(这里考虑的是用数组实现堆)中就会有一个空的数据单元,可以把数组中所有的数据都向前移动一个单元,但是这种方法比较慢,所以考虑用最后一个节点填补空的单元,再向下筛选
14.希尔排序的组内排序采用的是 () 。
-
直接插入排序 -
折半插入排序 -
快速排序 -
归并排序
解析:
希尔排序的思想是:先将待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成),分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序
15.对10TB的数据文件进行排序,应使用的方法是 。
-
希尔排序 -
堆排序 -
快速排序 -
归并排序
解析:外部排序指待排序文件较大,内存一次性放不下,需存放在外部介质中。外部排序通常采用归并排序法。选项A、B、C都是内部排序的方法。
详:对于10TB的海量数据,数据不可能一次全部载入内存,传统的排序方法就不适用了,需要用到外排序的方法。外排序采用分治思想,即先对数据分块,对块内数据进行排序,然后采用归并排序的思想进行排序,得到数据的一个有序序列
16.设有6个有序表A、B、C、D、E、F,分别含有10、35、40、50、60和200个数据元素,各表中元素按升序排列。要求通过5次两两合并,将6个表最终合并成1个升序表,并在最坏情况下比较的总次数达到最小。请回答下列问题。
1)给出完整的合并过程,并求出最坏情况下比较的总次数。
2)根据你的合并过程,描述N(N≥2)个不等长升序表的合并策略,并说明理由。
解析:
本题同时对多个知识点进行了综合考查。对有序表进行两两合并考查了归并排序中的Merge()函数;对合并过程的设计考查了哈夫曼树和最佳归并树。外部排序属于大纲新增考点。
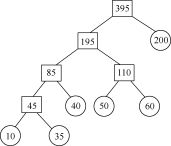
1)对于长度分别为m,n的两个有序表的合并,最坏情况下是一直比较到两个表尾元素,比较次数为m+n-1次。故最坏情况的比较次数依赖于表长,为了缩短总的比较次数,根据哈夫曼树(最佳归并树)思想的启发,可采用如图所示的合并顺序。
根据上图中的哈夫曼树,6个序列的合并过程为:
第1次合并:表A与表B合并,生成含有45个元素的表AB;
第2次合并:表AB与表C合并,生成含有85个元素的表ABC;
第3次合并:表D与表E合并,生成含有110个元素的表DE;
第4次合并:表ABC与表DE合并,生成含有195个元素的表ABCDE;
第5次合并:表ABCDE与表F合并,生成含有395个元素的最终表。
由上述分析可知,最坏情况下的比较次数为:第1次合并,最多比较次数=10+35-1=44;第2次合并,最多比较次数=45+40-1=84;第3次合并,最多比较次数=50+60-1=109;第4次合并,最多比较次数=85+110-1=194;第5次合并,最多比较次数=195+200-1=394。
故比较的总次数最多为:44+84+109+194+394=825。
2)各表的合并策略是:在对多个有序表进行两两合并时,若表长不同,则最坏情况下总的比较次数依赖于表的合并次序。可以借用哈夫曼树的构造思想,依次选择最短的两个表
进行合并,可以获得最坏情况下最佳的合并效率。
【1)2)评分说明】①对于用类似哈夫曼树(或最佳归并树)思想进行合并,过程描述正确,给5分。按其他策略进行合并,过程描述正确,给3分。
② 正确算出与合并过程一致的总比较次数,给2分。若计算过程正确,但结果错误,可给1分。
③ 考生只要说明采用的是类似哈夫曼树(或最佳归并树)的构造方法作为合并策略,即可给3分。如果采用其他策略,只要能够完成合并,给2分。