剑指offer（19-24）题解

19题解–顺时针打印矩阵

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

思路解析

这题就属于是那种看起来贼简单，实现起来要命的题，之前自己就碰到这道题，当时就没做出来，这次还是没做出来。其实思想就是不断的减少整个矩阵的范围，就如下图所示：

重点是我们如何来确定边界，以及边界值的变化

源代码

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printMatrix(int [][] matrix) {
         ArrayList<Integer>list=new ArrayList<Integer>();
         if(matrix==null||matrix.length==0||matrix[0].length==0)
                   return list;
         int up=0;
         int down=matrix.length;
         int left=0;
         int right=matrix[0].length;
         while(true)
         {
             //取上边界
             for(int i=left;i<right;i++)
                 list.add(matrix[up][i]);
             //下调上边界
             up++;
             //检查是否越界
             if(up>=down)
                 break;
             //取右边界
             for(int i=up;i<down;i++)
                 list.add(matrix[i][right-1]);
             //下调右边界
             right--;
             //检查是否越界
             if(right<=left)
                 break;
             //取下边界
             for(int i=right-1;i>left-1;i--)
                 list.add(matrix[down-1][i]);
             //上调下边界
             down--;
             //检查是否越界
             if(down<=up)
                 break;
             //取左边界元素
             for(int i=down-1;i>up-1;i--)
                 list.add(matrix[i][left]);
             //上调左边界
             left++;
             //检查是否越界
             if(left>=right)
                 break;
         }
         return list;
        }
}

20题解–包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

思路解析

一开始博主的想法就是通过两个栈，在元素入栈的过程中就通过两个栈来实现排序将栈内元素按照降序排列，但是测试之后发现是不可以的，因为题目中要求的是在O(1)的时间复杂度内完成，所以我们是不能通过这种方法实现的。
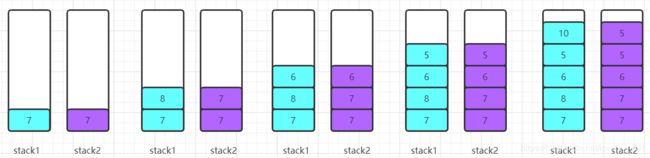
这里我们选择的还是通过两个栈来实现，但是一个栈只存储我们的入栈元素，另一个栈就存储相应入栈区间内的最小元素，我们通过下面的图来模拟一下，大家就知道了。
假设我们的入栈元素是这样的：{7,8,6,5,10}

只要注意在进行pop操作时，需要将两个栈的栈顶元素同时pop.

源代码

import java.util.Stack;

public class Solution {
    Stack<Integer>stack1=new Stack<Integer>();
	Stack<Integer>stack2=new Stack<Integer>();
	public void push(int node) {
		if(stack1.isEmpty())
		{
			stack1.push(node);
			stack2.push(node);
		}
		else {
		//stack2始终存入区间内最小的元素
			if(node<stack2.peek()) 
				stack2.push(node);
			else 
				stack2.push(stack2.peek());
			stack1.push(node);
		}
	}
   //两个栈都需要进行pop操作
    public void pop() {
    	stack1.pop();
    	stack2.pop();
    }
    
    public int top() {
    	return stack2.peek();
    }
    
    public int min() {
    	return top();
    }
}

21题解–栈的压入，弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

思路解析

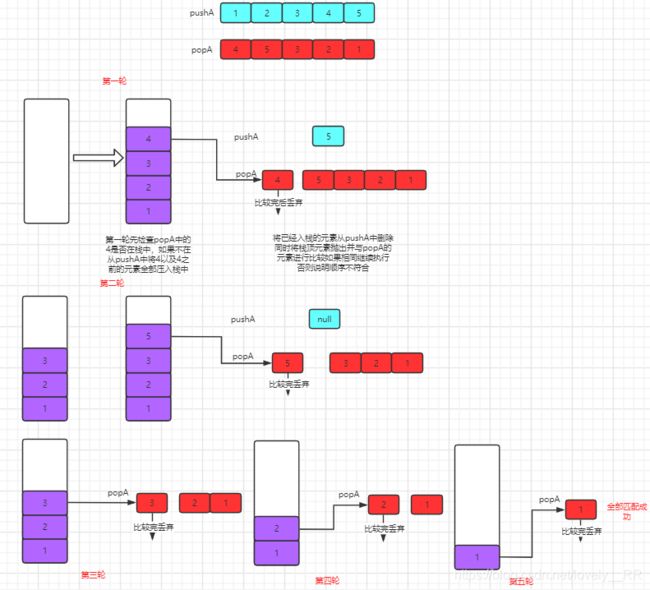
这题我的主要思路就是通过popA数组的元素来确定那些元素已经入栈了，只要确定好那些元素已经入栈了，那么这些元素的相对位置就是固定的，举个例子：
pushA=[1,2,3,4,5],popA=[4,3,5,1,2]
既然先pop 4，再根据pushA可知,1,2,3,4必定已经全部入栈了，所以4,3,2,1的出栈的相对位置已经定下来了，所以当前的出栈顺序一定是不满足的。

之后再通过图解来演示一遍代码的过程。

源代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Stack;
public class Solution {
    Stack<Integer>stack=new Stack<Integer>();
	 public boolean IsPopOrder(int [] pushA,int [] popA) {
		 ArrayList<Integer>list1=new ArrayList<Integer>();
		 ArrayList<Integer>list2=new ArrayList<Integer>();
		 for(int i=0;i<pushA.length;i++)
			 list1.add(pushA[i]);
		 for(int i=0;i<popA.length;i++)
			 list2.add(popA[i]);
		 Arrays.sort(pushA);
		 Arrays.sort(popA);
		 //首先两个数组中的元素一定要一直，否则一定不可能
		 if(!Arrays.equals(pushA, popA))
			 return false;
		 for(int i=0;i<list2.size();i++)
		 {
		     //如果出现栈中不存在该元素，说明该元素还未入栈，
		     //所以我们便将他以及他入栈之前的元素一同入栈
			 if(!stack.contains(list2.get(i)))
			 {
				 int j=0;
				 while(list1.get(j)!=list2.get(i))
				 {
					 stack.push(list1.get(j));
					 j++;
				 }
				 stack.push(list1.get(j));
				 //入栈之后也不要忘记将list中这些已经入栈的元素删掉，否则会造成重复
				 for(int k=0;k<j+1;k++)
					 list1.remove(0);
			 }
			 //比较出栈的元素是否与popA的出栈元素相同，如果不同说明不符合
			 if(stack.pop()!=list2.get(i))
				 return false;
		 }
		 return true;
	    }
}

22题解–从上往下打印二叉树

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

思路解析

这和之前我博客中一条题目是类似的，其实也是按照下面图的流程做的

只不过这里不需要分层打印，所以不需要再次计数。

源代码

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
     public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
		 ArrayList<Integer>list=new ArrayList<Integer>();
		 Queue<TreeNode>queue=new LinkedList<TreeNode>();
		 if(root==null)
			 return list;
		 else 
		 {
			 queue.add(root);
			 while(!queue.isEmpty())
			 {
				 TreeNode node=queue.poll();
				 list.add(node.val);
				 if(node.left!=null)
					 queue.offer(node.left);
				 if(node.right!=null)
					 queue.offer(node.right);
				 
			 }
			 return list;   
		 }
	    }
}

23题解–二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

思路解析

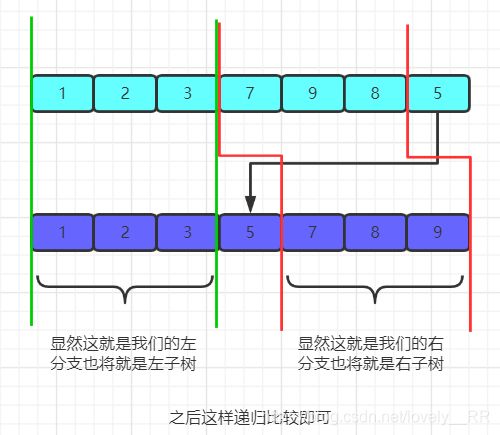
二叉搜索树有一个性质就是，二叉搜索树的中序遍历序列是一个升序序列，所以我们可以通过题目给我们的后续序列，将它排序过后构成我们的中序序列，有了中序序列以及后续序列显然我们就可以将这棵二叉树还原出来，如果能够还原那么该后续序列就是可以，否则不行。
还是通过下面的图来进行讲解
假设我们的后序序列是[1,2,3,7,9,8,5]
显然我们能得到中序序列[1,2,3,5,7,8,9]

源代码

import java.util.ArrayList;
import java.util.Arrays;
public class Solution {
  //比较这两个数组中元素是否一致
  public boolean panduan(int []num1,int []num2)
	{
		ArrayList<Integer>list=new ArrayList<Integer>();
		for(int i=0;i<num2.length;i++)
			list.add(num2[i]);
		for(int i=0;i<num1.length;i++)
		{
			if(!list.contains(num1[i]))
				return false;
		}
		return true;
	}
	public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence.length==0)
			return false;
		int []num=new int [sequence.length];
		for(int i=0;i<num.length;i++)
			num[i]=sequence[i];
		//构造中序序列
		Arrays.sort(sequence);
		for(int i=0;i<sequence.length;i++)
		{
			if(sequence[i]==num[num.length-1])
			{
			    //后序序列的左分支即左子树
				int []left=Arrays.copyOfRange(sequence, 0, i);
				//后序序列的右分支即右子树
				int []right=Arrays.copyOfRange(sequence, i+1, num.length);
				//比较中序及后序的左分支元素是否相同
				if(!panduan(left, Arrays.copyOfRange(num, 0, i)))
					return false;
				//比较中序及后序的右分支元素是否相同
				if(!panduan(right, Arrays.copyOfRange(num, i, num.length-1)))
					return false;
				//递归检查左分支的左右分支
				VerifySquenceOfBST(Arrays.copyOfRange(num, 0, i));
				//递归检查右分支的左右分支
				VerifySquenceOfBST(Arrays.copyOfRange(num, i, num.length-1));
			}
		}
        return true;
    }
}

24题解–二叉树中和为某一值的路径

题目描述

输入一颗二叉树的根节点和一个整数，按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

思路解析

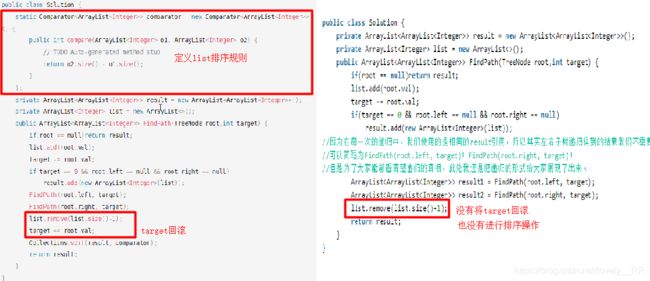
这题主要用的是搜索，但是因为自己好久没写过搜索了，所以这题就没想出来，这题是看的别人的题解，但是那位大佬的题解有点问题，首先他只对list进行了回滚，但是没有对target的值进行回滚，并且也没有对整个序列进行字典排序，但是他的代码竟然是过了的，说明牛客的案例还是不太严谨，这里我贴出不一样的地方，大家可以比较一下。

源代码

import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    public TreeNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    static Comparator<ArrayList<Integer>> comparator = new Comparator<ArrayList<Integer>>() {
		public int compare(ArrayList<Integer> o1, ArrayList<Integer> o2) {
			// TODO Auto-generated method stub
			return o2.size() - o1.size();
		}
	};
    private ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
    private ArrayList<Integer> list = new ArrayList<>();
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        if(root == null)return result;
        list.add(root.val);
        target -= root.val;
        if(target == 0 && root.left == null && root.right == null)
            result.add(new ArrayList<Integer>(list));
        FindPath(root.left, target);
        FindPath(root.right, target);
        list.remove(list.size()-1);
        target += root.val;
        Collections.sort(result, comparator);
        return result;
    }
}

看到最后了如果可以的话可以关注一下博主的b站号，新人up需要你的支持。