java数据结构源码解读——TreeMap红黑树
“手写一棵红黑树”是程序员之间常用的调侃。为何呢?红黑树说是一颗“二叉树”,但实际上操作的难度(插入/删除)远远高于普通的二叉搜索树,也高于AVL树。
工业上(java库/cpp stl)使用红黑树作为树结构自然也是有它的考虑的。
据有些书上和博客上说:
AVL树的插入/删除极端条件下可能比红黑树慢很多;(因为涉及多次旋转操作,而红黑树只需要三次)
AVL树平衡性是追求近乎绝对的平衡,所以搜索速度略快于红黑树;(红黑树不够平衡)
这篇博客主要是查看一下底层的代码,并且复习一下红黑树的知识(等会我算法导论哪去了。。)
在看代码之前,我们需要复习一下红黑树的定义:
1、每个节点的颜色要么是红色,要么是黑色。
2、根节点是黑色的。
3、叶节点是黑色的。
4、如果一个节点是红色,那么他的两个子节点都是黑色。
5、对于每个节点,从该节点到后代叶节点的路径上,都包含相同数目的黑色节点。
接下来看代码吧。
首先是字段:
private final Comparator comparator;//定义的比较器
private transient Entry root;//根节点
private transient int size = 0;//节点数
private transient int modCount = 0;//防止并发修改 构造器略,十分简单。初始的根节点就是一个null。
下面是键值对(节点)的定义:
static final class Entry implements Map.Entry {
K key;
V value;
Entry left;
Entry right;
Entry parent;
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
Entry(K key, V value, Entry parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry e = (Map.Entry)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
} 新建的节点为黑色,并且有父节点,两个子节点的引用。
在这里我们不会提到搜索操作,因为实在是太简单,无论是递归还是非递归,无论是否使用比较器还是自带操作符。
重点我们观察它的插入、删除。
public V put(K key, V value) {
Entry t = root;
if (t == null) {
compare(key, key); // type (and possibly null) check
//空值情况,直接插入一个新节点并返回null
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
// split comparator and comparable paths
Comparator cpr = comparator;
if (cpr != null) {
do {//比较器非空,使用比较器进行比较
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
do {//比较器为空的情况
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
Entry e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//插入完毕后对路径上的节点进行修复,可能进行旋转、变色之类的操作
fixAfterInsertion(e);
size++;
modCount++;
return null;
} 这一堆函数啰嗦了这么多实际上只做了一件事,按路径搜索,如果找到key相等的就更新value,否则就插入一个节点。
parent指针在搜索的迭代过程中是当前指针的父节点,只为把一个新节点插入到一个空位置。
插入之后自然是要对这个树进行修复的,否则,也不叫红黑树了。
所以fixAfterInsertion方法格外重要。
private void fixAfterInsertion(Entry x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
脑袋疼吗!我也脑袋疼。这么多东西看得人头大,首先看几个里面比较简单的方法,这些方法是修复操作的不可缺少的部分。
private static Entry parentOf(Entry p) {
//找到父节点,如果为空则返回空
return (p == null ? null: p.parent);
}
private static Entry leftOf(Entry p) {
//找到左孩子,如果为空则返回空
return (p == null) ? null: p.left;
}
private static Entry rightOf(Entry p) {
//找到右孩子,同上
return (p == null) ? null: p.right;
}
private static void setColor(Entry p, boolean c) {
if (p != null)//为非空节点修改颜色
p.color = c;
}
private static boolean colorOf(Entry p) {
return (p == null ? BLACK : p.color);//返回节点颜色,记住最底层的叶子节点(空的)是黑色
} 显然,修改颜色重置颜色并不能从根本上改变红黑树的平衡性,平衡性的维护应当和AVL树一样,是旋转。
private void rotateLeft(Entry p) {
if (p != null) {
Entry r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
private void rotateRight(Entry p) {
if (p != null) {
Entry l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
} 这两个是左旋转和右旋转函数,接下来我会以图说明:
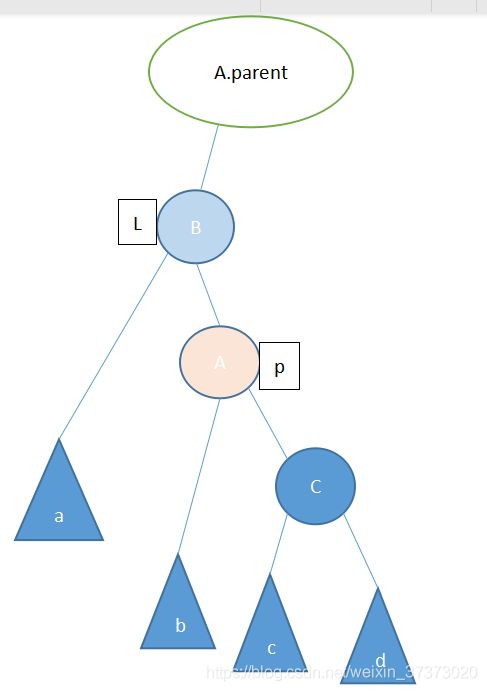
首先是“右旋转”:
先记住这张图——B、C分别是A的左右孩子,abcd是孙子辈的子树,子树可能是空,也可能不是。
我们直接看一般情况:
哎你懂了吧,这个就是AVl树里面的旋转啊。看不懂的可以拿纸自己手画一下。
好了,那么其实左旋转几乎是一样的,就是一个相对来说对称的操作。
好了知道这俩旋转是干什么用的,就来看看修复平衡的函数:
首先看前一个函数的最后一段代码:
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);说明现在开始从插入的节点向上修复:
private void fixAfterInsertion(Entry x) {
x.color = RED;//先把待修复的节点设为红色
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//如果x的父节点是父节点的父节点的左节点(说白了,x父节点是作为左孩子)
Entry y = rightOf(parentOf(parentOf(x)));//y是祖父的右孩子,是x的叔节点
//《算法导论》中情况一
//需要重新把父、叔染黑(因为不能两个红色做父子)
//这时候进入情况二
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
//情况二,叔是黑色,父子红色,需要左旋转
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
//情况三,最后保持平衡,右旋转
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
//与上一个对称的方法
Entry y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;//根节点永远是黑色
} 经过这么一看,实际上不算左右对称的判断,插入时的修复有三种情况。
删除是有四种情况的判断,依旧是修复五条规则。这里暂且不表,等有时间了,自己实现一个。