OO第一单元总结
程序结构
第一次作业
第一次作业比较简单,只涉及幂函数的加减,因此我采用小正则对每一项进行识别并存入HashMap中,在此次作业中主类承担了包括对输入进行处理,项的识别,同类项合并,输出等功能,比较臃肿。
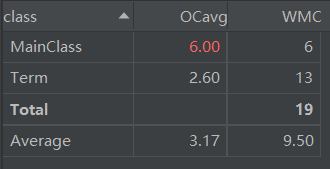
复杂度分析如下:
第一次作业有一个bug和一个与性能有关的小问题:
Bug是由于对空的HashMap的判断的顺序在输出的后面,因此当求导结果为0时会报错。与性能有关的小问题时当有类似的求导结果时仍然会输出。
第二次作业
第二次作业新增加了对于WF和三角函数的支持,在WF的判断方面我选择使用一个大正则来匹配一整个表达式,同时将对输入的处理由主类交到专门的类中。
对于表达式中项的匹配,仍然采用小正则对于每一个因子进行匹配。同时将每一项固定的化简为
C×x^xPower×〖sin(x)〗^sinPower×〖cos(x)〗^cosPower
之后运用公式进行求导。在优化环节,由于我的能力有限,因此仅仅合并了同类项,没有做更多的优化。
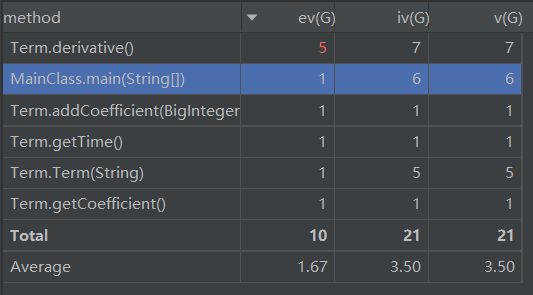
代码复杂度分析如下:
第二次作业中出现了三个bug:
第一个bug是审题不清造成的对WF的错判,我将对幂函数指数的检查放在了因子合并之后,而实际上应该是对于每一个因子单独判断。
第二个bug是关于空白字符的问题,我在忽略空白字符时使用了正则表达式中的\\s,然而实际空白字符只有空格和制表符,因此漏掉了一些不合法的空白字符。
第三个bug是关于符号化简的,我对于所有的符号先化简++或--再化简+-或-+,这就导致了以类似-+-开头的项的符号会出现错误。
第三次作业
我个人认为第三次作业最大的难度就在于添加了多项式因子这一项,也正是这样一个迭代运算的出现使得我不得不对代码进行重构。
但是重构时我漏看了题目中的一句话,误认为表达式因子只会出现在三角函数中,因此最终中测有两个点没有通过,强测也仅仅通过了WF的测试点。
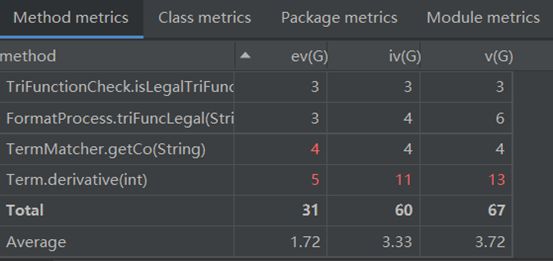
代码复杂度如下:
由于代码结构的整体性错误,因此谈bug意义不大。
寻找他人bug的策略
主要用手动构造边缘数据的方法来测试bug,同时也会随机构造一至两个随机表达式,通过对其的求导不断迭代得到新的表达式。同时,也通过阅读其他同学的源代码,发现了一个优化相关的bug。
应用对象创建模式进行重构
在三次作业中,我的关于项的类都只有一种,只是类中封装的数据不同。如果要对代码进行重构,应该将项作为一个抽象类,所以具体的项(包括幂函数项,三角函数项,表达式项等)都继承自该抽象类,然后使用工厂模式而不是构造方法来创建具体对象。这样可以使得代码的可扩展性更好,同时还能避免当具体项种类越来越多时封装数据过多的问题。
心得和体会
关于面向对象:在我这一单元的代码中,仍然保留着许多面向过程编程的部分。在三次作业中没有使用接口和继承,仅仅是调用对象的方法来处理数据。
关于测试:自己在手动构造测试数据时往往难以发现自己的错误,还是需要与其他同学交换测试数据以及使用自动化评测机。
关于重构:在刚开始的时候没有考虑到代码的可扩展性,仅仅考虑了对于当前需求的满足,导致在第三次作业时需要对整个代码进行重构。
关于正则表达式:对于大正则的构造,使用和修改都十分痛苦,需要避免。