BP神经网络——如何进行权值的初始化
如果以面向对象(OOP)的方式进行BP神经网络系统的设计与实践的话,因为权值的初始化以及类的构造都只进行一次(而且发生在整个流程的开始阶段),所以自然地将权值(全部层layer之间的全部权值)初始化的过程放在类的构函数中,而权值的初始化,一种trivial常用的初始化方法为,对各个权值使用均值为0方差为1的正态分布(也即np.random.randn(shape))进行初始化,也即:
class Network(object):
# topology:表示神经网络拓扑结构,用list或者tuple来实现,
# 比如[784, 30, 10],表示784个神经元的输入层,30个neuron的隐层,以及十个neuron的输出层
def __init__(self, topology):
self.topology = topology
self.num_layers = len(topology)
self.biases = [np.random.randn(y, 1) for y in topology[1:]]
self.weights = [np.random.randn(y, x) for x, y in zip(self.weights[:-1], self.weights[1:])]我们不妨以一个简单的具体例子,分析这种初始化方法可能存在的缺陷,如下图所示:
为了简化问题,我们只以最左一层向中间一层的第一个神经元(neuron)进行前向(forward)传递为例进行分析,假设一个输入样本(特征向量, x ,维度为1000),一半为1,一半为0(这样的假设很特殊,但也很能说明问题),根据前向传递公式, z=∑jwjxj+b , z 即为输入层向中间隐层第一个神经元的输入。因为输入的一半为0的缘故,再根据前文以及代码也即权重和偏置初始化为独立同分布的 标准高斯随机变量, z 为501(500个权值+1个偏置)个标准正太随机变量的和,由 独立随机变量和的方差等于方差的和可知,因此 z 的分布服从0均值,标准差为 501−−−√≈22.4 ,标准差从1升高到22.4,由高斯密度函数 f(x)=12π√σexp(−(x−μ)2σ2) 可知,方差越大,密度函数的分布越扁平,也即分布越均匀而不是集中在一段区域,其概率密度函数为(可见十分平坦):
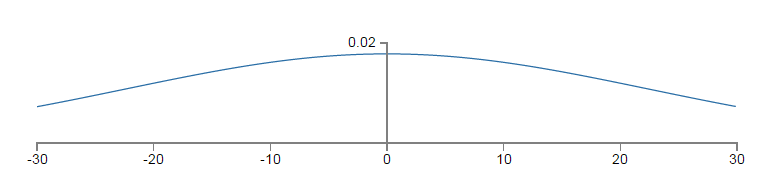
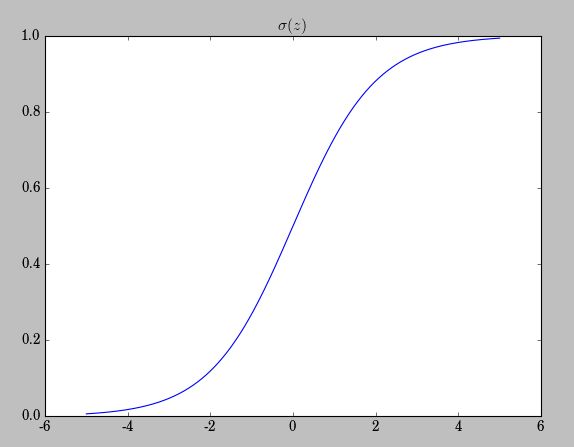
以上的平坦的概率密度函数为 z 的pdf(概率密度函数),因为pdf较为均匀, |z| 的值就不会像 N∼(0,1) 那样集中于均值附近(越远离均值中心,密度值会迅速衰减),而会以更大的概率取更大的值。这中初始化机制可能带来什么样的问题呢? |z| 取值很大,也即 z≫1 或者 z≪−1 ,相应的该神经元的activation值 σ(z) 就会接近0或者1,而我们知道,如下图示, σ(z) 越靠近0或者1其变化率越小,也即是达到一种饱和(saturate)状态。
而权值更新公式为:
也就意味着越小的 σ′(z) ,越小的梯度更新,同等学习率(learning rate: η )的情况下,越小的学习速率。
如何进行改进呢?假使输入层有 nin 个神经元,我们可将这些神经元对应的权重初始化为0均值,标准差为 1/(√nin) ,这样,高斯pdf的形式将会趋于陡峭,而不是上文的平坦, σ′(z) 将以较小的概率达到饱和状态。仍以上文的设置为基础,我们来分析,现在 z 的pdf,均值为0,标准差为 500/1000−−−−−−−−√≈0.707 ,其形式如下:
相关代码:
def default_weight_init(self):
self.biases = [np.random.randn(y, 1)/y for y in self.topology[1:]]
self.weights = [np.random.rand(y, x)/np.sqrt(x) for x, y in zip(self.topology[:-1], self.topology[1:])]
def large_weight_init(self):
self.biases = [np.random.randn(y, 1) for y in self.topoloy[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.topology[:-1], self.topology[1:])]我们看到正是这样一种np.random.randn(y, x)向np.random.randn(y, x)/np.sqrt(x)小小的改变,却暗含着丰富的概率论与数理统计的知识,可见无时无刻无处不体现着数学工具的强大。