一、代码分析
第一次作业
思路
第一次作业作为多项式求导这个作业系列来说,难度并不是很高。只需要考虑简单的带系数的幂函数的加减。
我在设计程序时将程序分成了三个部分,多项式的读取,多项式的求导,多项式的输出。之后的作业也是按照这样的结构进行设计。
读取部分:整个多项式字符串是由多个项字符串拼接起来的,并且项的格式固定,输入数据也不存在错误格式的数据,因此考虑采用正则表达式循环匹配输入字符串中符合项格式的子字符串,并按照项的格式读取系数和指数。对于多项式的存储,我采用了TreeMap来存储多项式,使用<指数:项>这样一个键值对来存取,在读取原多项式的过程中就进行同类项的合并,合并过程中出现的零系数项直接去除。
求导部分:幂函数的求导方法简单,对于多项式中存储的每一项,返回一个求导后的项,在将这些求导后的项放到新的多项式中。
输出部分:系数为1或-1直接忽略数字,指数为0按常数输出,指数为1忽略指数。输出时按照降幂输出。
性能部分:第一次作业的性能分,只需要考虑项系数指数的特殊情况、多项式尽可能以正项开头、合并同类项就可以拿高分。
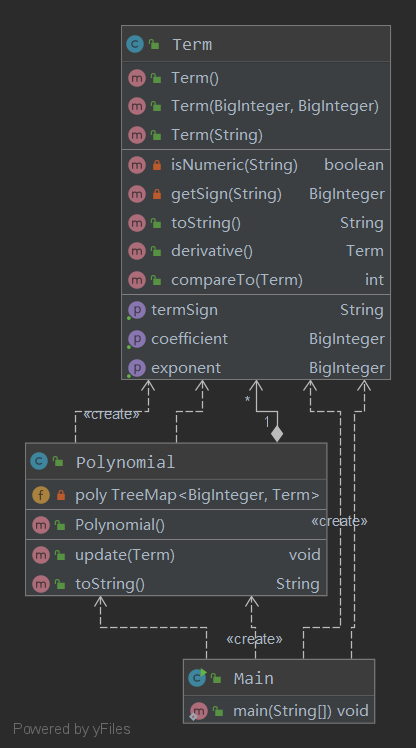
类图
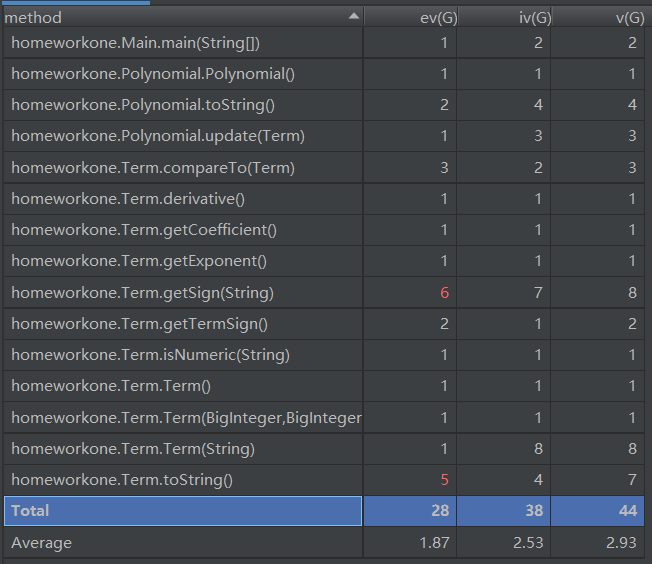
Metrics
分析
本次作业的难度不高,由于是第一次作业,我的程序在整体上并没有很好的遵从面向对象的思想。通过Metrics进行分析,我的程序在输出的toString函数上基本复杂度较高,主要是因为该方法中含有大量的if语句对项的输出进行特判,还需要进一步改进。
第二次作业
思路
第二次作业相较于第一次作业增加了三角函数sin(x) cos(x),增加了因子的种类,但由于三角函数内部没有嵌套,所以格式固定,因此第二次作业的多项式读入仍然可以采用正则表达式逐项读入分析的方法。经过一个星期的学习和观摩其他同学的优秀作业,我从程序结构入手对第二次作业的代码进行了一次重构。
重构后的代码将作业中需要的功能进行分析和结构,并将这些功能按照类型整理到不同的包中,对于存储多项式的数据结构,则抛弃第一次作业中将分析项的代码放在项的构造函数中的方法,设置分析多项式、项和因子的三个工厂方法。
读取部分:依旧是之前的正则划分项,然后逐项读入,但是由于第二次作业中增加了对表达式格式错误的判定,因此利用异常机制来进行处理,在分析项的工厂方法中设置白名单机制,对符合白名单的项进行处理并返回相应的项,否则抛出异常。利用,依旧在读取过程中进行同类项的合并。多项式采用Hash Map这一数据结构来存储,为方便化简,设置<指数三元组 : 项>的映射关系。
求导部分:本次作业的每一项都可以看作是系数、sin、cos、幂函数的乘积,具有如下形式:
因此采用统一的公式对其进行求导,一项求导变三项,分别存进新的多项式。
输出部分:沿袭上次的输出策略,采用先特判,否则正常输出的策略。
性能:本次性能分较难获取,主要是要考虑同类项的合并,项的精简输出,以及三角恒等式的应用。
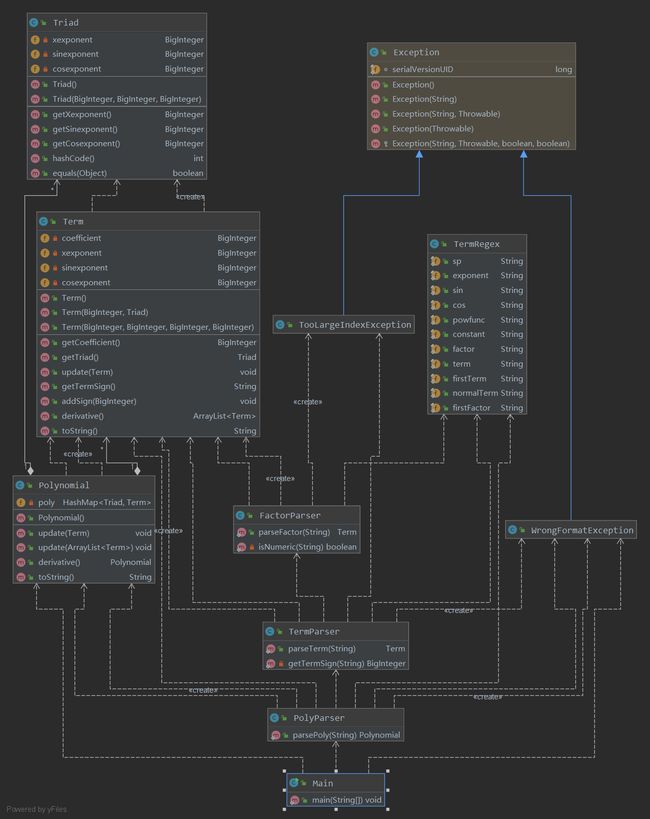
类图
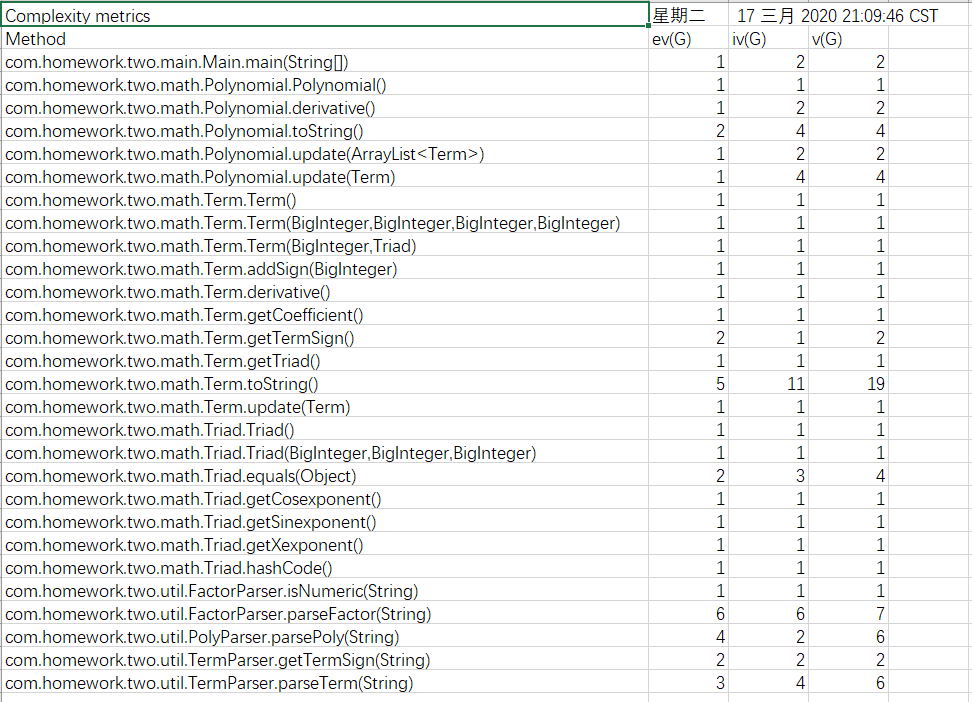
Metrics
分析
本次作业相较于上一次作业相比,难度没有太大的提升,新增因子形式的固定使得正则表达式按项读取的方法依旧可用,改动主要集中在代码整体框架和求导方式的改变上。通过Metrics工具分析,这次代码的表达式输出部分,逻辑较为复杂,耦合度高,还需要作进一步的改进。
第三次作业
思路
第三次作业的难度较前两次的作业有了一个大幅度的提升,原因在于引入了三角函数的嵌套和表达式因子,嵌套的存在引入了大量的括号,而表达式因子的存在使得按照正则表达式读入的方法变得不太现实,与此同时,统一项的格式也变得困难,这就使得之前统一项的求导公式也变得不可能,所以这次作业需要对存储多项式的数据结构进行一次大的调整。这次作业的代码结构依旧采取的式第二次作业的代码结构,主要改动集中于项的存储和求导部分。
读取部分:根据多项式中括号的一一对应关系,我采用了根据括号深度和加减号来分项的方法,设置一个输入字符串的标记,每次遇到左括号标记加一,遇到右括号标记减一,标记为零时才能根据加减号进行分项,这样就杜绝了正则表达式匹配时的问题。对拆开的每一项,根据乘号和括号深度进行因子的拆分,再分析每一个因子。对于表达式因子,在去除括号后当作多项式进行递归分析,由于表达式长度的有限性,递归具有出口。对多项式的存储,按照多项式、项、因子的层次进行存储,采用ArrayList容器进行存储。因子层面,设置一个抽象因子类,并通过继承该因子类生成本次作业需要的常数因子、三角函数因子、幂函数因子和表达式因子。对错误格式的判别仍然使用第二次作业的白名单机制。
求导部分:为因子类实现一个求导接口,并返回求导后得到的因子。
输出部分:沿用第二次作业输出的策略。
性能:本次作业需要考虑的是同类项的合并,同类因子的合并,多层括号嵌套的化简。我在本次作业中完成了同类因子的合并和多层括号的化简两部分。
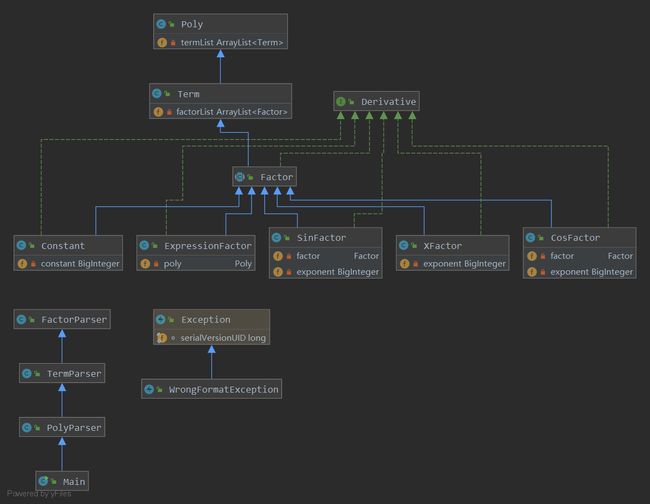
类图
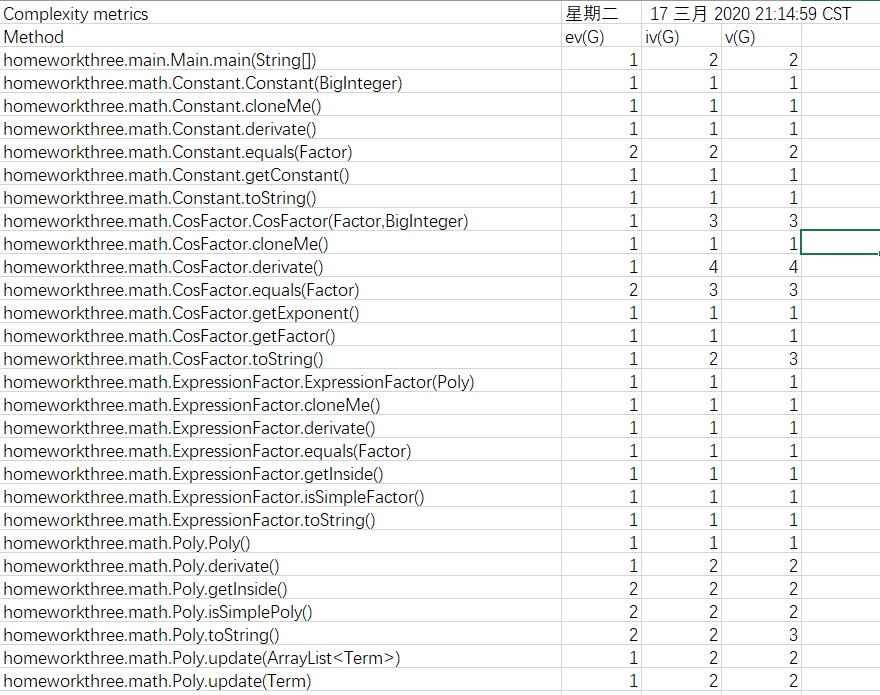
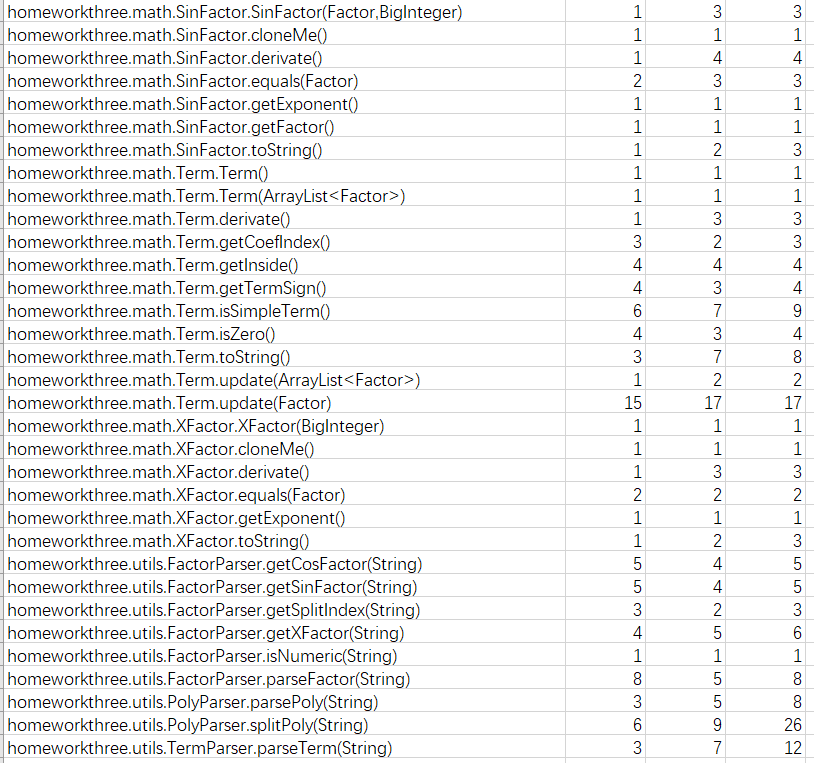
Metrics
分析
本次作业是这一系列中最难的一次作业,嵌套因子的存在提高了设计代码是的复杂度,因此要采用递归结构来存储。通过Metrics工具进行分析,本次代码中对项的增加因子、分析因子和划分项的方法较为复杂,需要进一步的处理简化。
BUG分析
第一次作业
中强测部分:未出现bug
互测部分:发现了一个给常数求导后没有输出的bug,经过检查,错误发生在项的toString函数中。
第二次作业
中强测部分:未出现bug
互测部分:未出现bug
第三次作业
中强测部分:未出现bug
互测部分:发现了一个在判定因子是否相同时缺少了判定条件的bug,例如会把sin(123)和sin(12)看作相同的因子,把sin(x)和sin(x)**2看成相同的因子,经过检查,错误发生在常数类、三角函数类中的equals方法中。
互测策略
互测中,我的方法主要有两类,第一类是覆盖性测试,通过python中的工具库生成一系列数据进行广撒网处理。第二类是定点爆破,阅读同学的代码,分析其中的漏洞,从求导作业的结构出发,针对每个结构构造对应的数据。
互测中发现的bug
第一次作业:合并同类项导致输出为空
x**2-x**2
第二次作业:错误格式的误判
x**10000
第三次作业:递归过深导致的超时
((((((((((((((((((((((x))))))))))))))))))))))
应用对象创建模式
第一次作业直接使用构造方法分析字符串来生成项,并不是一种好方法。应该将业务逻辑移动到工厂类当中,减少Term类、Poly类、Factor类的体量。
第二、三次作业使用了简单工厂模式,构造parsePoly、parseTerm、parseFactor方法来进行字符串的处理,并返回相应的实例。
心得体会
做完OO课程的第一个系列的作业,我觉得我的收获还是很多的。
1.清晰的代码框架。我在做第一次作业的时候,并没有很好的利用JAVA语言作为一门面向对象语言的特点,整个代码结构还是过于面向过程化,函数化,能够体现出结构化特点,但不能体现出高内聚低耦合的特点。在后面的两次作业中,我尝试着学习和借鉴一些优秀代码的框架和编码风格,来完成代码的编写。
2.代码的模块化调试。回顾这三次作业中我的代码编写流程,大致的流程实际是一致的,都是在将作业要求分解成几个小的模块之后进行每个模块的编码和调试,完成一个模块的编写后再进行下个模块的编写。后来了解到这种模式叫做单元测试。这种方法也避免了一次写完代码之后可能会出现的难以定位bug的问题。
3.迭代开发的优点。这三次作业需求不断提高,但是这些提高都是再前一次作业的基础上完成的,所以如果不能进行迭代式的开发,就会增加很多不必要的代码量,而迭代开发的基础是要拥有一个良好的代码框架。但事实上我在这方面做的并不是很好,在每次作业中,代码还是进行了比较大幅度的改动。
4.学会利用网络资源。历次作业的完成,我都是先通过在网上查找相关的资料,阅读讨论区中大佬的一些思路,在比较和借鉴中形成自己的思路,再完成代码的编写。此外,对JAVA编程中一些不熟悉的类或者方法,从网络上获取相关的教程也十分的方便和快捷。
5.面向对象的思想和应用。作为OO课程的核心内容,这三次作业的难度不断增加,但通过三次作业的历练,我也逐渐掌握了一些面向对象编程的基本方法和思想,并运用到了作业当中。