初级算法学习day2

1、逻辑回归与线性回归的联系与区别
联系：两种都可以归于同一个家族，即广义线性模型。这个家族中的模型形式基本上都差不多，不过的是因变量不同，如果是连续的就是多重线性回归，如果是二项分布就是logistic回归。
区别：
（1）线性回归用来预测，逻辑回归用来分类；
（2）线性回归是拟合函数，逻辑回归是预测函数；
（3）线性回归的参数计算方法是最小二乘法，逻辑回归的参数计算方法是梯度下降

2、逻辑回归的原理
（1）找一个合适的预测函数（Andrew Ng的公开课中称为hypothesis），一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程时非常关键的，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数。
（2）构造一个Cost函数（损失函数），该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。
（3）显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有的是梯度下降法（Gradient Descent）。

3、逻辑回归损失函数推导及优化
回顾下线性回归的损失函数，由于线性回归是连续的，所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的，自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然法来推导出我们的损失函数。
参考链接

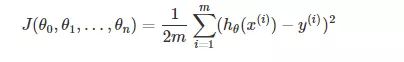
4、正则化与模型评估指标
（1）过拟合问题
过拟合即是过分拟合了训练数据，使得模型的复杂度提高，泛化能力较差。
（2）过拟合主要原因
过拟合问题往往源自于过多的特征
解决方法
1）减少特征数量
2）正则化
（3）正则化方法
正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化项就越大。常见的有L1正则化和L2正则化。
逻辑回归的L1正则化的损失函数表达式如下，相比普通的逻辑回归损失函数，增加了L1的范数做作为惩罚，超参数α作为惩罚系数，调节惩罚项的大小。

J(θ)=−YT∙loghθ(X)−(E−Y)T∙log(E−hθ(X))+α||θ||1

其中||θ||1为θ的L1范数，逻辑回归的L1正则化损失函数的优化方法常用的有坐标轴下降法和最小角回归法。
二元逻辑回归的L2正则化损失函数表达式如下

J(θ)=−YT∙loghθ(X)−(E−Y)T∙log(E−hθ(X))+12α||θ||22

其中||θ||2为θ的L2范数，逻辑回归的L2正则化损失函数的优化方法和普通的逻辑回归类似。

5、逻辑回归的优缺点
优点：
（1）预测结果是界于0和1之间的概率
（2）可以适用于连续性和类别性自变量
（3）容易使用和解释
缺点：
（1）对模型中自变量多重共线性较为敏感，例如两个高度相关自变量同时放入模型，可能导致较弱的一个自变量回归符号不符合预期，符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量，以减少候选变量之间的相关性
（2）预测结果呈“S”型，因此从log(odds)向概率转化的过程是非线性的，在两端随着log(odds)值的变化，概率变化很小，边际值太小，slope太小，而中间概率的变化很大，很敏感。 导致很多区间的变量变化对目标概率的影响没有区分度，无法确定阀值

6、样本不均衡问题解决方法
（1）扩大数据集
（2）尝试增加其他评价指标F1/Recall/Kappa/ROC
（3）重采样
（4）其他分类模型
（5）增加惩罚项

7、sklearn参数

class sklearn.linear_model.LogisticRegression(
    penalty=’l2’, 参数类型：str，可选：‘l1’ or ‘l2’, 默认: ‘l2’。该参数用于确定惩罚项的范数
    dual=False, 参数类型：bool,默认：False。双重或原始公式。使用liblinear优化器，双重公式仅实现l2惩罚。
    tol=0.0001, 参数类型：float，默认：e-4。停止优化的错误率
    C=1.0, 参数类型：float，默认；1。正则化强度的导数，值越小强度越大。
    fit_intercept=True, 参数类型：bool，默认：True。确定是否在目标函数中加入偏置。
    intercept_scaling=1, 参数类型：float，默认：1。仅在使用“liblinear”且self.fit_intercept设置为True时有用。
    class_weight=None, 参数类型：dict，默认：None。根据字典为每一类给予权重，默认都是1.
    random_state=None, 参数类型：int，默认：None。在打乱数据时，选用的随机种子。
    solver='warn', 参数类型：str，可选：{'newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'}, 默认：liblinear。选用的优化器。
    max_iter=100, 参数类型：int，默认：100。迭代次数。
    multi_class='warn', 参数类型：str，可选：{'ovr', 'multinomial', 'auto'}，默认：ovr。如果选择的选项是'ovr'，那么二进制问题适合每个标签。对于“多项式”，最小化的损失是整个概率分布中的多项式损失拟合，即使数据是二进制的。当solver ='liblinear'时，'multinomial'不可用。如果数据是二进制的，或者如果solver ='liblinear'，'auto'选择'ovr'，否则选择'multinomial'。
    verbose=0, 参数类型：int，默认：0。对于liblinear和lbfgs求解器，将详细设置为任何正数以表示详细程度。
    warm_start=False, 参数类型：bool，默认：False。是否使用之前的优化器继续优化。
    n_jobs=None，参数类型：bool，默认：None。是否多线程
)