OO第一单元总结
OO第一单元的训练已经全部结束了,从三次作业的训练中锻炼了面向对象思想,下面对三次作业作一些分析和总结。
第一次作业
本次作业是简单多项式的求导,只有幂函数项,相对来说比较简单。
UML图:
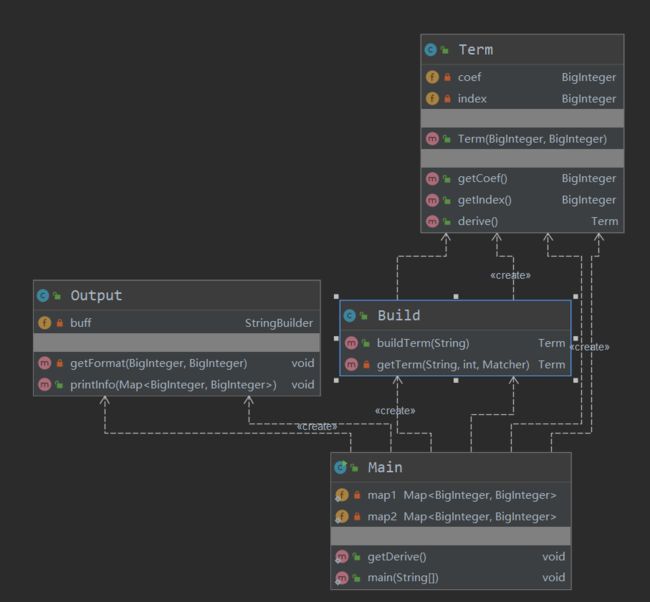
- 总共分为4个类
- Main:主类,接受输入输出
- Term:项,处理幂函数系数、指数及求导规则
- Build:将输入分割成每一项并返回Term对象
- Output:处理求导后多项式的化简及输出
代码行数:
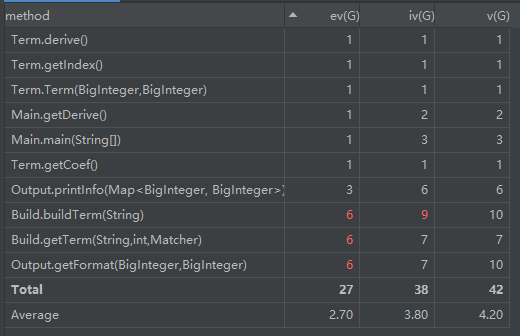
复杂度:
总的来说,本次作业对输入的处理比较简单,不用进行格式检查,所以最终的完成效果比较好,在公测和互测中都未发现bug。性能方面采用hashmap合并同类项,注意1和-1的简化处理就能达到最大形能。
在互测过程中,由于本次的正则表达式并不是非常复杂,所以用python脚本可以随机生成大量的符合要求的数据,来进行测试。
第二次作业
第二次的作业中引入了三角函数,比起第一次作业来讲难度提升还是比较大的。但是项内组合并不复杂,可以为每项归纳出一个通项表示:nx**asin(x)b*cos(x)c。
UML图:
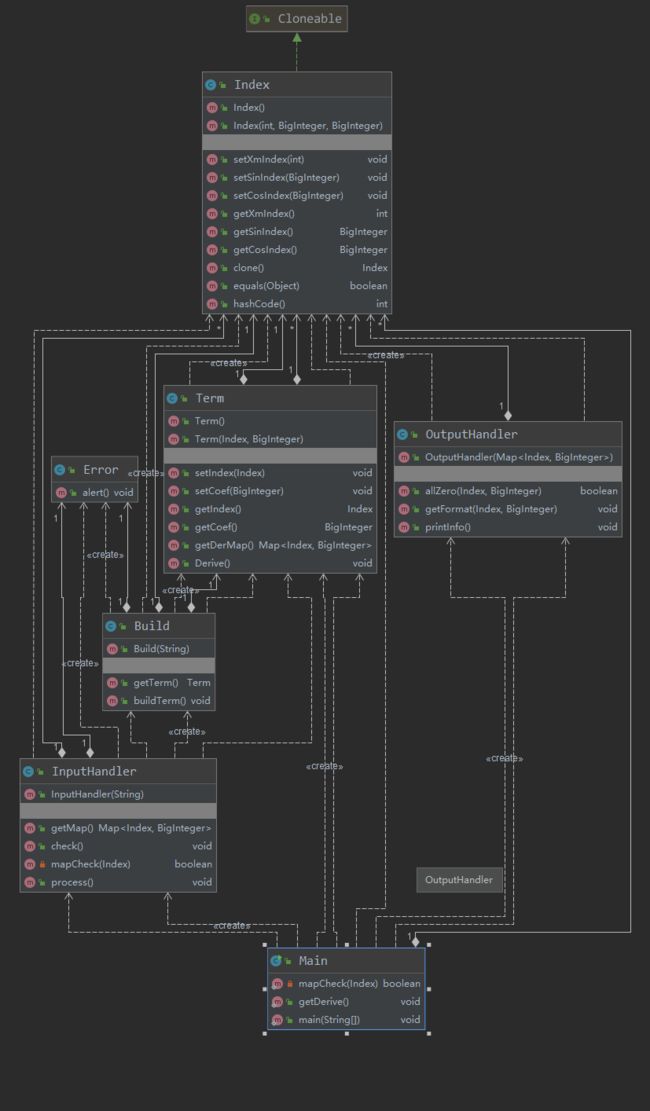
- 总共分为了7个类
- Main:主类,接受输入输出
- InputHandler:输入处理类,检查表达式是否合法,并进行项的分割提取
- Index:指数类,保存通项的三个指数,实现clone接口
- Term:项类,提供求导方法
- Build:相当于工厂模式,输入一个项的字符串,返回一个Term对象
- OutputHandler:优化并处理输出
- Error:错误处理类,在检查到错误格式输出并退出程序
代码行数:
复杂度:
本次作业相对来说难度还是比较大的,主要是在优化方面,三角函数有很大的优化空间,需要利用一些变换来进行项的合并。和第一次作业对比来说,这次作业还是做了比较大的重构了,但是流程模式还是没有发生变化。本次作业另外一个重头戏就是正则表达式的匹配了,这次正则表达式如果按照常规思路来写的话会非常长,自己也不易看懂,出了bug很麻烦。我在构建正则表达式的时候采用了是一种层次构建方法,按照指导书给出的文法,一级一级构建,看起来就比较具有结构性,也比较易读。
在互测阶段被找出有2个bug,一个是由于优化1和-1导致的,在最终的求导项中如果有1或-1的项,只会输出正负号。另一个是求导后合并同类项系数为0的项没有正确输出,在code时忽略了这一点。构建测试样例时,排除一些特殊点,还是可以利用python脚本随机生成表达式。
第三次作业
相对于前两次作业来说,第三次作业难度上有很大的飞跃。新增复合函数、嵌套和表达式因子,并不能为每个项构造一个通项。在表达式的合法性判断和嵌套求导的问题上还存在递归,前两次作业的思想已经不太适用了,对全部代码进行了重构。
UML图:
- 总共分为12个类和一个接口
- Main:主类,接受输入输出
- Derive:求导接口,实现该接口的类必须实现求导方法getDerive()。在设计中,共有7个类实现了该接口,有Constant、Power、Sin、Cos、Multi、Composite、Expression
- Constant:常数类,包括处理每项前的系数
- Power:幂函数类,实现求导方法
- Sin:sin函数类,实现非复合的sin求导
- Cos:cos函数类,实现非复合的cos求导
- Multi:乘法项类,实现乘法求导规则
- Composite:复合函数类,实现复合函数的求导方法
- Expression:表达式因子类,实现表达式因子的处理和求导
- BuildTerm:相当于工厂,对每一项的字符串分类,找到适合的求导法则
- DeriveProcess:求导入口,对项表逐项求导
- InputHandler:输入处理类,实现输入表达式的合法性判断并分割表达式的每项,调用BuildTerm进行处理,并调用DeriveProcess进行每项的求导
- Error:错误处理类,输出报错信息并退出程序
代码行数:
复杂度:
本次作业的难度可以说是非常大的。就我个人来说,我认为难度主要集中在以下三点:
一、表达式的合法性判断。由于本次的表达式文法存在着递归定义的问题,直接用正则表达式是不可行的,存在正则自己调用自己的问题。参考了作业讨论区同学分享的一些可行方法之后,我的实现方法就是把sin和cos括号中的全部内容用'@'替换,识别到表达式因子是,把整个表达式因子(带括号)用'#'替换,再构造正则表达式去实现匹配检查,同时也要对'@'和'#'代表的因子进行格式检查,递归进行。
二、求导规则的识别问题。我并没有建立表达式树,在我的设计中,我需要为表达式的每一项寻找到一种求导规则。在实现这部分功能的过程中,乘法项、复合项和表达式因子项由于括号的关系,造成这三点比较难以识别,在互测中的一个bug也是由于这部分功能存在缺陷导致的。
三、优化问题。这一次的优化难度也很大,也有不少同学栽在了自己优化埋下的坑中。
在这次作业的公测和互测中共被发现3个bug。1、cos(- 1)有非法空白字符没有识别出来。这一部分和自己设计的格式检查流程有关。我是先检查非法字符,即不应该在表达式中出现的字符。其次是检查空白字符,我并没有将空白字符写入正则表达式中,采用枚举所有空白字符的非法情况如下:
String wrongBlank1 = "((\\*[ \\t]+\\*)|([ \\t]+[io])|([io][ \\t]+))";
String wrongBlank2 = "((\\d[ \\t]+\\d)|(\\*{1,2}[ \\t]*[+-][ \\t]+\\d))";
String wrongBlank3 = "(([+-][ \\t]*[+-][ \\t]*[+-][ \\t]+\\d+)|([ns]\\([+-][ \\t]+\\d))";
然后检查指数,最后对整个表达式替换递归检查。2、在常数项求导的处理上,也是由于优化造成的输出结果非法。3、之前说过的求导规则的识别上。
在这次互测中,就全部采用的手动构造测试样例的方法了。构造多个测试样例,通过脚本运行多个程序输出结果然后只能观察结果是否复合预期了。
总结及心得体会
1、程序扩展性的问题
这一单元的作业前2次比较简单,在构造程序结构的时候并没有想那么多,在第三次作业难度提升起来后,在架构的设计上就花费了非常多的时间,重构了全部的代码,也由于此原因在中测时通过评测机返回的信息不停的debug,发现了各种低级bug。
2、对比体会
在这样的一个互测模式下,通过三次互测也见到了20多位其他同学的代码,有见过写得比较好的(包多类多),也见过第三次作业也一main到底和完全面向过程的程序。第三次作业自己的代码数比较多达到了900多行,却没有实现多少优化,反思其原因,还是由于自己的设计模式还是不够好,很多类中都有大量功能相似的方法,包括在每个方法中,可能用正则匹配多次的时候,也没有抽象出函数来写。从这几次作业中发现作业讨论区也是一个好东西,自己作业设计的灵感也有部分来源于那。
3、总结
总而言之,第一单元已经结束了,整体来看,三次作业的完成情况应该还算是可以,把自己和之前对比,还是学到了不少东西,对java语言本身也了解得更多。马上进入到第二单元,希望自己在第二单元的时候,能有更好的设计和扩展性,不要一次次重构,一次次de重构代码的bug。