逻辑回归
逻辑回归介绍
逻辑回归是一种广义线性回归,本质上与多元线性回归相差无几。相当于将回归的结果带入 sigmoid 函数进行缩放,使得最终结果为二分类
原理与预测函数
 预测函数,拿我们讨论的最标准的二分类来说,分别计算p(y=1|x),p(y=0|x)哪个条件概率大就分到哪一类
预测函数,拿我们讨论的最标准的二分类来说,分别计算p(y=1|x),p(y=0|x)哪个条件概率大就分到哪一类
损失函数的推导
反映了两个概率分布之间的差异信息,其中p表示真实分布,q表示非真实分布,即反应我们推测的分布和真实分布的差异大小信息
逻辑回归的代价函数
正确率与召回率
召回率(Recall) = 系统检索到的相关文件 / 系统所有相关的文件总数
正确率(Precision) = 系统检索到的相关文件 / 系统所有检索到的文件总数
梯度下降法实现逻辑回归
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn import preprocessing
scale = True
# 导入数据
data = np.genfromtxt('D:/数据/逻辑回归.txt', delimiter=',',encoding='utf-8')
'''
# data = pd.read_table('D:/数据/逻辑回归.txt', sep=',')
# 将数据转化为矩阵形式
data_1 = data.values
# 将数据转化为array
data_2 = np.array(data_1)
'''
# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
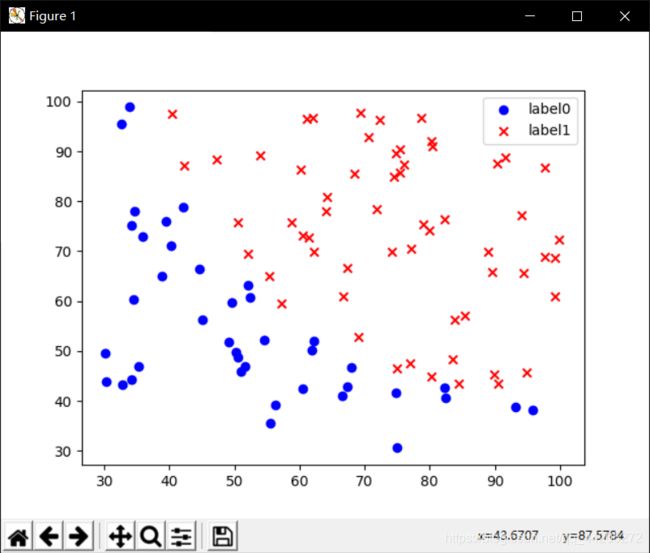
# 画出散点图
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类型的数据
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append((x_data[i, 1]))
else:
x1.append(x_data[i, 0])
y1.append((x_data[i, 1]))
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
# 画图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
# plot()
# 数据处理,添加偏置项
x_data = data[:, :-1]
y_data = data[:, -1, np.newaxis]
# 如果输入本身就是一个矩阵,则np.mat不会对该矩阵make a copy.仅仅是创建了一个新的引用。相当于np.matrix(data, copy = False)
print(np.mat(x_data).shape)
print(np.mat(y_data).shape)
# 给样本添加偏置项
# 数组拼接
X_data = np.concatenate((np.ones((100, 1)), x_data), axis=1)
# print(X_data)
print(X_data.shape)
def sigmoid(x):
return 1.0/(1 + np.exp(-x))
def cost(xmat, ymat, ws):
# multiply是对应元素相乘
left = np.multiply(ymat, np.log(sigmoid(xmat*ws)))
right = np.multiply(1-ymat, np.log(1-sigmoid(xmat*ws)))
return np.sum(left+right) / -(len(xmat))
def graAscent(xarr, yarr):
if scale == True:
xarr = preprocessing.scale(xarr)
xmat = np.mat(xarr)
ymat = np.mat(yarr)
# 设置学习率
lr = 0.001
# 设置迭代的次数
epochs = 10000
# 保存代价函数的值
costlist = []
# 计算数据行列数
# 行代表数据个数,列代表权值个数
m, n = np.shape(xmat)
ws = np.mat(np.ones((n, 1)))
for i in range(epochs+1):
# xmat与ws矩阵相乘
h = sigmoid(xmat*ws)
# 计算误差
ws_grad = xmat.T*(h - ymat) / m
ws = ws - lr*ws_grad
if i % 50 == 0:
costlist.append(cost(xmat, ymat, ws))
return ws, costlist
# 训练模型,得到权值和cost的变化
ws, costlist = graAscent(X_data, y_data)
print(ws)
# 画决策边界
if scale == False:
plot()
x_test = [[100], [30]]
y_test = (-ws[0][0]-x_test*ws[1][0]) / ws[2][0]
plt.plot(x_test, y_test, 'k')
plt.show()
''
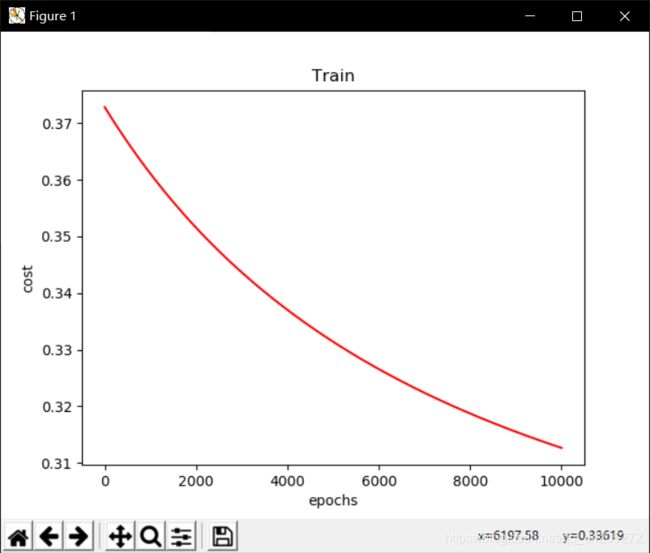
# 画loss图的变化
x = np.linspace(0, 10000, 201)
plt.plot(x, costlist, c='r')
plt.title('Train')
plt.xlabel('epochs')
plt.ylabel('cost')
plt.show()
# 预测
def predict(x_data, ws):
if scale==True:
x_data = preprocessing.scale(x_data)
xmat = np.mat(x_data)
ws = np.mat(ws)
return [1 if x >= 0.5 else 0 for x in sigmoid(xmat*ws)]
predictions = predict(X_data, ws)
# 计算正确率与召回率
print(classification_report(y_data, predictions))
'''
precision recall f1-score support
0.0 0.78 0.95 0.85 40
1.0 0.96 0.82 0.88 60
accuracy 0.87 100
macro avg 0.87 0.88 0.87 100
weighted avg 0.89 0.87 0.87 100
'''
loss图像
sklearn 实现逻辑回归
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn import linear_model
scale = True
# 导入数据
data = np.genfromtxt('D:/数据/逻辑回归.txt', delimiter=',',encoding='utf-8')
'''
# data = pd.read_table('D:/数据/逻辑回归.txt', sep=',')
# 将数据转化为矩阵形式
data_1 = data.values
# 将数据转化为array
data_2 = np.array(data_1)
'''
# 切分数据
x_data = data[:, :-1]
y_data = data[:, -1]
# 画出散点图
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类型的数据
for i in range(len(x_data)):
if y_data[i] == 0:
x0.append(x_data[i, 0])
y0.append((x_data[i, 1]))
else:
x1.append(x_data[i, 0])
y1.append((x_data[i, 1]))
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
# 画图例
plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
# plot()
# 建立逻辑回归模型
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
if scale == True:
plot()
x_test = np.array([[100], [30]])
y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0]) / logistic.coef_[0][1]
plt.plot(x_test, y_test, 'k')
plt.show()
predictions = logistic.predict(x_data)
print(classification_report(y_data, predictions))
'''
precision recall f1-score support
0.0 1.00 0.68 0.81 40
1.0 0.82 1.00 0.90 60
accuracy 0.87 100
macro avg 0.91 0.84 0.85 100
weighted avg 0.89 0.87 0.86 100
'''