第八十二篇 机器学习（介绍）

心得：终于决定要踏上了新的旅程，一个全新的领域等待着你去挑战，你知道你的内心有许多不甘心，所以 拼一次~

一、机器学习相关概念

1. 什么是人工智能

它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
人工智能是研究使计算机来模拟人的某些思维过程和智能行为（如学习、推理、思考、规划等）的学科，主要包括计算机实现智能的原理、制造类似于人脑智能的计算机，使计算机能实现更高层次的应用。
主要解决如：自然语言理解，图像识别，语音识别等问题

2. 什么是机器学习

机器学习是一种能够赋予机器学习的能力以此让它完成直接编程无法完成的功能的方法。但从实践的意义上来说，机器学习是一种通过利用数据，训练出模型，然后使用模型预测的一种方法。

3. 什么是深度学习

深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向
深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。 深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。

4.什么是人工神经网络

神经网络起源于对生物神经元的研究，如下图所示生物神经元包括细胞体，树突，轴突等部分。其中树突是用于接受输入信息，输入信息经过突触处理，当达到一定条件时通过轴突传出，此时神经元处于激活状态；反之没有达到相应条件，则神经元处于抑制状态。

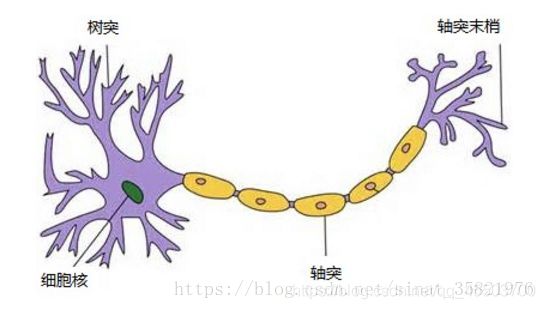
人工神经网络

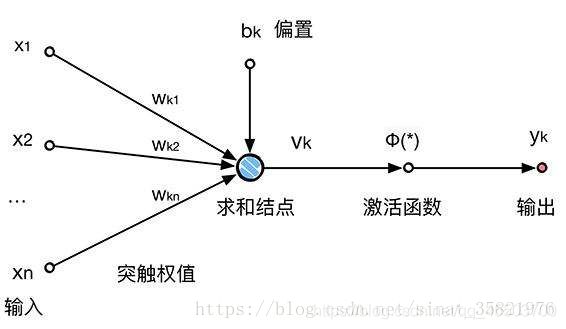
对应关系

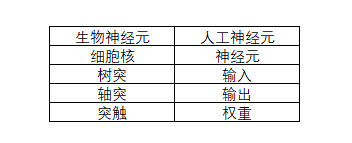
由大量的人工神经元互相连接而形成的复杂网络结构成为人工神经网络

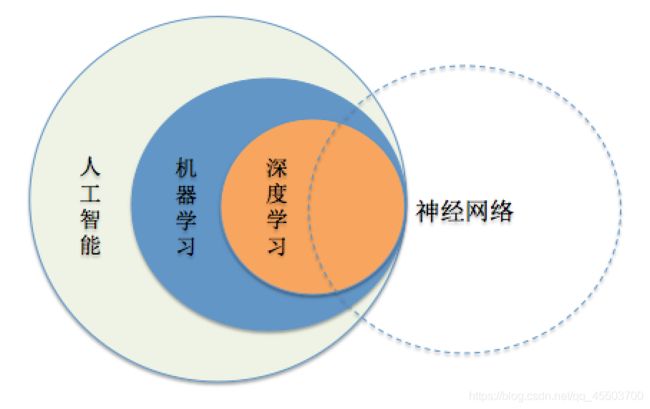
5.它们之间的关系

二、机器学习分类

小结

监督学习：
In：有标签
Out：有反馈
目的：预测结果
案例：学认字
算法：分类（类别），回归（数字）

无监督学习：
In：无标签
Out：无反馈
目的：发现潜在结构
案例：自动聚类
算法：聚类，降维

半监督学习:
已知：训练样本Data和待分类的类别
未知：训练样本有无标签均可
应用：训练数据量过时，
监督学习效果不能满足需求，因此用来增强效果。

强化学习：
In：决策流程及激励系统
Out：一系列行动
目的：长期利益最大化，回报函数（只会提示你是否在朝着目标方向前进的延迟反映）
案例：学下棋
算法：马尔科夫决策，动态规划

1. 监督学习（Supervised learning）

给定训练样本，每个输入x对应一个确定结果Y,我们需要训练出一个模型，在未知样本x给定后，对Y进行预测。给算法一个数据集，其中数据集中包含了“正确答案”，根据这些样本做出算法预测，得到未知数据的“正确答案”。
概况为两类：回归问题和分类问题

1. 回归问题：离散数据集—连续输出
   如房价预测，根据离散样本集拟合出一条连续曲线，得到房子的“估价”
2. 分类问题
   例如：根据肿瘤特征组（可以为多个或无限个特征）判断良性还是恶性，得到的是结果是“良性”或者“恶性”，是离散的。此外，在用大数量的特征做预测时，你的计算机可能会溢出，如何处理无个特征？

有监督学习：对具有概念标记（分类）的训练样本进行学习，以尽可能对训练样本集外的数据进行标记（分类）预测。这里，所有的标记（分类）是已知的。因此，训练样本的岐义性低

优点：泛化错误率低，结果易解释。

缺点：对大规模训练样本难以实施，解决多分类问题存在困难，对参数调节和核函数的选择敏感。

应用场景：文本分类、人像识别、医学诊断等。

2.非监督学习

非监督学习的数据集跟监督学习的数据集不同，它没有任何标签，即没有相应的“正确答案”。 非监督学习指，给出一组无标签的数据集，通过学习而得到数据的某种结构。

聚类问题：可能判定数据为两个不同的聚集簇，称为聚类算法。（聚类算法应用较广，如GOOGLE NEWS）

无监督学习：对没有概念标记（分类）的训练样本进行学习，以发现训练样本集中的结构性知识。这里，所有的标记（分类）是未知的。因此，训练样本的岐义性高。聚类就是典型的无监督学习。

3.半监督学习

是监督学习与无监督学习相结合的一种学习方法。半监督学习使用大量的未标记数据，以及同时使用标记数据，来进行模式识别工作。

4.强化学习

以环境反惯(奖/惩信号)作为输入，以统计和动态规划技术为指导的一种学习方法。没有标注数据集，通过回报函数判定是否越来越接近目标。

5.推荐系统

推荐系统有3个重要的模块：用户建模模块、推荐对象建模模块、推荐算法模块。通用的推荐系统模型流程如图。推荐系统把用户模型中兴趣需求信息和推荐对象模型中的特征信息匹配，同时使用相应的推荐算法进行计算筛选，找到用户可能感兴趣的推荐对象，然后推荐给用户。

三、机器学习常用算法

大概介绍一下各类算法，在之后的文章中会逐一对算法进行分析学习

1. 线性回归

线性回归的表示是一个方程，它描述了一条线，通过寻找输入变量系数(B)的特定权重，拟合输入变量(x)和输出变量(y)之间的关系。

例如：y=B0+B1∗x
我们将在给定输入x的情况下预测y，线性回归学习算法的目标是找到系数B0和B1的值。 可以使用不同的技术从数据中学习线性回归模型，如普通最小二乘的线性代数解和梯度下降优化。

2. 逻辑回归(logistic regression)

面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。
Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）
回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率

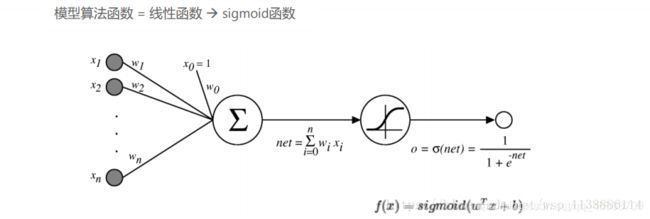
通过训练数据x来计算出向前传播成本cost，计算向后传播对应的导数,dw,db，通过迭代来更新参数w,b，来训练出一个契合数据的模型。

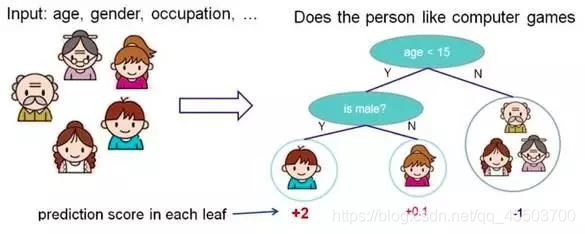
3. 决策树

根据一些 feature（特征） 进行分类，每个节点提一个问题，通过判断，将数据分为两类，再继续提问。这些问题是根据已有数据学习出来的，再投入新数据的时候，就可以根据这棵树上的问题，将数据划分到合适的叶子上。需要注意的是，在给定特征时，那个特征先输入，得根据此特征值的熵来决定。熵越大的信息量越大，用它先分割效果会更好。

4. 聚类

聚类(clustering)是一种无监督学习(unsupervised learning)，即没有标记信息，通过对无标记训练样本的学习发现数据的内在性质和规律。

K-means算法：

算法步骤：
(1) 首先我们选择一些类/组，并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。
(2) 计算每个数据点到中心点的距离，数据点距离哪个中心点最近就划分到哪一类中。
(3) 计算每一类中中心点作为新的中心点。
(4) 重复以上步骤，直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点，然后选择运行结果最好的一个。

5. 朴素贝叶斯

在已知场景发生的概率来推断未知场景的概率


例子：

应用场景：

6. k近邻算法(knn)

监督学习：

给一个新的数据时，离它最近的k个点中，那个类别多，这个数就属于哪一类（算距离，找k个邻居，计算出分类）

如下：当k=1时，？属于红色方框；当k=5时，？属于灰色三角形。


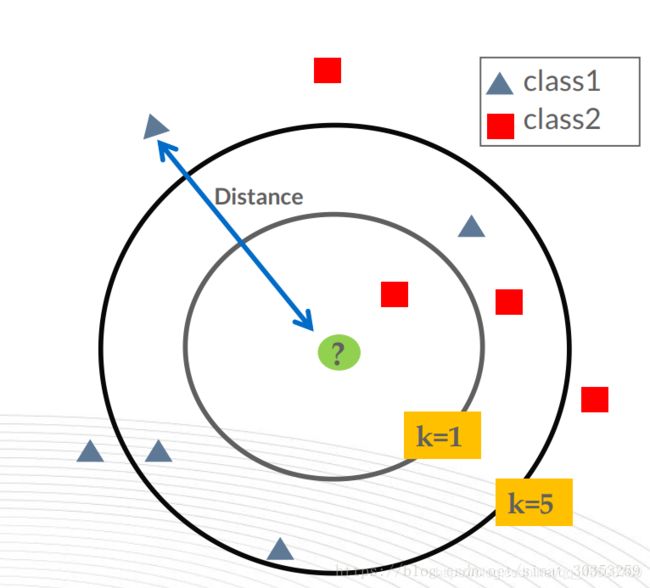
k值选择一般低于训练样本数的平方根

7. SVM

将实例的特征向量（以二维为例）映射为空间中的一些点，就是如下图的实心点和空心点，它们属于不同的两类。

那么 SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

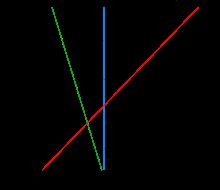
能够画出多少条线对样本点进行区分？
：线是有无数条可以画的，区别就在于效果好不好。

比如绿线就不好，蓝线还凑合，红线看起来就比较好。
我们所希望找到的这条效果最好的线叫作划分超平面

为什么要叫作“超平面”呢？
：因为样本的特征很可能是高维的，此时样本空间的划分就需要“超平面”。

画线的标准是什么？/ 什么才叫这条线的效果好？
：SVM 将会寻找可以区分两个类别并且能使边际（margin）最大的超平面（hyper plane），即划分超平面。

8. 集成算法

简单算法一般复杂度低，速度快，易展示结果，但预测效果往往不是特别好。每种算法好像一种专家，集成就是把简单的算法（后文称基算法/基模型）组织起来，即多个专家共同决定结果。

集成算法一般分为三类：Bagging，Boosting，Stacking（我们可以把它简单地看成并行，串行和树型）。Bagging是把各个基模型的结果组织起来，取一个折中的结果；Boosting是根据旧模型中的错误来训练新模型，层层改进；Stacking是把基模型组织起来，注意不是组织结果，而是组织基模型本身，该方法看起来更灵活，也更复杂。

9. CNN(卷积神经网络)

CNN的目的：特征提取，减少复杂度
层次：卷积层 .池化层 .输出层

Convolution 卷积层：利用局部特征（卷积核），去计算出目标的 整体特征情况。
根据权重黄色区域依次扫描图片数据，得出具备特征的卷积数据

Pooling Layer池化层
具体的Pooling有两种，取平均值（mean）和取最大值（max）,下图是取最大值

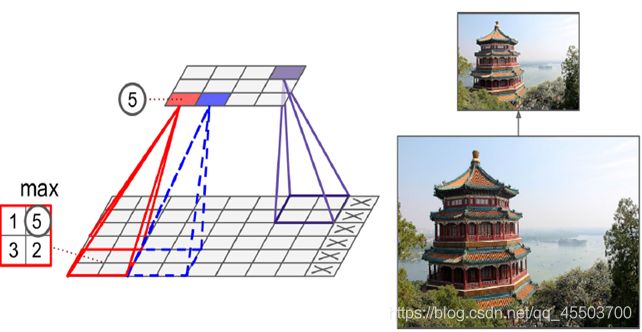
10. BP算法

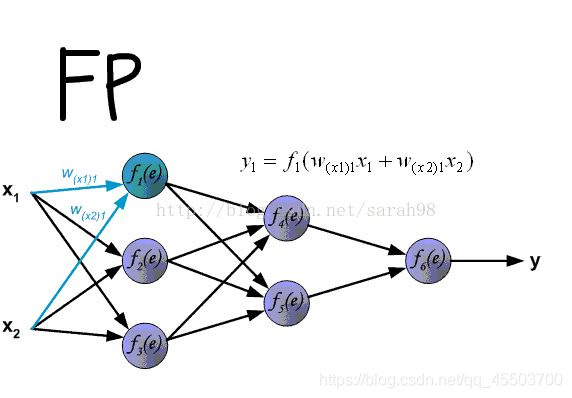
BP神经网络学习过程由信息的下向传递和误差的反向传播两个过程组成

正向传递：由模型图中的数据x从输入层到最后输出层z的过程。

反向传播：在训练阶段，如果正向传递过程中发现输出的值与期望的传有误差，由将误差从输出层返传回输入层的过程。返回的过程主要是修改每一层每个连接的权值w，达到减少误的过程。

四、专有名词介绍

1 熵

熵是来定义混乱的，熵越小，这个时候就最有秩序，而被打乱时，熵就开始增大，最后一篇混乱，变为最大。

熵增原理：宇宙中事物都有自发变得混乱的倾向，也就是说熵会不断增加；比如卧室不收拾会越来越乱；年久失修的建筑物逐渐破败

可能的熵：100个可以放置物品的位置，20个物品放在合适的位置，整洁的概率p为
p=C(100,20)=100!/20!*80! =5.38*10^20

C(n,m) 从n中选出m个的组合 =n!/m!*(n-m)!
A(n,m)从n中选出m个不同顺序 = n*n(-1)*(n-2)…*(n-m+1)

所以熵越大，不确定性就越大，比如应用到语言中，在一本英文和一本中文书面前，中文书明显薄，能用简易的词语描绘出事情本身，这也就说明，同一句话，中文所包含的信息越多，熵越大

2 线性

两个变量之间的关系是一次函数关系的——图象是直线，叫做线性。
注意：题目的线性是指广义的线性，也就是数据与数据之间的关系。

3 非线性

两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。

相信通过以上两个概念大家已经很清楚了，其次我们经常说的回归回归到底是什么意思呢。

4 回归

人们在测量事物的时候因为客观条件所限，求得的都是测量值，而不是事物真实的值，为了能够得到真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。
通俗的说就是用一个函数去逼近这个真实值，那又有人问了，线性回归不是用来做预测吗？是的，通过大量的数据我们是可以预测到真实值的。